优化绝技-梯度下降(Gradient Descent)

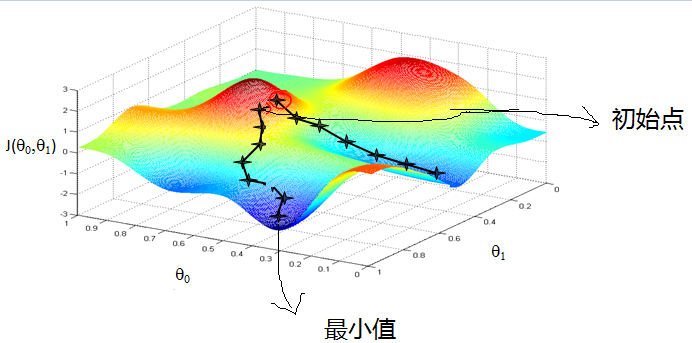
在线性模型中, 我们除了使用最小二乘法 (或者称为正规方程法), 我们还可以使用一种常用的凸优化技术: 梯度下降! 它的主要目的是通过迭代找到目标函数的最小值,

梯度下降法的基本思想可以类比为一个下山的过程.

假设这样一个场景: 一个人被困在山上, 需要从山上下来(找到山的最低点, 也就是山谷). 但此时山上的浓雾很大, 导致可视度很低; 因此, 下山的路径就无法确定, 必须利用自己周围的信息一步一步地找到下山的路. 这个时候, 便可利用梯度下降算法来帮助自己下山. 怎么做呢? 首先以他当前的所处的位置为基准, 寻找这个位置最陡峭的地方, 然后朝着下降方向走一步, 然后又继续以当前位置为基准, 再找最陡峭的地方, 再走直到最后到达最低处; 同理上山也是如此, 只是这时候就变成梯度上升算法了.

从上面的解释可以看出, 梯度下降不一定能够找到全局的最优解, 有可能是一个局部最优解. 当然, 如果损失函数是严格凸函数, 梯度下降法得到的解就一定是全局最优解.

梯度下降的基本过程就和下山的场景很类似. 根据之前的场景假设, 最快的下山的方式就是找到当前位置最陡峭的方向, 然后沿着此方向向下走, 对应到函数中, 就是找到给定点的梯度, 然后朝着梯度相反的方向, 就能让函数值下降的最快! 因为梯度的方向就是函数之变化最快的方向.

1. Why Gradient?

所以, 我们重复利用这个方法, 反复求取梯度, 最后就能到达局部的最小值, 这就类似于我们下山的过程. 而求取梯度就确定了最陡峭的方向, 也就是场景中测量方向的手段. 那么为什么梯度的方向就是最陡峭的方向呢? 接下来, 我们从微分开始讲起.

看待微分的意义, 可以有不同的角度, 最常用的两种是:

• 函数图像中, 某点的切线的斜率
• 函数的变化率

单变量微分我们这里就不介绍了, 主要看一下多变量微分. 当函数有多个变量的时候, 即分别对每个变量进行求微分. 梯度实际上就是多变量微分的一般化. 这里以二元函数 $z=f(x,y)$ 为例讲解偏导数, 其余情况以此类推.

由于二元函数具有两个自变量 $(x,y)$, 因此函数图像为一个曲面. 与一元函数类似, 如何计算二元函数对曲面上一点 $(x_0,y_0)$ 的变化率呢? 此处需要注意的是, 因为过曲面上一点可以作出无数条切线, 因此函数在该点也具有无数个变化率. 为了简单起见, 可以先考虑函数沿着两个坐标轴 $x$ 轴和 $y$ 轴方向的变化率.

• 当自变量 $y$ 固定在 $y_0$, 函数在点 $x_0$ 处的变化率称为函数在点 $(x_0,y_0)$ 处对 $x$ 的偏导数, 记作 $f_x(x_0,y_0)$;
• 当自变量 $x$ 固定在 $x_0$, 函数在点 $y_0$ 处的变化率称为函数在点 $(x_0,y_0)$ 处对 $y$ 的偏导数, 记作 $f_y(x_0,y_0)$;

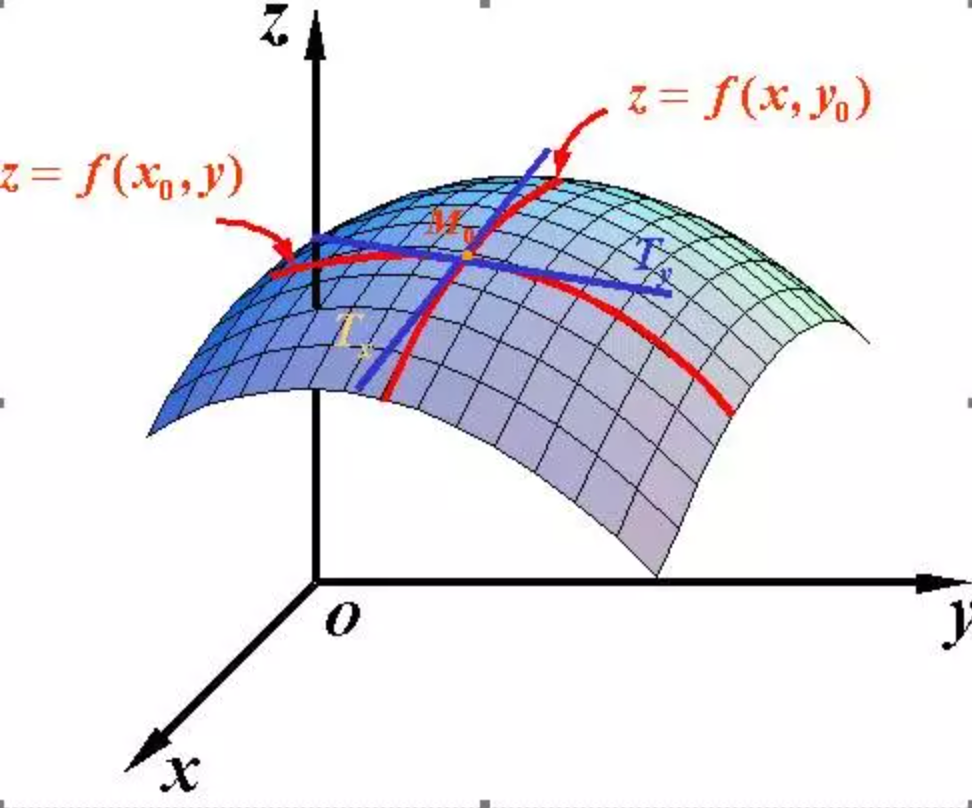
可能到这里, 读者就已经发现偏导数的局限性了, 原来我们学到的偏导数指的是多元函数沿坐标轴的变化率, 但是我们往往很多时候要考虑多元函数沿任意方向的变化率, 那么就引出了方向导数.

因此, 如何求出函数在点 $(x_0,y_0)$ 处沿某一方向的变化率呢? 万变不离其宗, 此时仍然按照变化率的定义去求解, 即只需求出函数的增量与自变量沿着某一方向增量比值的极限即可.

假设某一方向的单位向量为 $e_l=(\cos\alpha,\sin\alpha)$, $\alpha$ 为此向量与 $x$ 轴正向夹角. 显然, $\alpha$ 不同, 此向量能够表示任意方向的单位向量. 当点 $(x_0,y_0)$ 沿着该方向产生一个增量 $t$ 到达点 $(x_0+t\cos\alpha,y_0+t\sin\alpha)$ 时, 函数 $z$ 也会产生一个增量 $\triangle z=f(x_0+t\cos\alpha,y_0+t\sin\alpha)-f(x_0,y_0)$, 此时函数沿此方向的变化率为

$$\lim\limits_{t\rightarrow0^+}\frac{f(x_0+t\cos\alpha,y_0+t\sin\alpha)-f(x_0,y_0)}{t}=f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\sin\alpha$$

在了解了多元函数的方向导数之后, 一个很自然的问题是: 既然函数在点 $(x_0,y_0)$ 处沿着任意的方向都有一个变化率, 那么沿着哪个方向 ($\alpha=?$) 函数的变化率最大呢?

根据上面的推导, 我们知道函数 $z=f(x,y)$ 沿着任意方向 ($\alpha$ 取任意值) 的变化率为

$$f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\sin\alpha$$

因此接下来只需求得使其达到最大值时的 $\alpha$ 便可以解决上诉问题. 由于上式可以看成两个向量的内积, 令

$$\mathbf{g}=(f_x(x_0,y_0),f_y(x_0,y_0)) \\ \mathbf{e}_l=(\cos\alpha,\sin\alpha)$$

则

$$f_x(x_0,y_0)\cos\alpha+f_y(x_0,y_0)\sin\alpha=\mathbf{g}\cdot\mathbf{e}_l=|\mathbf{g}||\mathbf{e}_l|\cos\theta=|\mathbf{g}|\cos\theta$$

其中, $\theta$ 为 $\mathbf{g}$ 和 $\mathbf{e}_l$ 的夹角, 根据上式, 我们可以得出结论:

• 当 $\theta=0$, 即 $\mathbf{g}$ 和 $\mathbf{e}_l$ 方向相同时, 函数的变化率最大, 且在点 $(x_0,y_0)$ 呈上升趋势;
• 当 $\theta=\pi$, 即 $\mathbf{g}$ 和 $\mathbf{e}_l$ 方向相反时, 函数的变化率最大, 且在点 $(x_0,y_0)$ 呈下降趋势;

最后, 当点 $(x_0,y_0)$ 确定后, 向量 $\mathbf{g}$ 也随之确定. 由于向量 $\mathbf{g}$ 的方向为函数值增加最快的方向, 而此方向经常被用于实际生活中, 因此为便于表述, 人们为其取了一个名字—梯度. 换而言之, 多元函数在某一点的梯度是一个非常特殊的向量, 其由多元函数对每个变量的偏导数组成 (这即是为什么求梯度的时候需要对各个变量求偏导的原因), 其方向为函数在该点增加最快的方向, 大小为函数在该点的最大变化率.

2. Example

2.1 Single Variable

我们首先给出数学公式: $\theta_1=\theta_0-\alpha\triangledown\mathbf{J}(\theta)$

此公式的意义是: $\mathbf{J}$ 是关于 $\theta$ 的一个函数, 我们当前所处的位置为 $\theta_0$ 点, 要从这个点走到 $\mathbf{J}$ 的最小值点, 也就是山底. 首先我们先确定前进的方向, 也就是梯度的反向, 然后走一段距离的步长, 也就是 $\alpha$, 走完这个段步长, 就到达了 $\theta_1$ 这个点!

$\alpha$ 在梯度下降算法中被称作为学习率或者步长, 意味着我们可以通过 $\alpha$ 来控制每一步走的距离, 以保证不要步子跨的太大扯着蛋, 哈哈, 其实就是不要走太快, 错过了最低点. 同时也要保证不要走的太慢, 导致太阳下山了, 还没有走到山下. 所以 $\alpha$ 的选择在梯度下降法中往往是很重要的!

注:

梯度前加一个负号, 就意味着朝着梯度相反的方向前进! 我们在前文提到, 梯度的方向实际就是函数在此点上升最快的方向! 而我们需要朝着下降最快的方向走, 自然就是负的梯度的方向, 所以此处需要加上负号; 那么如果时上坡, 也就是梯度上升算法, 当然就不需要添加负号了.

我们利用上述的数学公式来看一个个简单的梯度下降的例子. 我们假设有一个单变量的函数

$\mathbf{J}(\theta)=\theta^2$

函数的微分, 直接求导就可以得到

$\mathbf{J}’(\theta)=2\theta$

初始化, 也就是起点, 起点可以随意的设置, 这里设置为1

$\theta_0=1$

学习率也可以随意的设置, 这里设置为0.4

$\alpha=0.4$

根据梯度下降的计算公式

$\theta_1=\theta_0-\alpha\triangledown\mathbf{J}(\theta)$

我们开始进行梯度下降的迭代计算过程

如图, 经过四次的运算, 也就是走了四步, 基本就抵达了函数的最低点, 也就是山底

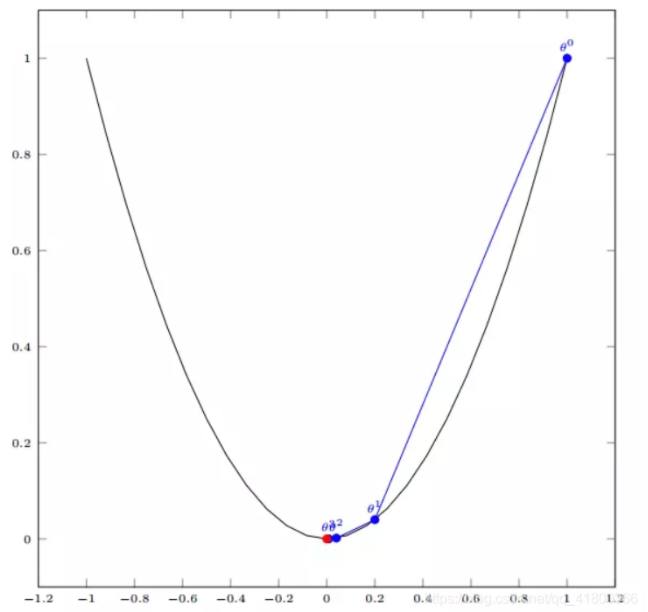
2.2 Multi Varibles

我们假设有一个目标函数

$\mathbf{J}(\theta)=\theta_1^2+\theta_2^2$

现在要通过梯度下降法计算这个函数的最小值. 我们通过观察就能发现最小值其实就是 (0, 0)点. 但是接下来, 我们会从梯度下降算法开始一步步计算到这个最小值!

我们假设初始的起点为

$\theta_0=(1,3)$

初始的学习率为

$\alpha=0.1$

函数的梯度为

$\triangledown\mathbf{J}(\theta)=<2\theta_1,2\theta_2>$

进行多次迭代

我们此时注意到, 在更新 $\theta$ 的时候, 我们是同步更新. 具体来说, 我们在这里有两个参数, 我们是同步更新的, 而不是先计算其中一个参数然后用这个新的值去计算另外一个参数.

我们发现，已经基本靠近函数的最小值点

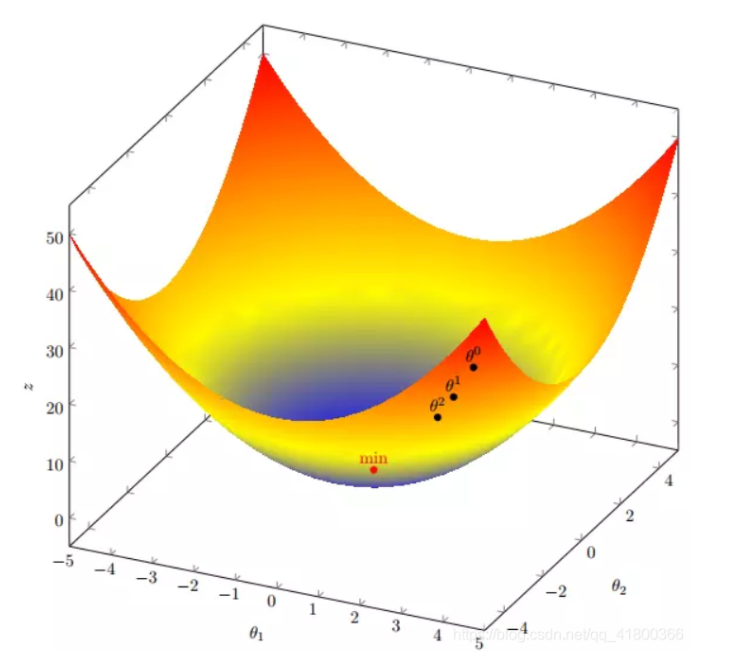
2.3 Linear Regression

我们用 Python 来实现一个简单的梯度下降算法. 场景是一个简单的线性回归的例子: 假设现在我们有一系列的点, 如下图所示

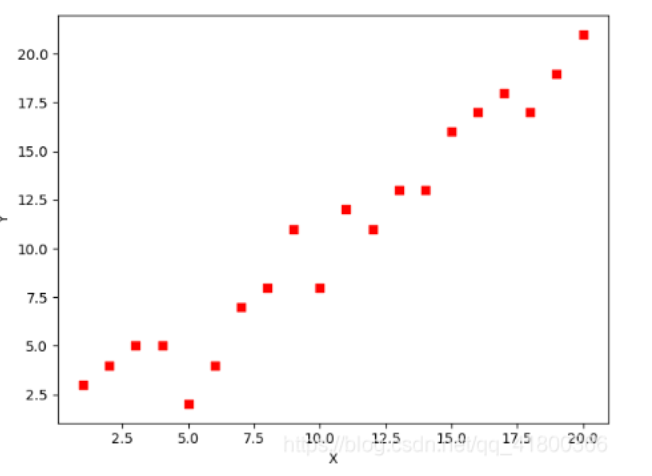
首先, 我们需要定义一个代价函数, 在此我们选择均方误差代价函数

$\mathbf{J}(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)})^2$

此公式中:

• m是数据集中数据点的个数, 也就是样本数;

• $\frac{1}{2}$ 是一个常量, 这样是为了在求梯度的时候, 二次方乘下来的 2 就和这里的 $\frac{1}{2}$ 抵消了, 自然就没有多余的常数系数, 方便后续的计算, 同时对结果不会有影响;

• $y$ 是数据集中每个点的真实 $y$ 坐标的值, 也就是类标签;

• $h$ 是我们的预测函数 (假设函数), 根据每一个输入$x$, 根据 $\theta$ 计算得到预测的 $y$ 值, 即

  $h_{\theta}(x^{(i)})=\theta_0+\theta_1x^{(i)}$

我们可以根据代价函数看到, 代价函数中的变量有两个, 所以是一个多变量的梯度下降问题, 求解出代价函数的梯度, 也就是分别对两个变量进行微分

$$\triangledown\mathbf{J}(\theta)=<\frac{\delta\mathbf{J}}{\delta\theta_0},\frac{\delta\mathbf{J}}{\delta\theta_1}> \\ \frac{\delta\mathbf{J}}{\delta\theta_0}=\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)}) \\ \frac{\delta\mathbf{J}}{\delta\theta_1}=\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)})x^{(i)}$$

根据, 我们之前在线性回归 Normal Equation Method 那里所提到的, 我们可以将目标函数和以及其梯度给转换成矩阵形式

$$\mathbf{J}(\theta)=\frac{1}{2m}(X\Theta-\overrightarrow{y})^T(X\Theta-\overrightarrow{y}) \\ \triangledown\mathbf{J}(\theta)=\frac{1}{m}X^T(X\Theta-\overrightarrow{y})$$

代码如下:

# 这其实是一个 batch gradient descent
import numpy as np

# 数据集大小, 即 20 个数据点
m = 20
# Design Matrix
x0 = np.ones((m,1))
x1 = np.arange(1,m+1).reshape(m,1)
X = np.hstack((x0,x1))
# 对应的 y 
y = np.array([
    3,4,5,5,2,4,7,8,11,8,12,
    11,13,13,16,17,18,17,19,21
]).reshape(m,1)
# 学习率
alpha = 0.01

# 定义代价函数
def cost_function(theta,X,y):
    diff = np.dot(X,theta) - y
    return (1/2*m) * np.dot(diff.T,diff)

# 定义代价函数对应的梯度函数
def gradient_function(theta,X,y):
     diff = np.dot(X,theta) - y
     return 1/m * np.dot(X.T,diff)

# 梯度下降迭代
def gradient_descent(X,y,alpha):
    theta = np.array([1,1]).reshape(2,1)
    gradient = gradient_function(theta,X,y)
    while not all(abs(gradient) <= 1e-5):
        theta = theta - alpha*gradient
        gradient = gradient_function(theta,X,y)
    return theta

3. Algorithm

一般线性回归函数的假设函数为

$$h_{\theta}=\sum_{j=0}^n\theta_jx_j$$

对应的损失函数形式为

$$J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x_i)-y_i)^2$$

下图为一个二维参数 $(\theta_0,\theta_1)$ 组对应损失函数的可视化图

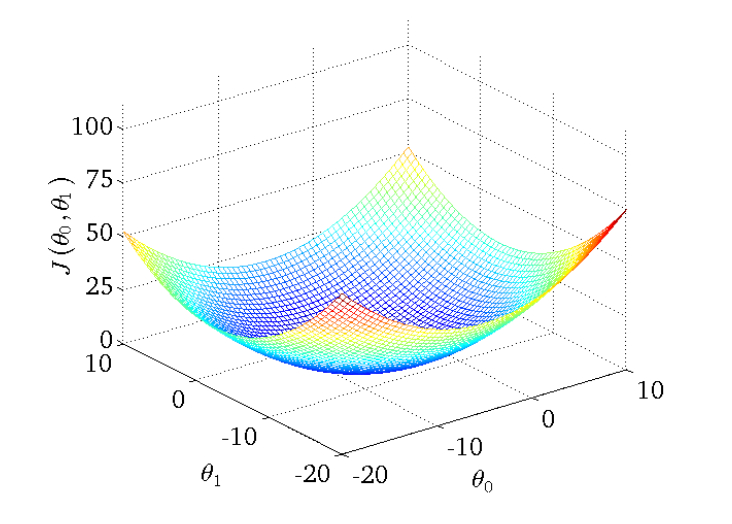
接下来, 我们介绍三种不同的梯度下降算法:

• 批量梯度下降法 (Batch Gradient Descent)
• 随机梯度下降法 (Stochastic Gradient Descent)
• 小批量梯度下降法 (Mini-batch Gradient Descent)

3.1 Batch Gradient Descent

批量梯度下降法 (Batch Gradient Descent, 简称BGD) 是梯度下降法最原始的形式, 它的具体思路是在更新每一参数时都使用所有的样本来进行更新, 其数学形式如下:

Step 1: 对上述的损失函数求偏导

$$\frac{\delta J(\theta)}{\delta\theta_j}=\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x_i)-y_i)x_j$$

Step 2: 由于是最小化风险函数，所以按照每个参数 $\theta$ 的梯度负方向来更新每个 $\theta$

$$\theta_{j_{new}}=\theta_{j_{old}}-\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x_i)-y_i)x_j$$

具体的伪代码形式为

$$\begin{aligned} \mathbf{repeat}&\{ \\ &\theta_{j_{new}}=\theta_{j_{old}}-\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x_i)-y_i)x_j\\ &(for\ every\ j=0,...,n)\\ \} \end{aligned}$$

从上面公式可以注意到, 它得到的是一个全局最优解, 但是每迭代一步, 都要用到训练集所有的数据, 如果样本数目 $m$ 很大, 那么可想而知这种方法的迭代速度! 所以, 这就引入了另外一种方法, 随机梯度下降.

• 优点: 对于严格凸函数而言, 它得到的是一个全局最优解, 且易于理解和并行实现;
• 缺点: 当样本数目很多时, 训练过程会很慢, 因为每一次计算梯度 (也就是更新参数) 的时候都需要所有的样本;

从迭代的次数上来看, BGD迭代的次数相对较少. 其迭代的收敛曲线示意图可以表示如下:

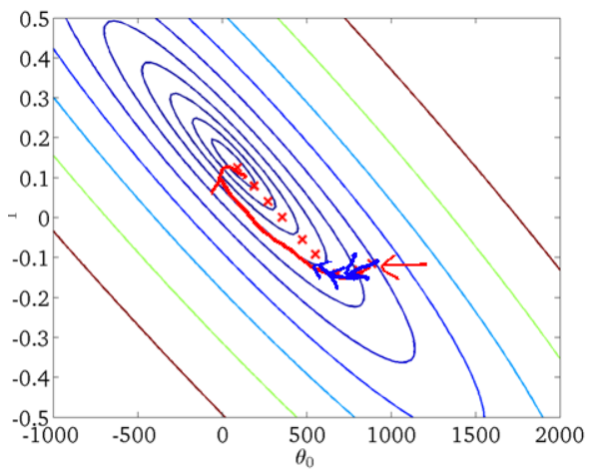
3.2 Stochastic Gradient Descent

由于批量梯度下降法在更新每一个参数时, 都需要所有的训练样本, 所以训练过程会随着样本数量的加大而变得异常的缓慢. 随机梯度下降法 (Stochastic Gradient Descent, 简称SGD) 正是为了解决批量梯度下降法这一弊端而提出的.

它是利用每个样本的损失函数对 $\theta$ 求偏导得到对应的梯度, 来更新 $\theta$:

$$\theta_{j_{new}}=\theta_{j_{old}}-\alpha(h_{\theta}(x_i)-y_i)x_j$$

具体的伪代码形式为

随机梯度下降是通过每个样本来迭代更新一次, 如果样本量很大的情况 (例如几十万), 那么可能只用其中几万条或者几千条的样本, 就已经将theta迭代到最优解了, 对比上面的批量梯度下降, 迭代一次需要用到十几万训练样本, 一次迭代不可能最优, 如果迭代10次的话就需要遍历训练样本10次. 但是, SGD伴随的一个问题是噪音较BGD要多, 使得SGD并不是每次迭代都向着整体最优化方向.

• 优点: 训练速度快;
• 缺点: 准确度下降, 不易于并行实现;

注:

一般在生产中的场景 objective function 都不是单峰的, 自然, BGD 就不一定做到全局最优, 反而是sgd更可能跳出局部最优.

从迭代的次数上来看, SGD迭代的次数较多, 在解空间的搜索过程看起来很盲目. 其迭代的收敛曲线示意图可以表示如下:

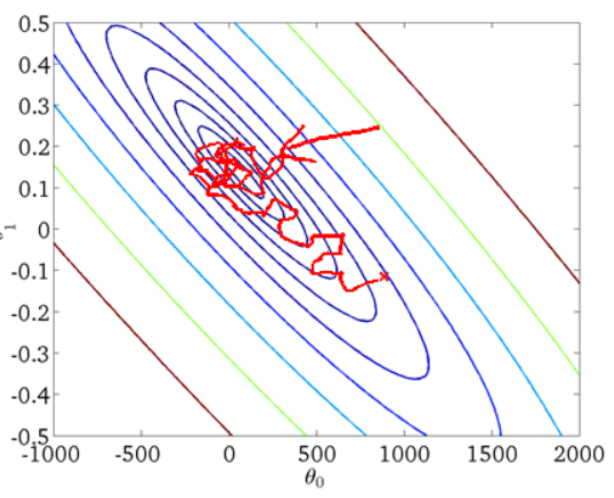
3.3 Mini-batch Gradient Descent

有上述的两种梯度下降法可以看出, 其各自均有优缺点, 那么能不能在两种方法的性能之间取得一个折衷呢? 即, 算法的训练过程比较快, 而且也要保证最终参数训练的准确率, 而这正是小批量梯度下降法 (Mini-batch Gradient Descent, 简称MBGD) 的初衷.

MBGD 在每次更新参数时使用 b 个样本 (b一般为10), 其具体的伪代码形式为:

4. Conclusion

1. 批梯度下降每次更新使用了所有的训练数据, 最小化损失函数, 如果只有一个极小值, 那么批梯度下降是考虑了训练集所有数据, 是朝着最小值迭代运动的, 但是缺点是如果样本值很大的话, 更新速度会很慢.
2. 随机梯度下降在每次更新的时候, 只考虑了一个样本点, 这样会大大加快训练数据, 也恰好是批梯度下降的缺点, 但是有可能由于训练数据的噪声点较多, 那么每一次利用噪声点进行更新的过程中, 就不一定是朝着极小值方向更新, 但是由于更新多轮, 整体方向还是大致朝着极小值方向更新, 又提高了速度.
3. 小批量梯度下降法是为了解决批梯度下降法的训练速度慢, 以及随机梯度下降法的准确性综合而来, 但是这里注意, 不同问题的batch是不一样的.