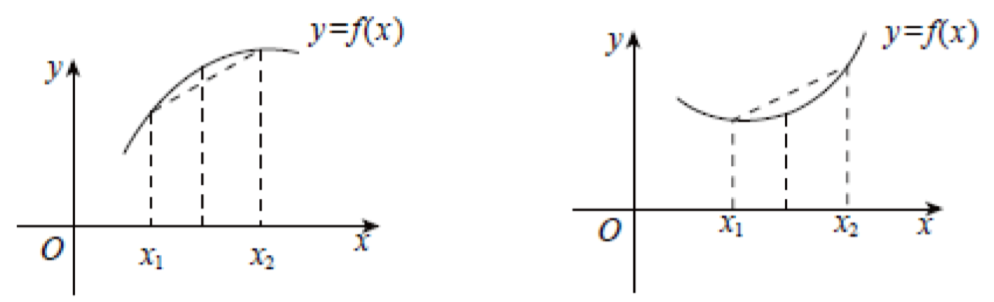机器学习中的 Entropy

1. Information Entropy

信息熵通常用来描述整个随机分布所带来的信息量平均值, 更具统计特性. 信息熵也叫香农熵, 在机器学习中, 由于熵的计算是依据样本数据而来, 故也叫经验熵. 其公式定义如下:

$$H(X)=-E_{x\sim p}[\log P(x)]=-\sum_{i=1}^nP(x_i)\log P(x_i)$$

从公式可以看出, 信息熵 $H(x)$ 是各项自信息的累加值, 由于每一项都是整正数, 故而随机变量取值个数越多, 状态数也就越多, 累加次数就越多, 信息熵就越大, 混乱程度就越大, 纯度越小. 越宽广的分布, 熵就越大. 可以通过数学证明, 当随机变量分布为均匀分布时即状态数最多时, 熵最大. 熵代表了随机分布的混乱程度, 这一特性是所有基于熵的机器学习算法的核心思想.

推广到多维随机变量的联合分布, 其联合信息熵为:

$$H(X,Y)=-\sum_{i=1}^n\sum_{j=1}^mP(x_i,y_i)\log P(x_i,y_i)$$

注意事项:

• 熵只依赖于随机变量的分布, 与随机变量取值无关.
• 定义 $0\log0=0$ (因为可能出现某个取值概率为0的情况).
• 熵越大, 随机变量的不确定性就越大, 分布越混乱, 随机变量状态数越多.

2. Conditional Entropy

条件熵 $H(Y|X)$ 表示在已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性.

$$\begin{equation} \begin{aligned} H(Y|X)=&\sum_{x}P(x)H(Y|X=x) \\ =&\sum_{x}P(x)\sum_{y}P(y|x)\log P(y|x) \\ =&\sum_{x,y}P(x,y)\log P(y|x) \end{aligned} \end{equation}$$

条件熵 $H(Y|X)$ 相当于联合熵 $H(X,Y)$ 减去单独的熵 $H(X)$, 即 $H(Y|X)=H(X,Y)-H(X)$. 举个例子, 比如环境温度是低还是高, 和我穿短袖还是外套这两个事件可以组成联合概率分布 $H(X,Y)$, 因为两个事件加起来的信息量肯定是大于单一事件的信息量的. 假设 $H(X)$ 对应着今天环境温度的信息量, 由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的, 所以在已知今天环境温度的情况下, 我穿什么衣服的信息量或者说不确定性是被减少了. 当已知 $H(X)$这个信息量的时候, $H(X,Y)$ 剩下的信息量就是条件熵: $H(Y|X)=H(X,Y)-H(X)$

3. Relative Entropy

相对熵也被称为 KL 散度.

在我们介绍相对熵之前, 我们先试着思考一个问题, 我们为什么需要相对熵这么一个概念呢?

原因很简单, 因为我们希望测量我们训练出来的模型和实际数据的差别, 相对熵的目的就是为了评估和验证模型学习的效果. 也就是说相对熵是用来衡量两个概率分布的差值的, 我们用这个差值来衡量模型预测结果与真实数据的差距. 明白了这点之后, 我们来看相对熵的定义:

$$D_{KL}(P||Q)=\sum_{i=1}^nP(x_i)\log\frac{P(x_i)}{Q(x_i)}$$

如果把 $\sum_{i=1}^nx_i$ 看成是一个事件的所有结果, 那么所有的 $P(x_i)$ 和 $Q(x_i)$ 就可以看成是两个关于事件 $X$ 的概率分布. 其中: $P(x_i)$ 是样本真实的分布, 而 $Q(x_i)$ 是我们模型产出的分布. KL 散度越小, 表示这两个分布越接近, 说明模型的效果越好.

光看上面的KL 散度公式可能会云里雾里, 不明白为什么能反应P和Q两个分布的相似度. 因为这个公式少了两个限制条件:

$$\sum_{i=1}^nP(x_i)=1,\sum_{i=1}^nQ(x_i)=1$$

我们假设 $x_i$ 只有 0 和 1 两个取值, 也就是一个事件只有发生或者不发生. 我们再假设 $P(x=0)=P(x=1)=0.5$, 我们画一下 $P(x_i)\log(\frac{P(x_i)}{Q(x_i)})$ 的图像:

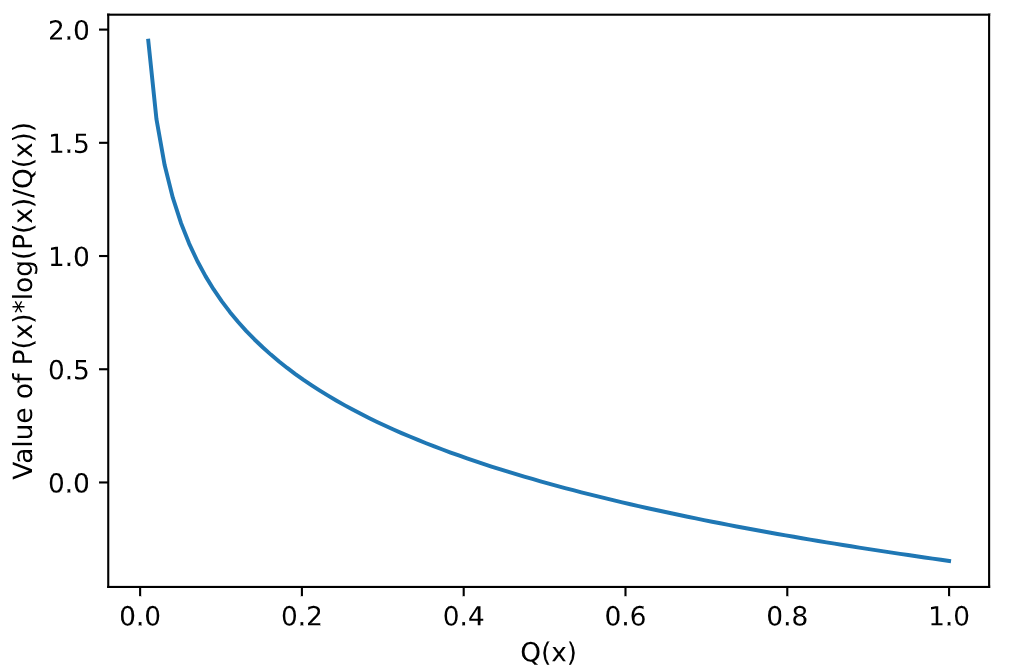
代码如下:

import numpy as np
import matplotlib.pyplot as plt

def kl_function(p_x,q_x):
    return p_x*np.log(p_x/q_x)

p_x = 0.5
q_x = np.linspace(0,1,100)
kl_value = [kl_function(0.5,i) for i in q_x]

plt.plot(q_x,kl_value)
plt.xlabel("Q(x)")
plt.ylabel("Value of P(x)*log(P(x)/Q(x))")
plt.show()

我们可以看到, 函数随着 $Q(x_i)$ 的递增而递减. 但是这只是一个 $x$ 的取值, 别忘了, 我们相对熵计算的是整个分布，那我们加上另一个x的取值会发生什么呢？

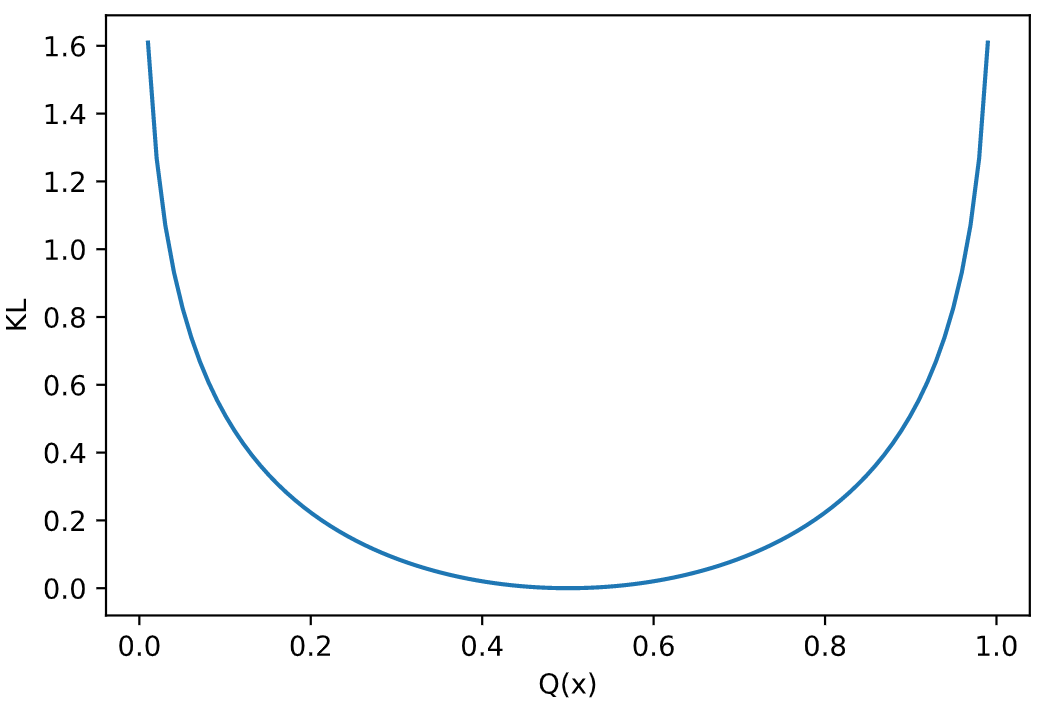
代码如下:

import numpy as np
import matplotlib.pyplot as plt

def kl_function(p_x,q_x):
    return p_x*np.log(p_x/q_x)

p_x = 0.5
q_x = np.linspace(0,1,100)
kl_value = [kl_function(p_x,i)+kl_function(1-p_x,1-i) for i in q_x]

plt.plot(q_x,kl_value)
plt.xlabel("Q(x)")
plt.ylabel("KL")
plt.show()

从函数图像上, 我们很容易看出, 当 $Q(x)=0.5=P(x)$ 的时候, KL散度取最小值, 最小值为0. 我们对相对熵的计算公式做一个变形:

$$D_{KL}(P||Q)=\sum_{i=1}^nP(x_i)\log\frac{P(x_i)}{Q(x_i)}=\sum_{i=1}^nP(x_i)\log P(x_i)-\sum_{i=1}^nP(x_i)\log Q(x_i)$$

这个式子的左边 $\sum_{i=1}^nP(x_i)\log(P(x_i))$ 其实就是 $-H(X)$, 对应于一个确定事件 $X$ 来说, 它的信息熵是确定的, 也就是说 $H(X)$ 是一个常数, $P(x_i)$ 也是常数, $\log$ 函数是一个凹函数, $-log$ 则是凸函数. 因此相对熵的计算公式是一个凸函数.

对于任何凸函数, 有 Jensen 不等式:

$$f(E(x))\le E(f(x))$$

我们简单介绍一下凸凹函数

左为凹函数: 满足 $f(\frac{x_1+x_2}{2})\gt\frac{f(x_1)+f(x_2)}{2}$;

右为凸函数: 满足 $f(\frac{x_1+x_2}{2})\lt\frac{f(x_1)+f(x_2)}{2}$;

我们可以利用 Jensen 不等式来证明: $D_{KL}\ge0$

首先我们对 KL 计算公式进行变形:

$$D_{KL}=\sum_{i=1}^nP(x_i)\log\frac{P(x_i)}{Q(x_i)}=E(\log\frac{P(x_i)}{Q(x_i)})=E[-\log\frac{Q(x_i)}{P(x_i)}]$$

然后我们利用不等式:

$$E[-\log\frac{Q(x_i)}{P(x_i)}]\ge-\log E[\frac{Q(x_i)}{P(x_i)}]=-\log\sum_{i=1}^nP(x_i)\frac{Q(x_i)}{P(x_i)}=-\log\sum_{i=1}^nQ(x_i)=0$$

所以KL散度是一个非负值, 但是为什么当P和Q相等时 (也就是真实模型和预测模型相等时), 能取到最小值呢?

我们令:

$$C(P,P)=-\sum_{i=1}^nP(x_i)\log(P(x_i))$$ $$C(P,Q)=-\sum_{i=1}^nP(x_i)\log(Q(x_i))$$ $$C(P,P)-C(P,Q)=\sum_{i=1}^nP(x_i)\log(\frac{Q(x_i)}{P(x_i)})$$

我们探索 $C(P,P)-C(P,Q)$ 的正负性来判断 $P,Q$ 的关系. 因为 $\log(x)$ 是凹函数, 所以我们根据 Jensen 不等式, 可以得到:

$$a_1\log(x_1)+a_2\log(x_2)+...+a_n\log(x_n)\le\log(a_1x_1+a_2x_2+...+a_nx_n),\quad(\sum_{i=1}^na_i=1)$$

我们将之代入 $\sum_{i=1}^nP(x_i)\log(\frac{Q(x_i)}{P(x_i)})$

$P(x_1)\log(\frac{Q(x_1)}{P(x_1)})+P(x_2)\log(\frac{Q(x_2)}{P(x_2)})+…+P(x_n)\log(\frac{Q(x_n)}{P(x_n)})\le\log(P(x_1)\frac{Q(x_1)}{P(x_1)}+P(x_2)\frac{Q(x_2)}{P(x_2)}+…+P(x_n)\frac{Q(x_n)}{P(x_n)})\le\log(Q(x_1)+Q(x_2)+…+Q(x_n))$

因此 $C(P,P)-C(P,Q)\le0$, 当且仅当 $P=Q$ 时等号成立.

4. Cross Entropy

我们已经知道相对熵 (KL 散度)可以反映两个概率分布的距离情况. 由于P是样本已知的分布, 所以我们可以用KL散度反映Q这个模型产出的结果与P的距离. 距离越近, 往往说明模型的拟合效果越好, 能力越强.

而 Cross Entropy 则只是KL散度去除掉了一个固定的定值的结果.

即 $C(P,Q)=-\sum_{i=1}^nP(x_i)\log(Q(x_i))$. KL散度能够反映P和Q分布的相似程度, 同样交叉熵也可以, 而且交叉熵的计算相比KL散度来说要更为精简一些.

比如我们只考虑二分类的场景, 那么 $C(P,Q)=-P(x=0)\log(Q(x=0))-P(x=1)\log(Q(x=1))$. 我们令 $P(x=0)=y,Q(x=0)=\hat{y}$.

所以上式可以变形为:

$$C(P,Q)=-y\log(\hat{y})-(1-y)\log(1-\hat{y})$$

5. Analysis

当然, 到这里其实还没有结束. 仍然存在一个问题, 可以反映模型与真实分布距离的公式很多, 为什么我们训练模型的时候单单选择了交叉熵呢, 其他的公式不行吗? 为什么呢?

假设我们对模型: $\hat{y}=\sigma(\theta X)$ 选择 MSE(均方误差) 作为损失函数.

此时 $MSE=\frac{(\sigma(\theta X)-y)^2}{2}$

我们对它就关于 $\theta$ 的偏导:

$$\begin{equation} \begin{aligned} MSE'=&(\sigma(\theta X)-y)\cdot\sigma'(\theta X)\cdot X \\ =&0.98*2*\sigma(\theta X)\cdot(1-\sigma(\theta X)) \\ =&0.04 \end{aligned} \end{equation}$$

所以如果我们通过梯度下降来学习的话, $\theta_{next}=\theta-\alpha0.04\theta$.

这个式子看起来很正常, 但是隐藏了一个问题, 就是我们这样计算出来的梯度实在是太小了. 通过梯度下降去训练模型需要消耗大量的时间才能收敛.

如果我们将损失函数换成交叉熵呢?

我们回顾一下交叉熵求梯度之后的公式：

$$\frac{\delta}{\delta\theta}J(\theta)=-(\hat{Y}-Y)\cdot X$$

我们带入上面具体的值, 可以算出来如果使用交叉上来训练, 我们算出来的梯度为1.96, 要比上面算出来的0.04大了太多了. 显然这样训练模型的收敛速度会快很多, 这也是为什么我们训练分类模型采用交叉熵作为损失函数的原因.

究其原因是因为如果我们使用MSE来训练模型的话, 在求梯度的过程当中免不了对sigmoid函数求导. 而正是因为sigmoid的导数值非常小, 才导致了我们梯度下降的速度如此缓慢. 那么为什么sigmoid函数的导数这么小呢? 我们来看下它的图像就知道了:

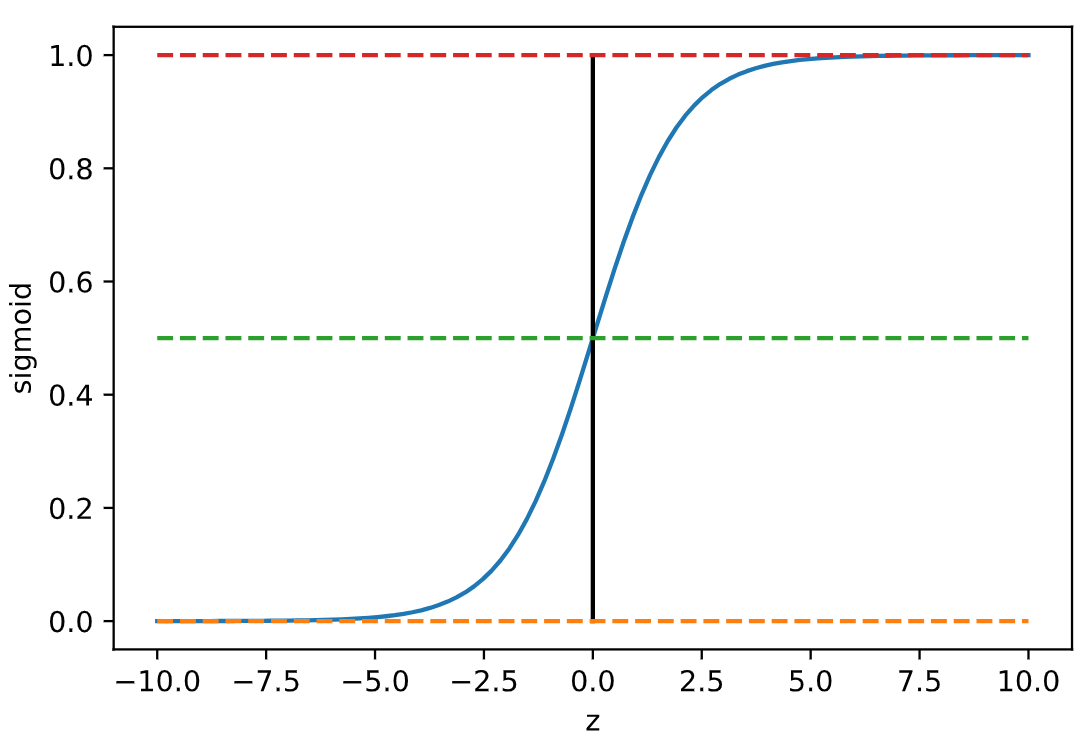
观察一下上面这个图像, 可以发现当x的绝对值大于4的时候, 也就是图像当中距离原点距离大于4的两侧, 函数图像就变得非常平缓. 而导数反应函数图像的切线的斜率, 显然这些区域的斜率都非常小, 而一开始参数稍微设置不合理, 很容易落到这些区间里. 那么通过梯度下降来迭代自然就会变得非常缓慢. 所以无论是机器学习还是深度学习, 我们一般都会少会对sigmoid函数进行梯度下降.