1. Base Algorithm for Decision Tree

  1. Algorithm 1: Memorization Algorithm

    算法的伪代码如下:

    image-20200903205445477

    我们来思考一个问题: Does the memorization algorithm learn?

    答案是 Yes! 因为随着数据集的增大, 我们的准确率会越来越高.

  2. Algorithm 2: Majority Vote Algorithm

    算法伪代码如下:

    image-20200903205526193

    同样我们来看一个问题: What does the majority vote algorithm return on this training data?

    image-20200903203619463

    答案是 +

  3. Algorithm 3: Decision Stump

    核心思想是: Split data based on a single attribute and do majority vote at leaves.

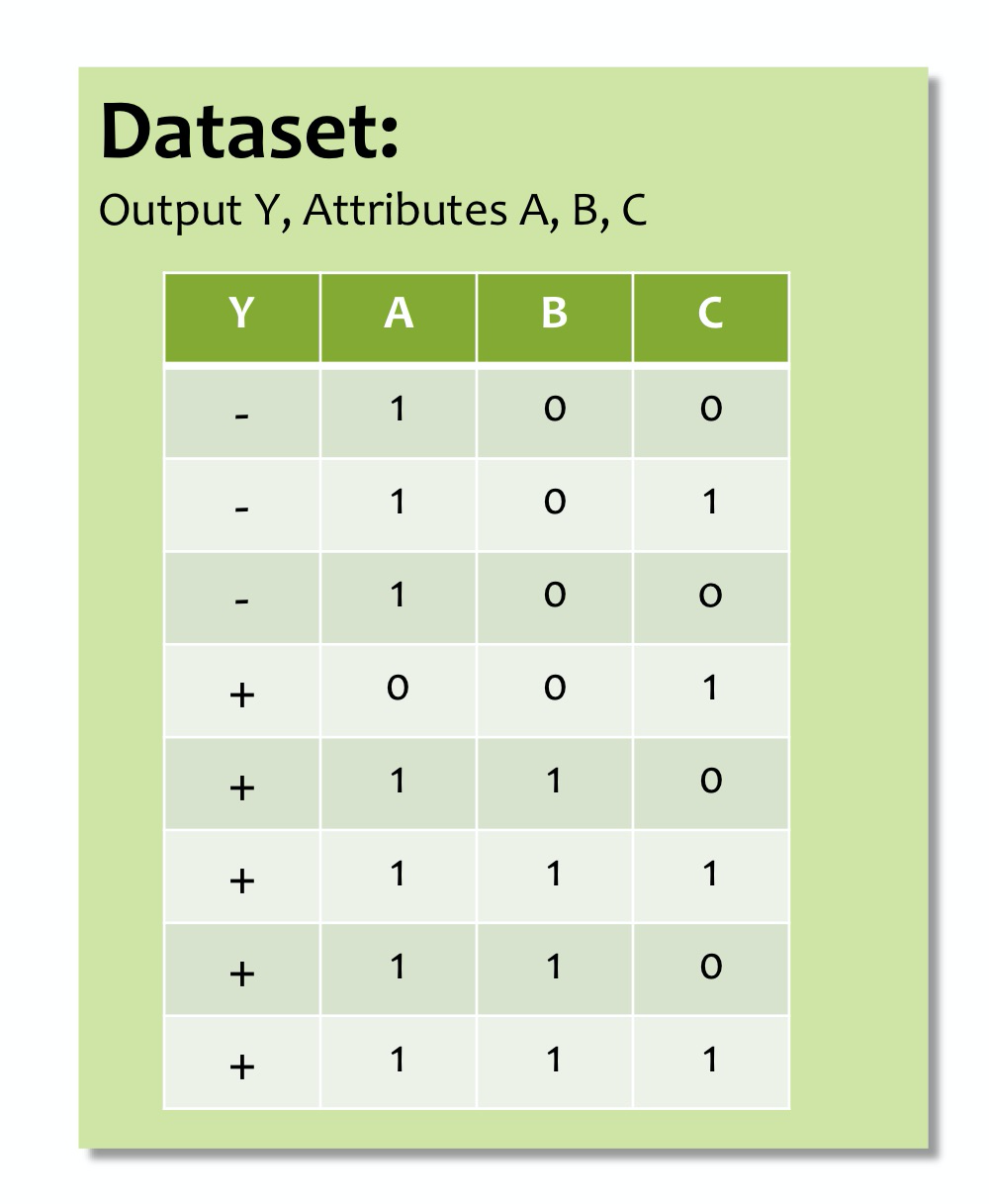
    我们所用到的数据集是:

    image-20200903203619463

    用 Attribute A 的示意图如下: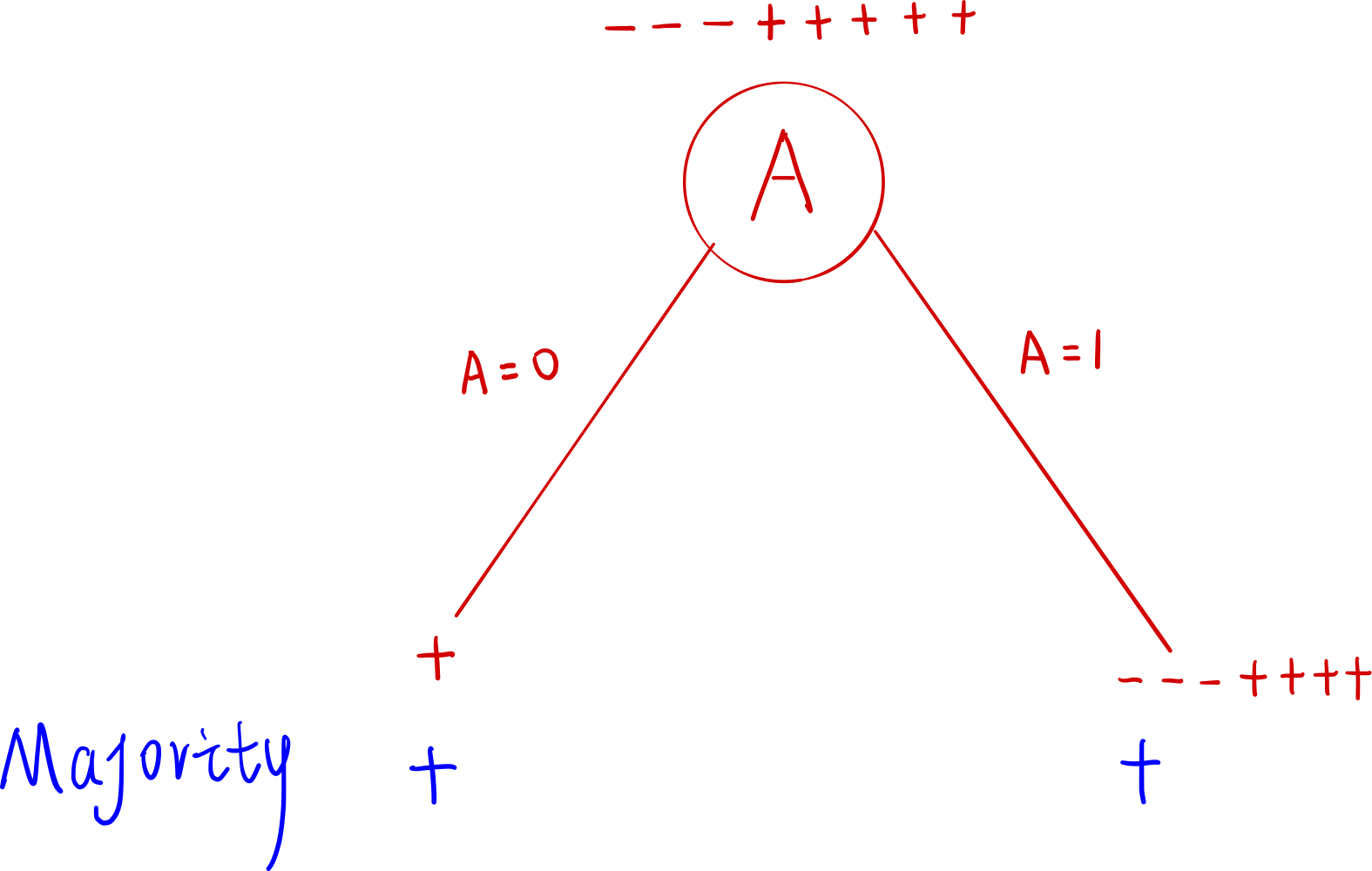

    image-20200903204014704

    算法伪代码如下:

    image-20200903205835284

    如果我们选择 Arribute B, 我们可以得到最低的 Error Rate: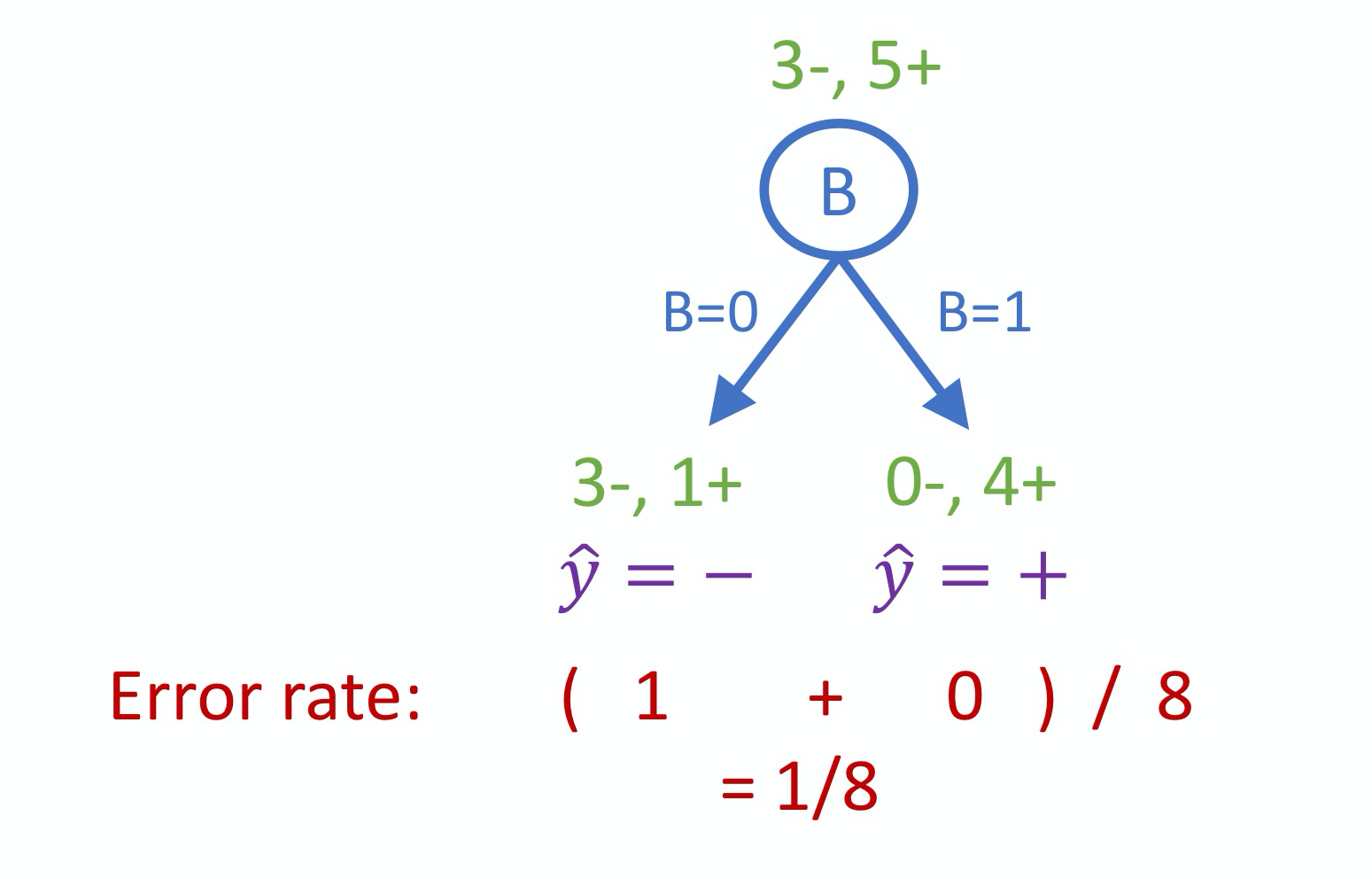

    image-20200903204850653

    相关数学表达:

    image-20200915160058376

2. Decision Tree

我们看一下如何使用一个递归伪代码来建立一个决策树:

image-20200928055729758

显然, 决策树的生成是一个递归过程. 在决策树的基本算法中, 有三种情形会导致递归返回:

  • 当前结点包含的样本全属于同一类别, 无需划分;
  • 当前属性集为空, 或是所有样本在所有属性上取值相同, 无法划分;
  • 当前结点包含的样本集合为空, 不能划分;

在伪代码中我们提到了根据信息增益 (ID3)/信息增益比 (ID4.5)/基尼系数 (CART)来选择最优属性. 而这些数值的计算则是基于我们之前已经介绍过的 Entropy.

在对熵有了基本了解之后, 我们引入 条件熵 和 互信息 的概念. 注: 决策树学习中的信息增益等价于训练集中类与特征的互信息.

image-20200917155140385

在决策树算法中, 我们使用互信息(信息增益)来选择特征. 信息增益越大, 说明该特征对数据集 D 的分类的不确定性消减程度越大. 显然, 对于数据集 D 而言, 不同的特征往往具有不同的信息增益. 信息增益更大的特征具有更强的分类能力.

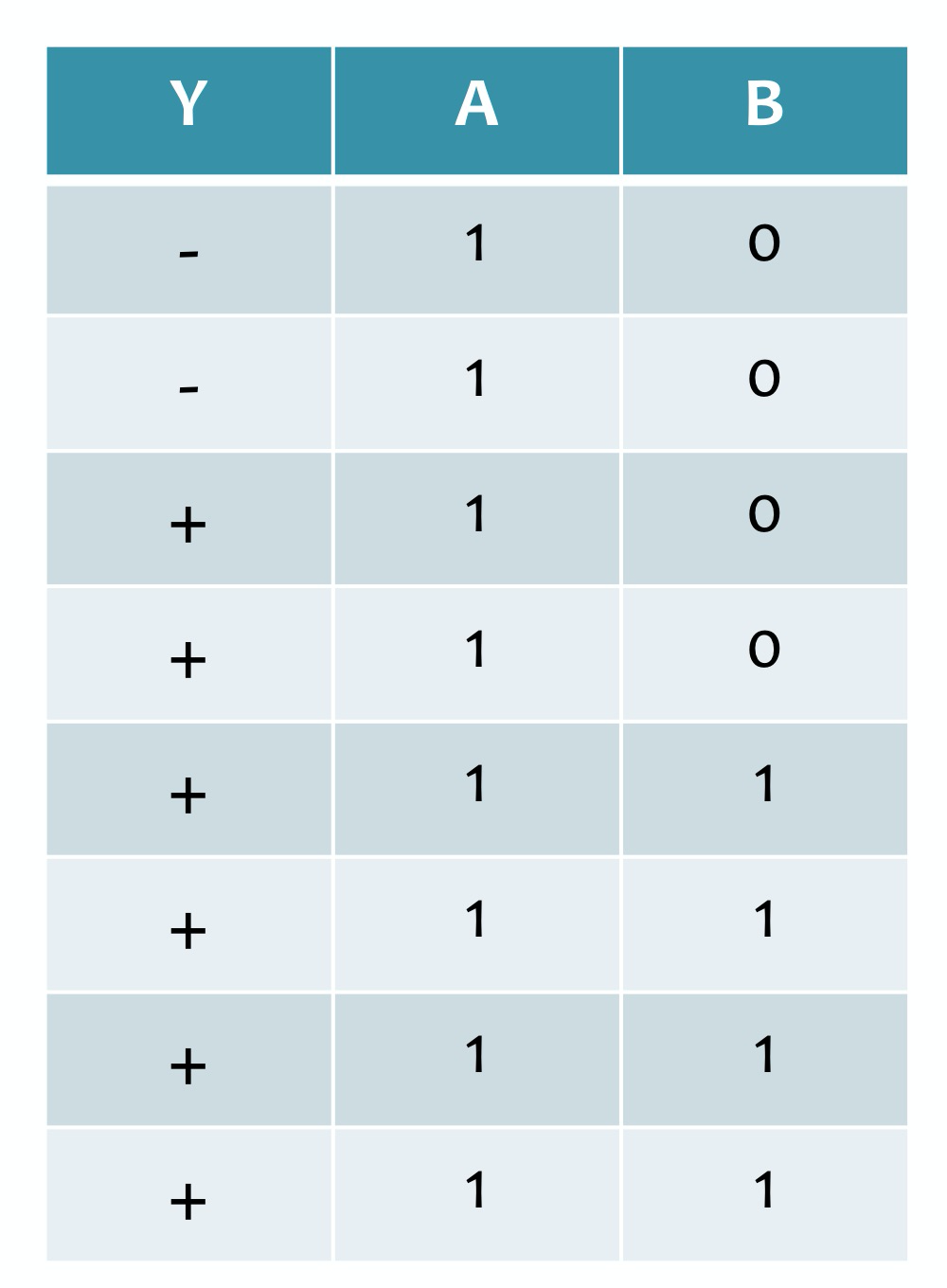
我们看一个例子来熟悉一下信息增益, 数据集如下:

image-20200917160504839

$H(Y)=-\frac{2}{8}\log_2\frac{2}{8}-\frac{6}{8}\log_2\frac{6}{8}=0.811$

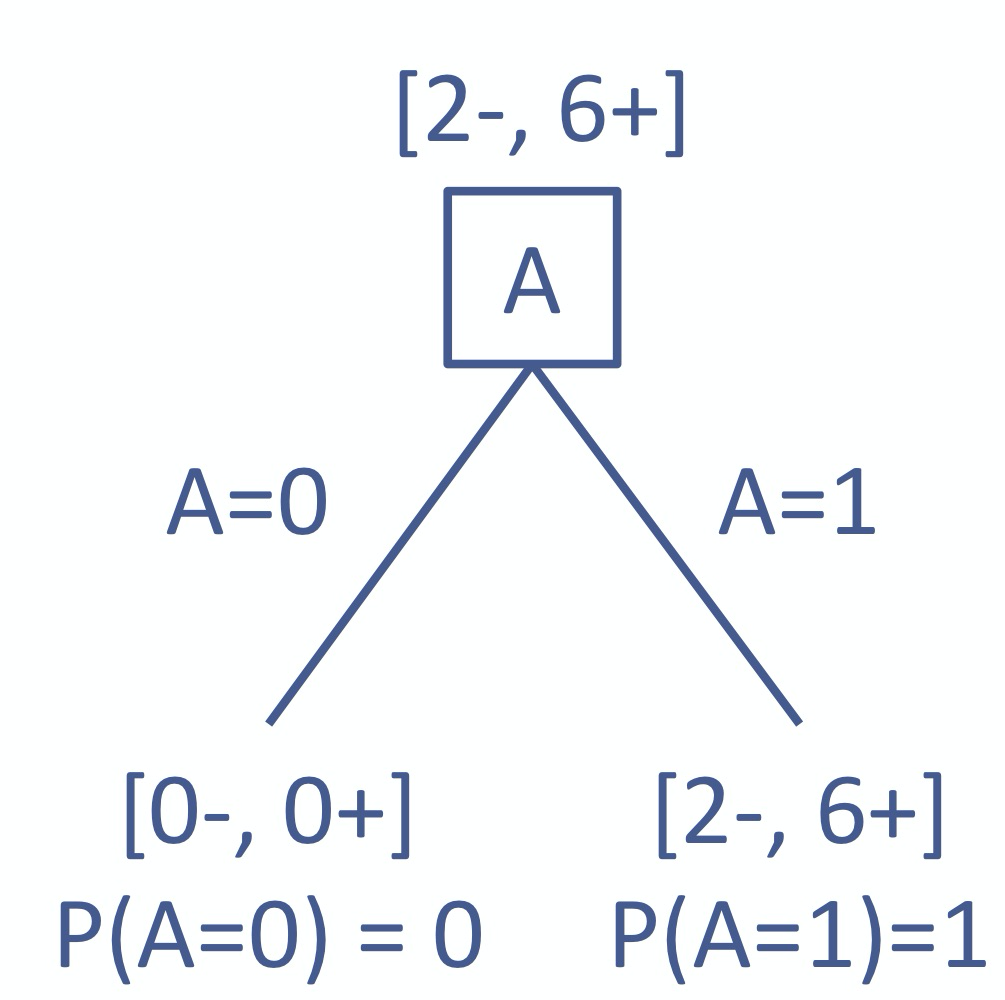
如果使用特征 A:

image-20200917161221017

$H(Y|A=0)=undefined$

$H(Y|A=1)=H(Y)$

$H(Y|A)=P(A=0)H(Y|A=0)+P(A=1)H(Y|A=1)=0+H(Y)=H(Y)$

$I(Y;A)=H(Y)-H(Y|A)=0$

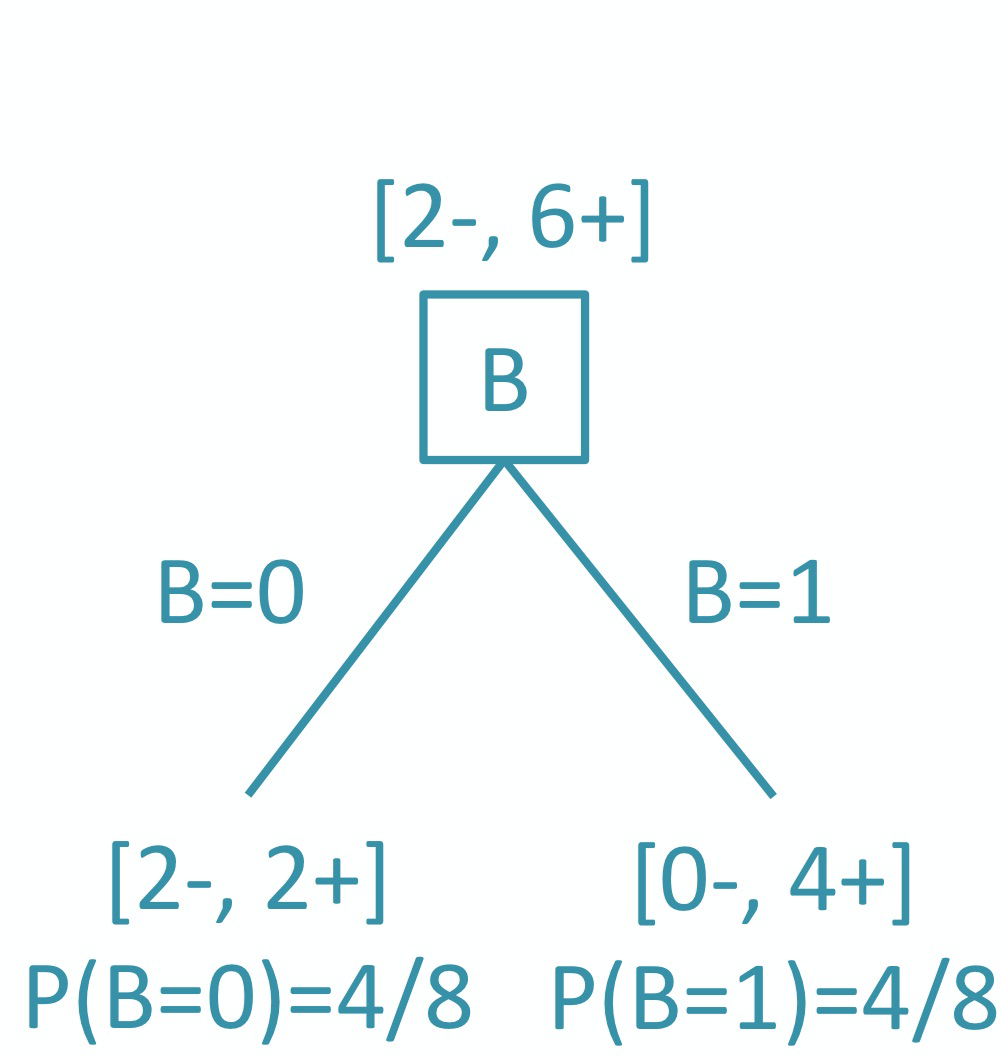
如果使用特征 B:

image-20200917161653256

$H(Y|B=0)=-\frac{2}{4}\log_2\frac{2}{4}-\frac{2}{4}\log_2\frac{2}{4}=1$

$H(Y|B=1)=-0\log_20-1\log_21=0$

$H(Y|B)=P(B=0)H(Y|B=0)+P(B=1)H(Y|B=1)=0.5$

$I(Y;B)=H(Y)-H(Y|B)=0.311$

Since $I(Y;B)>I(Y;A)$, we split on B.

2.1 ID3 and C4.5

我们主要介绍两种决策树经典算法: ID3 和 C4.5.

  1. ID3

    ID3 算法的核心是在决策树各个结点上应用信息增益准则选择特征, 递归的构建决策树. 具体的方法是: 从根结点开始, 对结点计算所有可能的特征的信息增益, 选择信息增益最大的特征作为结点的特征, 由该特征的不同取值建立子节点, 再对子节点递归地调用以上方法, 构建决策树. 直到所有特征的信息增益均很小或没有特征可以选择为止.

    输入: 训练数据集 D, 特征集 A, 阈值 $\varepsilon$

    输出: 决策树 T

    算法步骤:

    1. 若 D 中所有实类属于同一类 $C_k$, 则 T 为单结点树, 并将类 $C_k$ 作为该结点的类标记, 返回 T.
    2. 若 $A=\emptyset$, 则 T 为单结点树, 并将 D 中实例树最大的类 $C_k$ 作为作为该结点的类标记, 返回 T.
    3. 否则, 计算 A 中的各特征对 D 的信息增益, 选择信息增益最大的特征 $A_g$.
    4. 如果 $A_g$ 的信息增益小于阈值 $\varepsilon$, 则设置 T 为单结点树, 并将 D 中实例数最大的类 $C_k$ 作为该结点的类标记, 返回 T.
    5. 否则, 对 $A_g$ 的每一可能值 $a_i$, 依 $A_g=a_i$ 将 D 分割为若干非空子集 $D_i$, 将 $D_i$ 中实例数最大的类作为标记, 构建子结点, 由结点及其子结点构成树 T, 返回 T.
    6. 对第 $i$ 个子结点, 以 $D_i$ 为训练集, 以 $A-\{A_g\}$ 为特征集, 递归地调用步骤 1~5, 得到子树 $T_i$, 返回 $T_i$.

    评价:

    ID3 算法只有树的生成, 所以该算法生成的树容易产生过拟合.

  2. C4.5

    C4.5 算法与 ID3 算法相似, 但有一些改进. C4.5 在生成的过程中, 用信息增益比选择特征.

    输入: 训练数据集 D, 特征集 A, 阈值 $\varepsilon$

    输出: 决策树 T

    算法步骤:

    1. 若 D 中所有实类属于同一类 $C_k$, 则 T 为单结点树, 并将类 $C_k$ 作为该结点的类标记, 返回 T.
    2. 若 $A=\emptyset$, 则 T 为单结点树, 并将 D 中实例树最大的类 $C_k$ 作为作为该结点的类标记, 返回 T.
    3. 否则, 计算 A 中的各特征对 D 的信息增益比, 选择信息增益比最大的特征 $A_g$.
    4. 如果 $A_g$ 的信息增益比小于阈值 $\varepsilon$, 则设置 T 为单结点树, 并将 D 中实例数最大的类 $C_k$ 作为该结点的类标记, 返回 T.
    5. 否则, 对 $A_g$ 的每一可能值 $a_i$, 依 $A_g=a_i$ 将 D 分割为若干非空子集 $D_i$, 将 $D_i$ 中实例数最大的类作为标记, 构建子结点, 由结点及其子结点构成树 T, 返回 T.
    6. 对第 $i$ 个子结点, 以 $D_i$ 为训练集, 以 $A-\{A_g\}$ 为特征集, 递归地调用步骤 1~5, 得到子树 $T_i$, 返回 $T_i$.

    注: 这里我们引入了新概念 信息增益比 (information gain ratio)

    以信息增益作为划分训练数据集的特征, 存在偏向于选择取值数目较多的属性的问题. 使用信息增益比 (information gain ratio) 可以对这一问题进行校正. Information Gain Ratio 的定义如下:

    特征 A 对训练数据集 D 的信息增益比 $g_R(D,A)$ 定义为其信息增益 $g(D,A)$ 与训练数据集 D 关于特征 A 的值熵 $H_A(D)$ 之比, 即

    $g_R(D,A)=\frac{g(D,A)}{H_A(D)}$, 其中 $H_A(D)=-\sum_{i=1}^{n}\frac{|D_i|}{|D|}\log_2\frac{|D_i|}{|D|}$

2.2 CART

CART是“Classification and Regression Trees”的缩写. 从其名字我们就不难理解, CART算法是即可以用于分类, 也可以用于回归的.

2.2.1 Classification

我们针对特征值的类型来分别介绍CART算法是如何进行分类的, 以及和C4.5有什么异同.

  1. 连续特征值

    CART的处理思想与C4.5是相同的, 即将连续特征值离散化. 唯一不同的地方是度量的标准不一样, CART采用基尼指数, 而C4.5采用信息增益比. 下面举个例子说明下:

    特征 $a$ 有连续值 $m$ 个, 从小到大排列:

    $a_1, a_2,a_3,…,a_{m-1},a_m$

    我们对相邻的两个值求平均得到 $m-1$ 个切分点:

    $Split \ 1: \frac{a_1+a_2}{2}$

    $Split\ 2:\frac{a_2+a_3}{2}$

    $…$

    然后我们使用每个切分点把数据集离散划分成两类: $D_1,D_2$, 然后计算每个划分点所对应的基尼系数, 选择值最小的一个作为最终的特征划分.

    基尼系数:

    Gini系数是一种与信息熵累类似的做特征选择的方式, 可以用来衡量数据的不纯度. 计算公式如下:

    其中 $|C_k|$ 表示数据中每个类别也就是 $(Y=y_k)$ 的instances数量. $|D|$ 表示数据中所有instances的数量.

    CART与ID3, C4.5处理离散属性不同的是: 如果当前节点为连续属性, 则该属性后面还可以参与子节点的产生选择过程.

  2. 离散特征值

    CART的处理思想与C4.5稍微所有不同. 如果离散特征值多于两个, 那么C4.5会在节点上根据特征值划分出多叉树. 但是CART则不同, 无论离散特征值有几个, 在节点上都划分成二叉树. CART树是如何进行分类的呢? 我们还是用一个例子来讲解:

    特征 $a$ 有 $m$ 个离散值:

    $a_1,a_2,a_3,…,a_{m-1},a_m$

    分类标准是: 每一次将其中一个特征分为一类, 其它非该特征分为另外一类. 依照这个标准遍历所有的分类情况, 计算每种分类下的基尼指数, 最后选择值最小的一个作为最终的特征划分.

特征值连续和离散有各自的处理方法, 不应该混淆使用. 比如分类0,1,2只代表标签含义, 如果进行加减的运算或者求平均则没有任何意义. 因此, CART分类树会根据特征类型选择不同的划分方法, 并且与C4.5不同是, 它永远只有两个分支.

现在我们给出CART的算法流程:

输入: 训练数据集 $D$, 停止计算的参数条件.

输出: CART 决策树.

算法步骤:

根据训练数据集, 从根节点开始, 递归地对每个结点进行以下操作, 构建二叉决策树.

  1. 如果样本个数小于阈值或者没有特征, 则返回决策子树, 当前节点停止递归.
  2. 计算样本集 $D$ 的基尼系数, 如果基尼系数小于阈值, 则返回决策子树, 当前节点停止递归.
  3. 识别各个特征类型, 是离散值还是连续值? 对每种类型使用相应的处理方法并计算每个切分下的基尼系数.
  4. 在计算出来的各个特征的各个特征值对数据集 $D$ 的基尼系数中, 选择基尼系数最小的特征 $A$ 和对应的特征值 $a$. 根据这个最优特征和最优特征值, 把数据集划分成两部分 $D_1$ 和 $D_2$, 同时建立当前节点的左右节点, 左节点的数据集 $D$ 为 $D_1$, 右节点的数据集 $D$ 为 $D_2$.
  5. 对左右的子节点递归的调用1-4步, 生成决策树.

算法停止计算的条件是: 如步骤1,2所示, 结点中的样本个数小于预定的阈值. 或样本集的Gini系数小于预定阈值 (样本基本属于同一类), 或者没有更多的特征.

2.2.2 Regression

与分类树不同, 回归树的预测变量是连续值, 比如预测一个人的年龄, 又或者预测季度的销售额等等. 另外, 回归树在选择特征的度量标准和决策树建立后预测的方式上也存在不同.

  1. 预测方式

    一个回归树对应着输入特征空间的一个划分, 以及在划分单元上的输出值. 先假设数据集已被划分为 $R_1,R_2,…,R_m$ 共 $m$ 个子集, 回归树要求每个划分 $R_m$ 中都对应一个固定的输出值 $c_m$.

    这个 $c_m$ 值其实就是每个子集中所有样本的目标变量 $y$ 的平均值, 并以此 $c_m$ 作为该子集的预测值. 所有分支节点都是如此, 叶子节点也不例外. 因此, 可以知道回归树的预测方式是: 将叶子节点中样本的y均值作为回归的预测值. 而分类树的预测方式则是: 叶子节点中概率最大的类别作为当前节点的预测类别.

  2. 选择特征的度量标准

    CART回归树对于特征类型的处理与分类树一样, 连续值与离散值分开对待, 并只能生成二叉树. 但是CART回归树对于选择特征的度量标准则完全不同.

    分类树的特征选择标准使用基尼指数, 而回归树则使用RSS残差平方和. 了解线性回归的朋友知道, 损失函数是以最小化离差平方和的形式给出的. 回归树使用的度量标准也是一样的, 通过最小化残差平方和作为判断标准，公式如下:

    我们首先遍历变量 $j$, 对固定的切分变量 $j$ 扫描切分点 $s$, 选择使上式达到最小的对 $(j,s)$.

    然后我们用选定的对 $(j,s)$ 划分区域并决定相应的输出值:

    我们继续对两个子区域调用上述两个步骤, 直至满足停止条件.

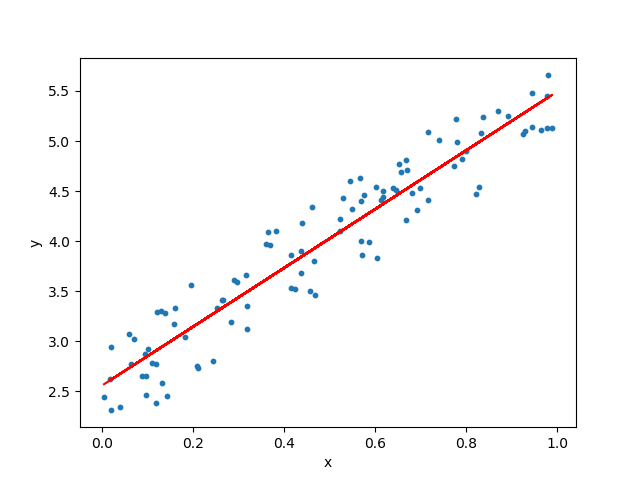
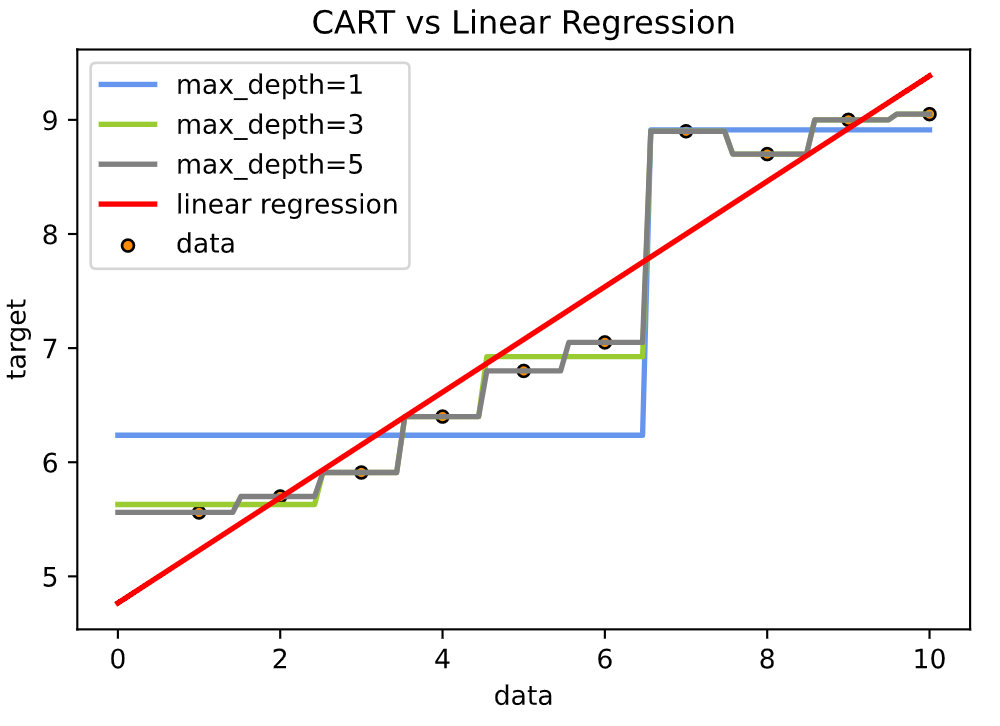
我们来看一个回归树的例子, 训练数据见下表, 目标是得到一棵最小二乘回归树.

x 1 2 3 4 5 6 7 8 9 10
y 5.56 5.7 5.91 6.4 6.8 7.05 8.9 8.7 9 9.05

我们第一步需要选择最优切分变量 $j$ 和最优切分点 $s$. 在本数据集中, 只有一个变量, 因此最优切分变量自然是 $x$. 接下来我们考虑9个切分点[ 1.5 , 2.5 , 3.5 , 4.5 , 5.5 , 6.5 , 7.5 , 8.5 , 9.5 ]. 例如, 如果我们取 $s=1.5$, 此时 $R_1=\{1\}$, $R_2=\{2,3,4,5,6,7,8,9,10\}$. 这两个区域的输出值分别为: $c_1=5.56$, $c_2=7.5$. 因此我们能得到下表:

s 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5
$c_1$ 5.56 5.63 5.72 5.89 6.07 6.24 6.62 6.88 7.11
$c_2$ 7.5 7.73 7.99 8.25 8.54 8.91 8.92 9.03 9.05

然后我们计算不同切分点下的残差和, 即 $\sum_{x_i\in R_1(j,s)}(y_i-c_1)^2+\sum_{x_2\in R_2(j,s)}(y_i-c_2)^2$, 我们能得到下表:

s 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5
rss 15.72 12.08 8.37 5.78 3.91 1.93 8.00 11.74 15.74

显然当 $s=6.5$ 时, 残差和取得最小. 因此第一个划分对为 $(j=x,s=6.5)$.

接下来就是递归生回归树, 过程不在此赘述, 直接看代码.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Declare Package
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model
import matplotlib.pyplot as plt

# Dataset
x = np.arange(1,11).reshape(-1,1)
y = np.array([5.56,5.7,5.91,6.4,6.8,7.05,8.9,8.7,9,9.05]).ravel()

# Fit Model
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = DecisionTreeRegressor(max_depth=5)
model4 = linear_model.LinearRegression()

model1.fit(x,y)
model2.fit(x,y)
model3.fit(x,y)
model4.fit(x,y)

# Predict
x_test = np.linspace(0,10,100).reshape(-1,1)
y_1 = model1.predict(x_test)
y_2 = model2.predict(x_test)
y_3 = model3.predict(x_test)
y_4 = model4.predict(x_test)

# Plot the results
plt.figure()
plt.scatter(x,y,s=20,edgecolor="black",c="darkorange",label="data")
plt.plot(x_test,y_1,color="cornflowerblue",label="max_depth=1",linewidth=2)
plt.plot(x_test,y_2,color="yellowgreen",label="max_depth=3",linewidth=2)
plt.plot(x_test,y_3,color="grey",label="max_depth=5",linewidth=2)
plt.plot(x_test,y_4,color="red",label="linear regression",linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("CART vs Linear Regression")
plt.legend()
plt.show()

image-20201217232054452

3. Pros and Cons

决策树的优势:

  • 便于理解和解释。树的结构可以可视化出来。
  • 训练需要的数据少。其他机器学习模型通常需要数据规范化，比如构建虚拟变量和移除缺失值,不过请注意，这种模型不支持缺失值。
  • 由于训练决策树的数据点的数量导致了决策树的使用开销呈指数分布(训练树模型的时间复杂度是参与训练数据点的对数值)。
  • 能够处理数值型数据和分类数据。其他的技术通常只能用来专门分析某一种变量类型的数据集。详情请参阅算法。
  • 能够处理多路输出的问题。
  • 使用白盒模型。如果某种给定的情况在该模型中是可以观察的，那么就可以轻易的通过布尔逻辑来解释这种情况。相比之下，在黑盒模型中的结果就是很难说明清楚地。
  • 可以通过数值统计测试来验证该模型。这对事解释验证该模型的可靠性成为可能。
  • 即使该模型假设的结果与真实模型所提供的数据有些违反，其表现依旧良好。

决策树的缺点包括:

  • 决策树模型容易产生一个过于复杂的模型,这样的模型对数据的泛化性能会很差。这就是所谓的过拟合.一些策略像剪枝、设置叶节点所需的最小样本数或设置数的最大深度是避免出现 该问题最为有效地方法。
  • 决策树可能是不稳定的，因为数据中的微小变化可能会导致完全不同的树生成。这个问题可以通过决策树的集成来得到缓解
  • 在多方面性能最优和简单化概念的要求下，学习一棵最优决策树通常是一个NP难问题。因此，实际的决策树学习算法是基于启发式算法，例如在每个节点进 行局部最优决策的贪心算法。这样的算法不能保证返回全局最优决策树。这个问题可以通过集成学习来训练多棵决策树来缓解,这多棵决策树一般通过对特征和样本有放回的随机采样来生成。
  • 有些概念很难被决策树学习到,因为决策树很难清楚的表述这些概念。例如XOR，奇偶或者复用器的问题。
  • 如果某些类在问题中占主导地位会使得创建的决策树有偏差。因此，我们建议在拟合前先对数据集进行平衡。

4. Implementation

项目一地址: https://github.com/alvisdeng/Decision-Tree-ID3

说实话, 这份代码我写的不是很满意, 主要是因为那个时候刚开始接触… 后续有时间再做优化吧… 主要是写的太啰嗦了.

项目二: 使用Sklearn的CART分类树

数据使用项目一的Education Dataset

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import pandas as pd
import numpy as np
from sklearn import tree
import graphviz

train_file = "data/education_train.tsv"
test_file = "data/education_test.tsv"

# Preprocessing
train_data = pd.read_csv(filepath_or_buffer=train_file,
                         sep="\t",
                         encoding="utf8",
                         converters={
                             "M1":lambda x:np.where(x=="A",1,0),
                             "M2":lambda x:np.where(x=="A",1,0),
                             "M3":lambda x:np.where(x=="A",1,0),
                             "M4":lambda x:np.where(x=="A",1,0),
                             "M5":lambda x:np.where(x=="A",1,0),
                             "P1":lambda x:np.where(x=="A",1,0),
                             "P2":lambda x:np.where(x=="A",1,0),
                             "P3":lambda x:np.where(x=="A",1,0),
                             "P4":lambda x:np.where(x=="A",1,0),
                             "F":lambda x:np.where(x=="A",1,0)
                         })

test_data = pd.read_csv(filepath_or_buffer=test_file,
                         sep="\t",
                         encoding="utf8",
                         converters={
                             "M1":lambda x:np.where(x=="A",1,0),
                             "M2":lambda x:np.where(x=="A",1,0),
                             "M3":lambda x:np.where(x=="A",1,0),
                             "M4":lambda x:np.where(x=="A",1,0),
                             "M5":lambda x:np.where(x=="A",1,0),
                             "P1":lambda x:np.where(x=="A",1,0),
                             "P2":lambda x:np.where(x=="A",1,0),
                             "P3":lambda x:np.where(x=="A",1,0),
                             "P4":lambda x:np.where(x=="A",1,0),
                             "F":lambda x:np.where(x=="A",1,0)
                         })
                         
train_data['Target'] = train_data['grade'].apply(lambda x:np.where(x=="A",1,0))
test_data['Target'] = test_data['grade'].apply(lambda x:np.where(x=="A",1,0))

# Extract Data
features = list(train_data.columns[:-2])
class_names = sorted(train_data["grade"].unique(),reverse=True)
train_X = train_data[features]
train_Y = train_data["Target"]

test_X = test_data[features]
test_Y = test_data["Target"]

# Train Model
dt = tree.DecisionTreeClassifier(criterion="gini",splitter="best",max_depth=3,random_state=99)
dt.fit(train_X,train_Y)

# Prediction
prediction = dt.predict(test_X)

# Evaluation
score = accuracy_score(y_pred=prediction,y_true=test_Y)
print(score)

# Visualize DT
dot_data = tree.export_graphviz(dt,out_file=None,feature_names=features,class_names=class_names,filled=True,rounded=True,special_characters=True)
graph = graphviz.Source(dot_data)
graph.render("Education")