1. Basic Knowledge

通常我们把分类错误的样本数占总数的比例称为 “错误率” (error rate), 即如果在 m 个样本中有 a 个样本分类错误, 则错误率 $E=a/m$. 相应的, $1-a/m$ 称为 “精度” (accuracy).

训练误差 (training error) 或 经验误差 (empirical error): 学习器在训练集上的误差.

泛化误差 (generalizaiton error): 学习器在测试集上的误差.

很显然, 我们希望得到泛化误差较小的学习器. 但是我们提前是不知道新样本是什么样的, 实际我们能做的就是努力使经验误差最小化. 但是在训练集上做的好, 不代表其能在测试集上做的好. 这就引出了两种现象:

  • 过拟合 (Overfitting)

    学习器把训练样本学得”太好”, 已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质, 这样就会导致泛化性能下降.

  • 欠拟合 (Underfitting)

    对训练样本的一般性质尚未学好

欠拟合比较好解决, 麻烦的是过拟合. 实际工作中大多数时候都是在处理过拟合. 各类学习算法都必然带有一些针对过拟合的措施, 然而我们必须认识到, 过拟合是无法避免的, 我们所能做的只是”缓解”.

2. Model Evaluation

通常, 我们可以通过测试集 (testing set) 来测试学习器对新样本的判别能力, 然后以测试集上的测试误差 (testing error) 作为泛化误差的近似. 通常我们假设测试样本也是从样本真实分布中独立同分布采样而得. 但需注意的是, 测试集应该尽可能与训练集互斥, 即测试样本尽量不在训练集中出现且未在训练过程中使用过.

可是, 我们只有一个包含 m 个样例的数据集 $D$, 既要训练, 又要测试, 怎么才能做到呢? 答案是: 通过对 $D$ 进行适当的处理, 从中产生出训练集 $S$ 和测试集 $T$. 我们在这里介绍几种常见的做法:

  • 留出法(hold-out): 数据量大
  • 交叉验证法(cross validatation): 数据量大
  • 自助法(bootstrapping): 数据量小

2.1 Hold-Out

留出法直接将数据集 $D$ 划分为两个互斥的集合, 其中一个集合作为训练集 $S$, 另外一个作为测试集 $T$, 即 $D=S\cup T,S\cap T=\emptyset$. 我们在 S 上训练出模型之后, 用 $T$ 来评估器测试误差, 作为对泛化误差的估计.

对于留出法, 我们需要注意的是要尽量保证 $S$ 和 $T$ 的数据分布的一致性, 避免因数据划分过程中引入额外的偏差而对最终结果产生影响.

举个例子, 在分类任务中, 我们至少要保证样本的类别比例相似.

如果从采样 (sampling) 的角度来看待数据的划分过程, 则保留类别比例的采样方式通常称为分层采样 (stratified sampling). 我们现在通过对 $D$ 进行分层采样获得 70% 样本的训练集 $S$ 和含 30% 样本的测试集 $T$. 若 $D$ 包含 500 个正例, 500 个反例, 则我们的训练集 $S$ 应该包含 350 个正例和 350 个反例, 而测试集 $T$ 应该包含 150 个正例和 150 个反例.

若 $S,T$ 中的样本类别比例差别很大, 则误差估计将由于 $S,T$ 数据分布的差异而产生一定的偏差.

在上面的例子中, 还有一个问题. 在构建 $S$ 或者 $T$ 的时候, 我们可以对 $D$ 进行排序, 然后将前 350 个正例或最后 350 个正例放到训练集中. 这些不同的划分将使我们得到不同的 $S$ 和 $T$, 进而模型评估的结果也会有差别, 因此单次留出法的结果往往不是很可靠.

所以再实际操作留出法的时候, 我们可能需要进行 100 次随机划分, 每次产生一组 $S,T$ 用于评估, 而最后的结果是这 100 次评估的平均值. 通过这样做, 我们同样可以得到估计结果的标准差.

Another problem

尽管我们做了上面的范例操作, 但是同样还存在一个问题. 我们在划分训练集和测试集的时候, 需要指定比例. 试想: 若我们令训练集 $S$ 包含过多的样本, 那么我们训练得到模型可能更接近用 $D$ 训练出来的模型, 但由于 $T$ 比较小, 评估结果可能不够稳定和准确. 同理, 训练集比较小也会出现相应的问题. 但对于这个问题, 我们并没有完美的解决方案, 常见的做法是将大约 2/3 ~ 4/5 的样本用于训练, 剩余样本用于测试.

2.2 Cross Validation

交叉验证法先将数据集 $D$ 划分为 k 个大小相似的互斥子集, 即 $D=D_1\cup D_2\cup …\cup D_k,D_i\cap D_j=\emptyset(i\ne j).$ 其中每个子集 $D_i$ 都尽可能保持数据分布的一致性, 即从 $D$ 中通过分层采样得到

然后, 我们每次使用 $k-1$ 个子集的并集作为训练集, 余下的那个子集作为测试集. 这样我们就能获得 $k$ 组训练/测试集, 从而可以进行 $k$ 次训练和测试, 最终返回的是这 $k$ 个测试结果的均值. $k$ 最常用的取值是 10, 此时称为 10 折交叉验证; 其他常用的 k 值有 5, 20 等.

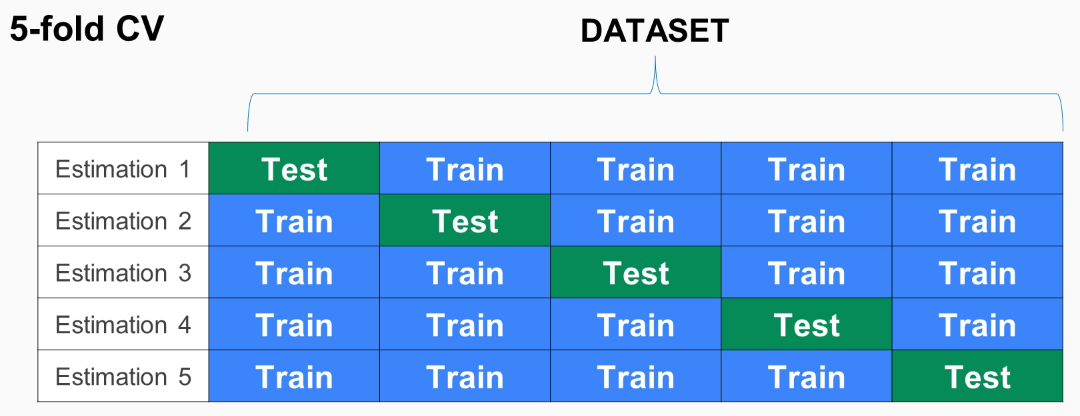
K-fold cross-validation - Mastering Predictive Analytics with scikit-learn and TensorFlow

与留出法相似, 将数据集 $D$ 划分为 k 个子集同样存在多种划分方式. 为减小因样本划分不同而引入的差别, $k$ 折交叉验证通常要随机使用不同的划分重复 $p$ 次, 最终的评估结果是这 $p$ 次 $k$ 折交叉验证结果的均值, 例如常见的有 “10 次 10 折交叉验证”.

假设数据集 $D$ 中包含 $m$ 个样本, 若令 $k=m$, 则得到交叉验证法的一个特例: 留一法 (Leave-One-Out, 简称 LOO). 显然, 留一法不受随机样本划分方式的影响, 因为 $m$ 个样本只有唯一的方式划分 $m$ 个子集 — 每个子集包含一个样本. 留一法使用的训练集与初始数据集相比只少了一个样本, 这就使得在绝大数情况下, 留一法中被实际评估的模型与期望评估的用 $D$ 训练出的模型很相似. 因此, 留一法的评估结果往往被认为比较准确. 然而, 留一法也有其缺陷: 在数据集比较大时, 训练 $m$ 个模型的计算开销可能是难以忍受的 (例如数据集包含 1 百万个样本, 则需训练 1 百万个模型), 而这还是在未考虑算法调参的情况下.

2.3 Bootstrapping

我们现在已经大概了解了留一法和交叉验证法的优缺点. 那么是否存在一个方法: 可以减少训练样本规模不同造成的影响, 同时还能比较高效地进行实验估计呢?

自助法 (boostrapping) 是一个比较好的解决方案, 它直接以自助采样法 (bootstrap sampling) 为基础. 给定包含 $m$ 个样本的数据集 $D$, 我们对它进行采样数据集 $D’$: 每次随机从 $D$ 中挑选一个样本, 将其拷贝放入 $D’$, 然后再将该样本放回初始数据集 $D$ 中, 使得该样本在下次采样时仍有可能被采到; 这个过程重复执行 $m$ 次后, 我们就得到了包含 $m$ 个样本的数据集 $D’$, 这就是自助采样的结果. 显然, $D$ 中的一部分样本会在 $D’$ 中多次出现, 而另外一部分样本不出现. 我们可以做一个简单的估计, 样本在 $m$ 次采样中始终不被采到的概率是 $(1-\frac{1}{m})^m$, 取极限得到:

通过自助采样, 初始数据集 $D$ 中约有 36.8% 的样本未出现在采样数据集 $D’$ 中. 于是我们可以将 $D’$ 用作训练集, $D\backslash D’$ 用作测试集.

3. Parameter Tuning

参数配置不同, 我们得到的模型的性能往往有显著的差别.

机器学习中很多算法的参数选择往往是在实数范围内取值, 因此, 对每种参数配置都训练出来模型是不可行的. 比较常见的做法, 是对每个参数选定一个范围和变化步长. 但是这样的参数选定往往得到的结果都不是最佳值, 但是这是在计算开销和性能估计之间进行折中的结果.

但其实, 在这种折中之后, 调参依然很困难. 举个例子, 我们的算法有 3 个参数, 每个参数仅考虑 5 个候选值, 这样对每一组训练/测试集就有 $5^3=125$ 个模型需要考察. 然而很多机器学习算法往往有很多参数需要设定, 这就意味着我们的调参工程量极大.

需要注意的是, 我们通常把学得模型在实际使用中遇到的数据成为测试数据, 为了加以区分, 模型评估与选择中用于评估测试的数据集常称为 验证集 (validation set).

在研究不同算法的泛化性能时, 我们用测试集上的判别效果来估计模型在实际使用时的泛化能力.

而把训练数据另外划分为训练集和验证集, 基于验证集上的性能来进行模型选择和调参.

4. Performance Measure

性能度量反映了任务需求, 在对比不同的模型的能力时, 使用不同的性能度量往往会导致不同的评判结果; 这意味着模型的好坏是相对的, 什么样的模型是好的, 不仅取决于算法和数据, 还取决于任务需求.

4.1 Error Rate and Accuracy

本节开头, 在介绍基础知识的时候, 我们就谈到了错误率和精度. 这是分类任务中最常用的两种性能度量, 既适用于二分类任务, 也适用于多分类任务.

错误率是分类错误的样本数占样本总数的比例, 精度则是分类正确的样本数占样本总数的比例.

4.2 Precision, Recall and F1

错误率和精度虽然常用, 但并不能满足所有任务需求. 以西瓜问题为例, 假定瓜农拉来了一车西瓜, 我们用训练好的模型对这些西瓜进行判别, 显然, 错误率衡量了有多少比例的瓜被判别错误. 但是若我们关心的是挑出来的西瓜中有多少比例是好瓜或者所有好瓜中有多少比例被挑了出来. 那么错误率就不合适了, 这个时候我们就需要使用其他的性能度量.

所以, 我们在这里就引入两个新的度量:

  • 查准率 (precision)
  • 查全率 (recall)

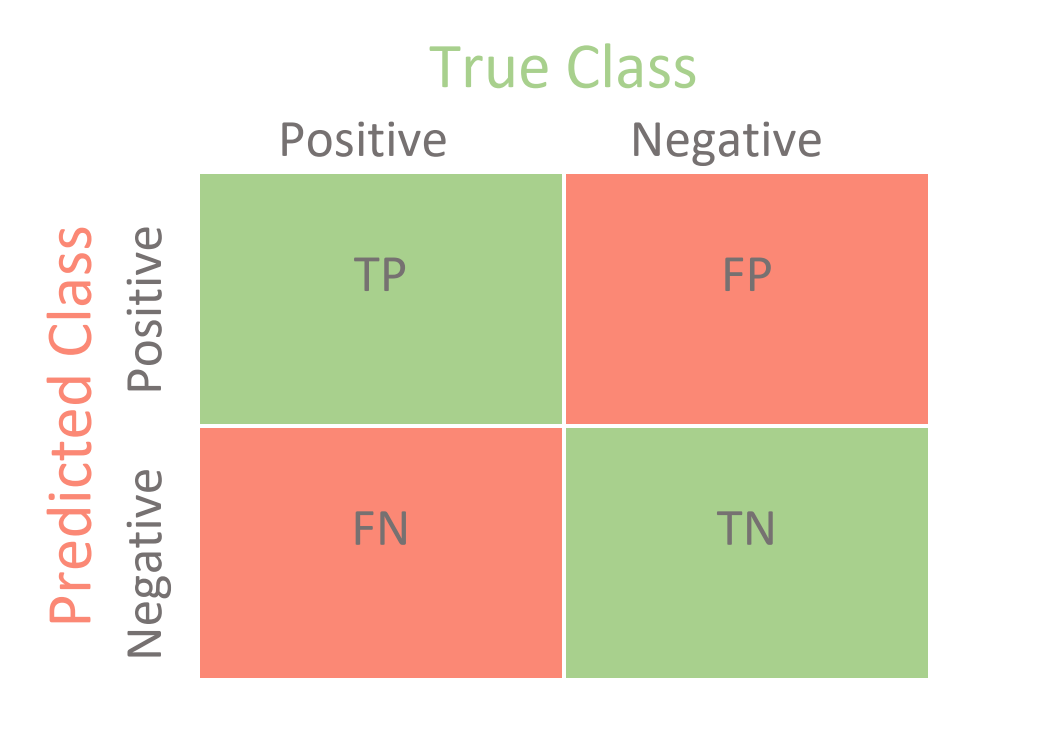
对于二分类问题, 可将样例根据其真实类别与学习器预测类别的组合划分为真正例 (true positive), 假正例 (false positive), 真反例 (true negative), 假反例 (false negative) 四种情形. 令 TP, FP, TN, FN 分别表示其对应的样例数, 则显然有 TP+FP+TN+FN=样例总数. 分类结果的 混淆矩阵 (confusion matrix) 如下图所示.

Confusion Matrix for Your Multi-Class Machine Learning Model | by Joydwip Mohajon | Towards Data Science

查准率 $Precision$ 和查全率 $Recall$ 分别定义为:

查准率和查全率是一对矛盾的度量. 一般来说, 查准率高时, 查全率往往偏低. 例如, 若希望将好瓜尽可能多地选出来, 则可通过增加选瓜的数量来实现, 如果将所有西瓜都选上, 那么所有的好瓜也必然都被选上了, 但这样查准率就会降低. 若希望选出的好瓜中好瓜比例尽可能高, 则可只挑选最有把握的瓜, 但这样就难免会漏掉不少好瓜, 使得查全率较低. 通常只有在一些简单任务中, 才可能使查全率和查准率都很高.

img

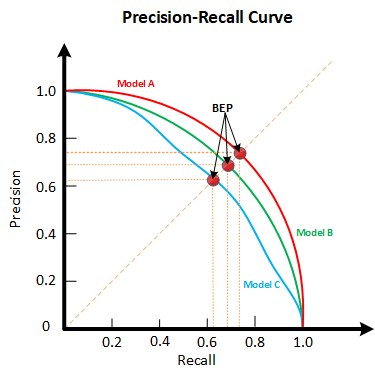
$P-R$ 图直观地显示出学习器在样本总体上的查全率, 查准率. 在进行比较时, 若一个学习器的 $P-R$ 曲线被另一个学习器的曲线完全包住, 则可断言后者的性能优于前者. 例如, 上图中学习器 A 的性能优于学习器 C.

但如果曲线出现交叉的情况, 我们就需要使用其他方法来综合考虑查准率, 查全率的性能度量. 平衡点 (Break-Even Point, BEP) 是其中一个方法, 即 $P=R$ 时的取值, 据此, 我们可以说学习器 A 是优于学习器 B 的.

但 BEP 过于简化了, 我们更常用的是 $F1$ 度量. $F1$ 是基于查准率和查全率的调和平均:

不同应用对 $P$ 和 $R$ 的重视程度是不同的. 例如, 在商品推荐系统中, 为了尽可能少打扰用户, 我们更希望推荐内容确实是用户感兴趣的, 此时查准率更重要; 而在逃犯信息检索系统中, 更希望尽可能少漏掉逃犯, 此时查全率更重要. 所以, 我们引入 $F1$ 度量的一般形式 $→$ $F_\beta$

$\beta$ > 1时, 查全率有更大影响;

$\beta$ < 1时, 查准率有更大影响;

很多时候我们有多个二分类混淆矩阵, 例如进行多次训练/测试, 每次得到一个混淆矩阵. 或者我们执行多分类任务, 每两两类别的组合都对应一个混淆矩阵. 总之, 我们希望在 $n$ 个二分类混淆矩阵上综合考察 $P$ 和 $R$. 我们这里有两种做法:

  1. macro-P and macro-R

    一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率, 再计算平均值, 这样就得到宏查准率 (macro-P) 和宏查全率 (macro-R),以及相应的宏 $F1$ .

  2. micro-P and micro-R

    我们还可以先将各混淆矩阵的对应元素进行平均, 得到 $TP,FP,TN,FN$ 的平均值, 然后再基于这些平均值计算出:

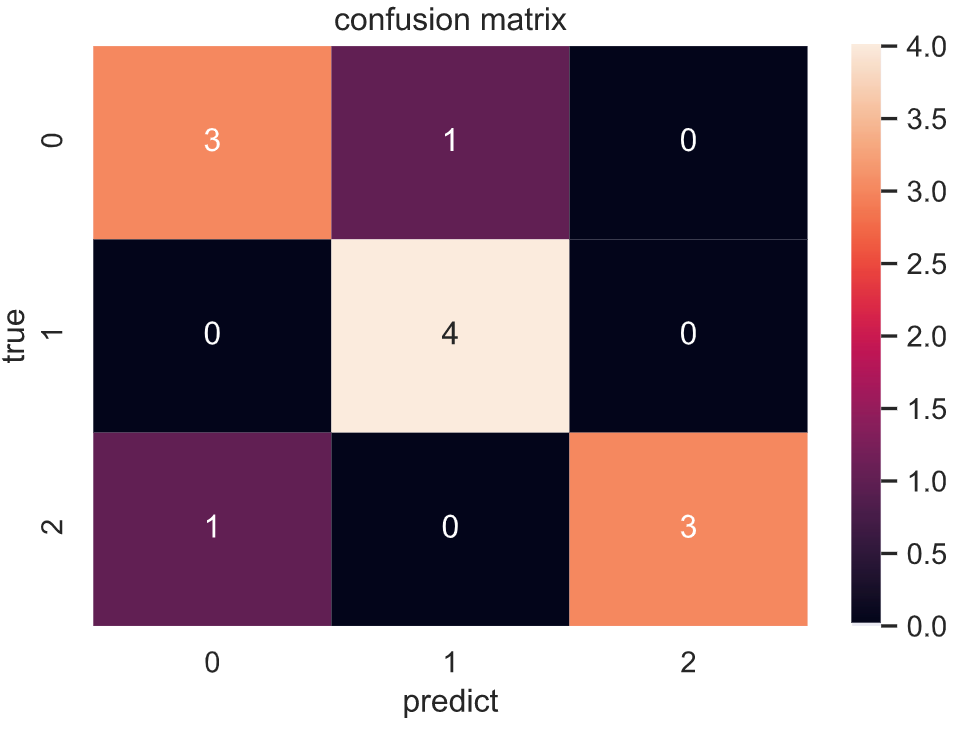
4.2.1 Plot Confusion Matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import seaborn as sns
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt

sns.set()
f,ax=plt.subplots()
y_true = [0,0,1,2,1,2,0,2,2,0,1,1]
y_pred = [1,0,1,2,1,0,0,2,2,0,1,1]
C2= confusion_matrix(y_true, y_pred,labels=[0, 1, 2])
# print(C2) #打印出来看看
sns.heatmap(C2,annot=True,ax=ax) #画热力图

ax.set_title('confusion matrix') #标题
ax.set_xlabel('predict') #x轴
ax.set_ylabel('true') #y轴

image-20201219043532565

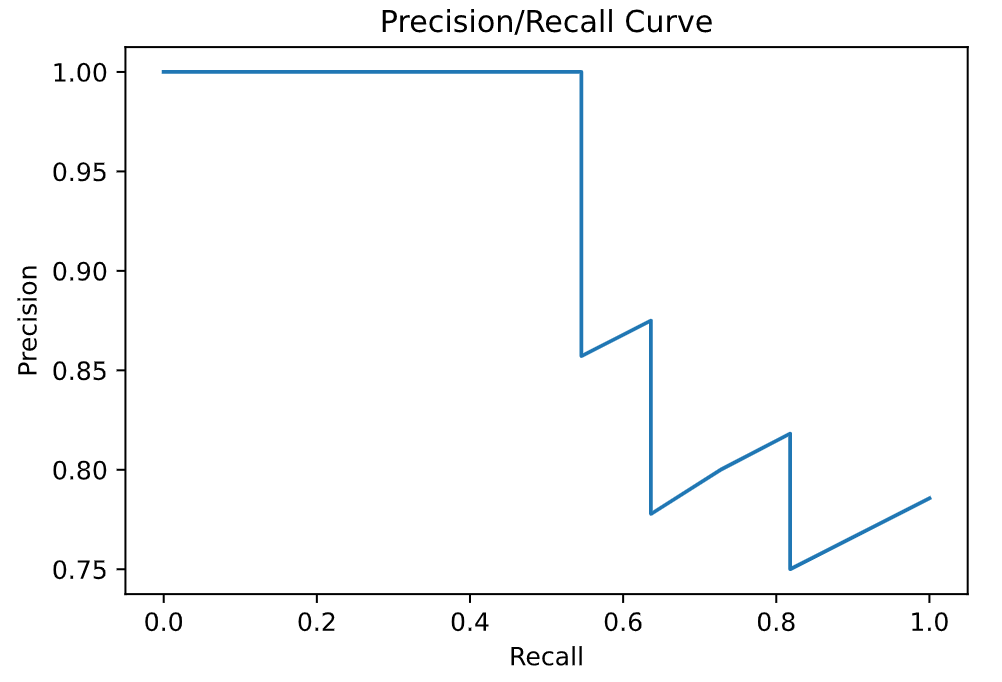
4.2.2 Plot PR Curve

根据学习器的预测结果对样本进行排序, 排在前面的是学习器认为最可能是正例的样本, 排在最后的是最不可能是正例的样本, 按此顺序逐个将样本作为正例预测, 则每次可以计算出当前的查全率、查准率，以查全率为横轴、查准率为纵轴做图, 得到的查准率-查全率曲线即为P-R曲线.

也就是说对每个样本预测其为正例的概率, 然后将所有样本按预测的概率进行排序, 然后依次将排序后的样本做为正例进行预测, 从而得到每次预测的查全率与查准率. 这个依次将样本做为正例的过程实际上就是逐步降低样本为正例的概率的域值, 通过降低域值, 更多的样本会被预测为正例, 从而会提高查全率, 相对的查准率可能降低, 而随着后面负样本的增加, 查全率提高缓慢甚至没有提升, 精度降低会更快.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#coding:utf-8
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
from sklearn.utils.fixes import signature

plt.figure("P-R Curve")
plt.title('Precision/Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')

#y_true为样本实际的类别，y_scores为样本为正例的概率
y_true = np.array([1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0])
y_scores = np.array([0.9, 0.75, 0.86, 0.47, 0.55, 0.56, 0.74, 0.62, 0.5, 0.86, 0.8, 0.47, 0.44, 0.67, 0.43, 0.4, 0.52, 0.4, 0.35, 0.1])
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

#print(precision)
#print(recall)
#print(thresholds)
plt.plot(recall,precision)
plt.show()

image-20201219042544752

4.3 ROC and AUC

很多学习器是为测试样本产生一个预测值, 然后将这个预测值与一个分类阈值 (threshold) 进行比较, 若大于阈值则分为正类, 否则为反类. 例如, 神经网络在一般情形下是对每个测试样本预测出一个 [0.0, 1.0] 之间的实值, 然后将这个值与 0.5 进行比较, 大于 0.5 则判为正例, 否则为反例. 这个实值或概率预测结果的好坏, 直接决定了学习器的泛化能力.

根据这个实值或概率预测结果, 我们可将测试样本进行排序, 最可能是正例的排在前面, 最不可能是正例的排在最后面. 这样, 分类过程就相当于在这个排序中以某个截断点 (cut point) 将样本分为两部分, 前一部分判作正例, 后一部分则判作反例. 在不同的任务中, 我们可以根据具体的任务绪论来采用不同的截断点.

  • 排序中靠前的位置进行截断 $\rightarrow$ 更重视 $Precision$
  • 排序中靠后的位置进行截断 $→$ 更重视 $Recall$
4.3.1 ROC

因此排序本身的好坏, 体现了综合考虑学习器在不同任务下的期望泛化性能的好坏. ROC 曲线则是从这个角度出发来研究泛化性能的有力工具.

ROC全称是“受试者工作特征”(Receiver Operating Characteristic)曲线, 它源于“二战”中用于敌机检测的雷达信号分析技术.

具体来说, 据说在二战期间, 军队中雷达兵的任务是通过观察显示屏的雷达信号来判断是不是有敌人来了, 在以下两种情况下显示屏上会有雷达信号:

  • 有敌机来袭 (真实情况下的正例)
  • 有飞鸟 (真实情况下的负例)

这个时候不同的雷达兵就可能会报出不同的结果:

  • 假如这个雷达兵比较谨慎, 只要有信号就报告有敌情 (可以看作更重视“查全率”), 就会增加误报的风险;
  • 假如这个雷达兵比较大胆, 只要有信号就认为是鸟 (可以看作更重视“查准率”), 就会增加漏报的风险;

这样就有了我们针对这个问题的“混淆矩阵”:

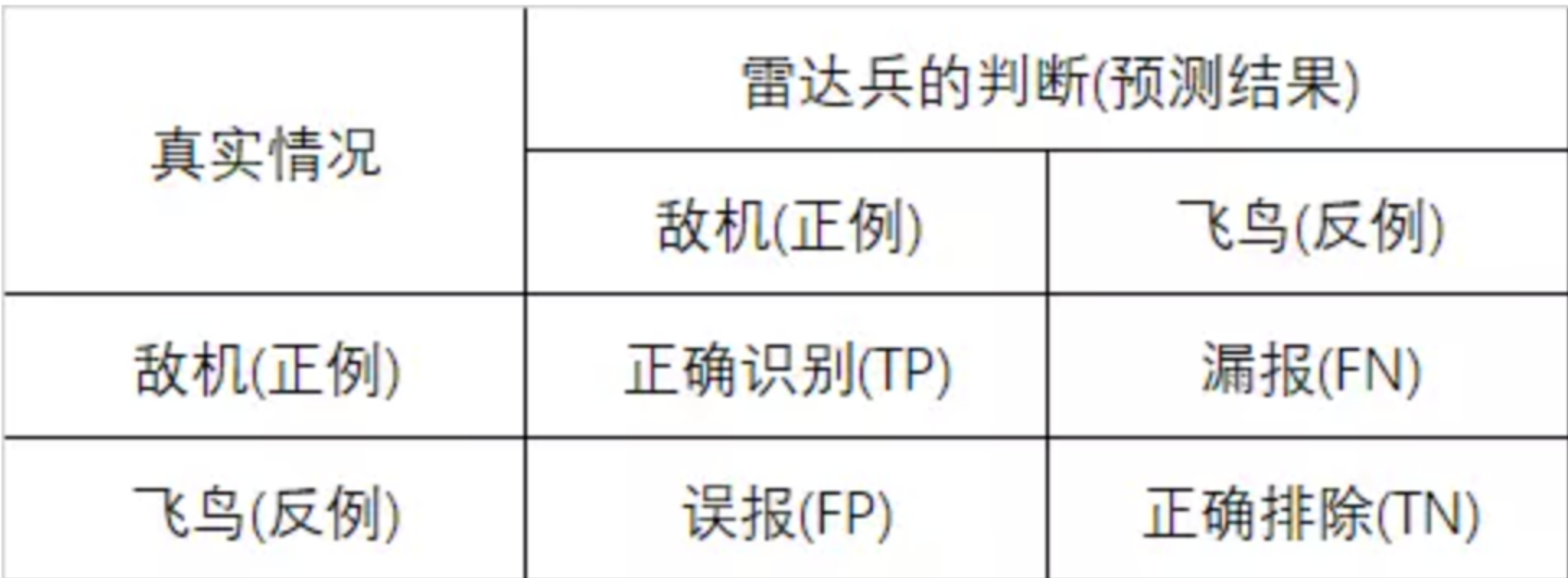
image-20201219003520752

理想情况下, 希望每个雷达兵能够好好研究飞机和飞鸟信号的区别, 进行准确的判断. 但是现实问题是, 每个雷达兵的判断标准不一, 谨慎的容易出现误报, 胆大的容易出现漏报. 针对以上问题, 雷达兵的上级管理者汇总了每个雷达兵的汇报特点, 尤其是他们的漏报和误报的概率, 并将这些概率基于二维坐标系绘制成一个图形:

  • 纵坐标为敏感性(真阳性率): 表示在所有敌人来袭(即真实情况为正例, TP+FN)的事件中, 每个雷达兵准确预报(即TP)的概率;
  • 横坐标为1-特异性(假阳性率): 表示在所有飞鸟信号(即真实情况为反例, TN+FP)中, 每个雷达兵预报错误(即FP)的概率;

每个雷达兵的预报标准不同, 所以得到的敏感性和特异性的组合也不同. 一个雷达兵的敏感性和特异性的组合正好在一条曲线上, 这条曲线就是ROC曲线. 到这里就不难理解ROC曲线为什么叫做“受试者工作特征”曲线了, 在这里受试者就是指雷达兵, 绘制这个曲线的目的就是观察雷达兵的工作特征, 所以叫做受试者工作特征曲线.

在机器学习中, 受试者就是我们的学习器了, 绘制曲线的目的就是观察学习器的工作性能. 不同的截断点会产生不同的 P-R 曲线或 ROC 曲线. 不同的算法模型对于同一个问题也会产生不同的 P-R 曲线或 ROC 曲线.

现在, 我们来研究如何绘制 ROC 曲线.

与我们之前介绍的 P-R 曲线类似, 我们根据学习器的预测结果对样例进行排序, 按此顺序逐个把样本作为正例进行预测, 每次计算出两个重要量的值:

  • 真正例率 (True Positive Rate), 也可以称为灵敏度 (Sensitivity)

  • 假正例率 (False Positive Rate), 也可以称为 $1-Specificity$ (特异度)

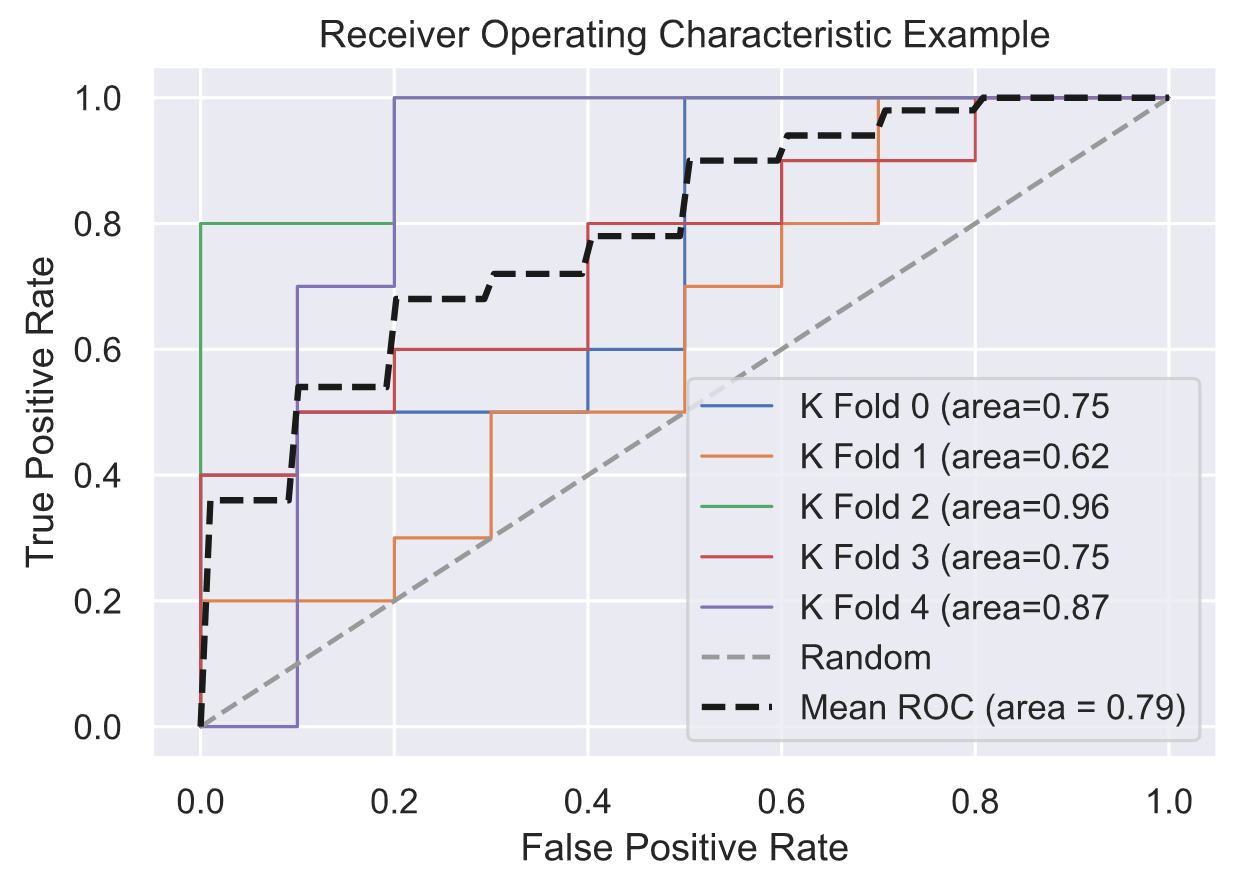
以FPR作为横轴, TPR作为纵轴作图, 就得到了“ROC曲线”, 显示ROC曲线的图叫做“ROC图”, 如下所示:

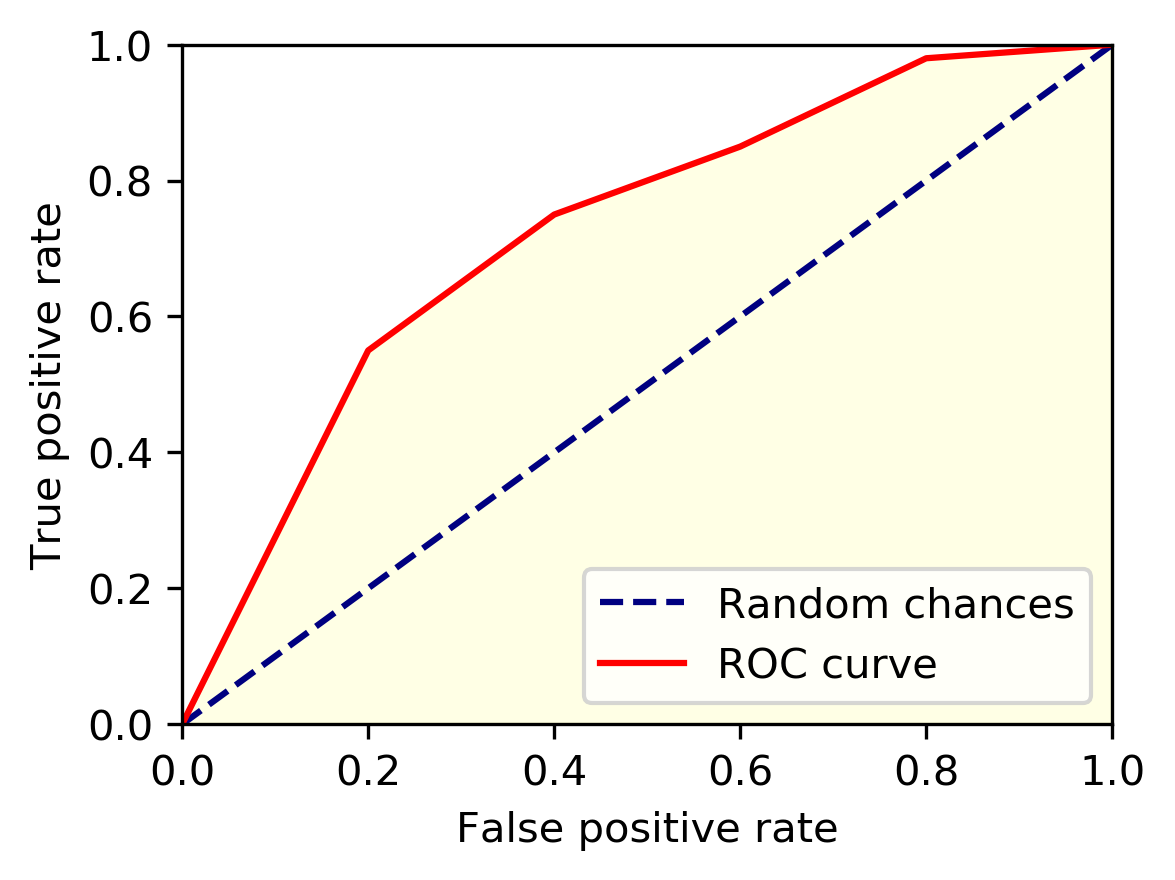
ROC Curve Transforms the Way We Look at a Classification Problem | by Huy Bui | Towards Data Science

对 ROC 曲线的几点解释:

  1. 图中的对角线 (图中的虚线), 对应随机猜测模型, 这种模型没有任何价值;
  2. $ROC$ 曲线越靠近左上角, 性能越好；
  3. 点(0,1) (左上角), 对应于将所有正例排在所有反例之前的“理想模型”, 也就是 FPR=0,TPR=1, 结合上面的公式, 可以得到这时 FP=0,FN=0 模型对所有的样本分类都正确, 也就是将真实为正的预测为正, 真实为反的预测为反.
  4. $ROC$ 曲线与 $P-R$ 曲线不一样的地方在于, 当正反样例分布发生剧烈变化的时候: ROC曲线的形状基本能够保持不变, P-R曲线的形状一般会发生剧烈变化.

对于“理想模型”, 即将所有正例排在所有反例之前, 在画 ROC 曲线过程中, 由于前 $m^+$ 个样例均为真正例, 即从 $(0,0)$ 一直沿纵轴方向增加 $m^+$ 次, 每次增加 $\frac{1}{m^+}$, 到达坐标 (0,1); 接下来 $m^-$ 个样例均为假正例, 即一直沿着横坐标走, 轨迹为从 $(0,0)$ 至 $(1,1)$.

对于“随机猜测”模型, 即根据预测结果对样例进行排序基本是正例和反例均匀分布 (假如正例个数等于反例个数, 则应该是一个正例一个反例), 在画 ROC 曲线过程中, 向纵方向走一步, 然后向横轴方向走一步, 因此轨迹为从 $(0,0)$ 至 $(1,1)$.

现实任务中, 通常是利用有限个测试样例来绘制ROC图, 此时仅能获得有限个(FPR,TPR)坐标对, 无法产生图中光滑的ROC曲线,绘制过程如下:

  1. 给定 $m^+$ 个正例和 $m^-$ 个反例, 根据学习器预测结果对样例进行排序;
  2. 设置不同的分类阈值:
    • 把分类阈值设为最大, 即把所有样例均预测为反例, 此时TPR=FPR=0. 在坐标(0,0)处标记一个点.
    • 将分类阈值依次设为每个样例的预测值, 即依次将每个样例划分为正例. 设前一个标记点坐标为 $(x,y)$:
      • 当前若为真正例 (TP), 则对应标记点的坐标为 $(x,y+\frac{1}{m^+})$
      • 当前若为假正例(FP), 则对应标记点的坐标为 $(x+\frac{1}{m^-},y)$
    • 最后用线段连接相邻点即得 ROC曲线;
4.3.2 AUC

进行学习器比较时, 与P-R图类似:

  • 若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”, 则可断言后者的性能优于前者;
  • 若两个学习器的ROC曲线发生交叉, 则难以一般性地断言两者哪个更优. 此时如果一定要进行比较, 则较为合理的判据是: 比较ROC曲线下的面积, 即AUC(Area Under ROC Curve).

从定义可知, AUC可通过对ROC曲线下各部分的面积求和而得. 我们假定 ROC 曲线是有坐标为 $\{(x_1,y_1),(x_2,y_2),…,(x_m,y_m)\}$ 的点按序连接而形成, 参见图 (b), 则 AUC 可以估算为:

4.3.3 What are they?

看书到此, 可能感觉也知道了什么是 ROC、什么是 AUC, 却又感觉没有理解其含义.

先梳理四个概念: 真正例率 TPR、假正例率 FPR、真反例率 TNR、假反例率 FNR，各概念的定义如下图所示:

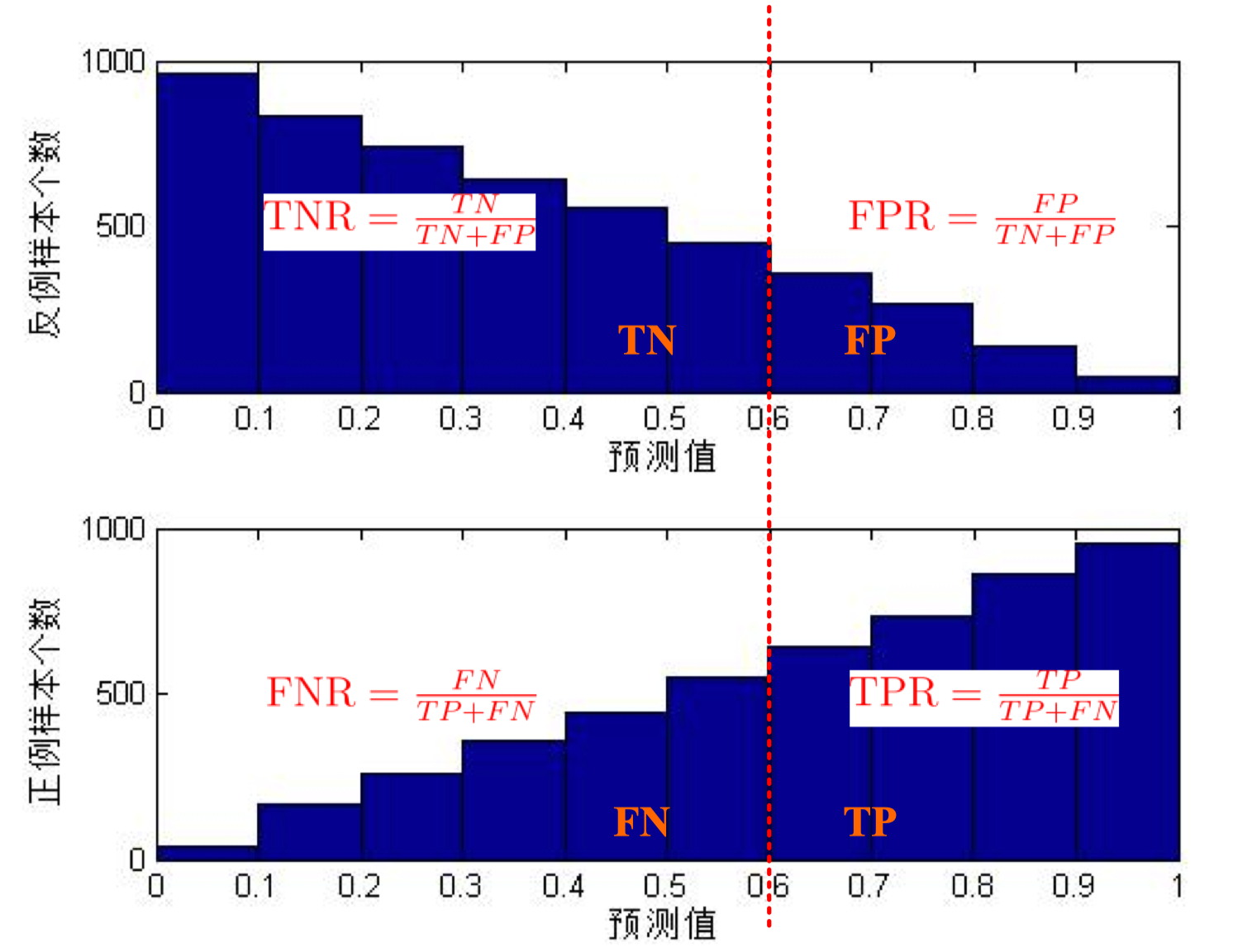
image-20201004150516758

注: 上图由如下步骤绘出, 首先随机生成了 10000 个样本预测值 (位于 0~1 之间); 然后将每个样本随机指派为正例或反例, 样本预测值越大被指派为正例的概率越大, 反之被指派为反例的概念越大, 指派结果作为对应的 10000 个样本真实标记; 最后将 0~1 划分为 10 个区间, 分别统计每个区间内包含的正例个数和反例个数, 并用直方图表示.

由上图可以看出, 无论分类域值设置为多少, 肯定都会有样本被分类错误. 这也是实际当中最常见的情形. 设当前分类域值等于 0.6, 则可以分别得到真正例、假正例、真反例、 假反例的个数 TP、FP、TN、FN, 进而可依次计算出真正例率 TPR、假正例率 FPR、真反 例率 TNR、假反例率 FNR.

实际上, TPR、FPR、TNR、FNR 就是把混淆矩阵中的四个值均除以对应的行元素之和, 而行元素之和分别表示正例样本个数和反例样本个数, 因此还可以使用条件概率做如下解释:

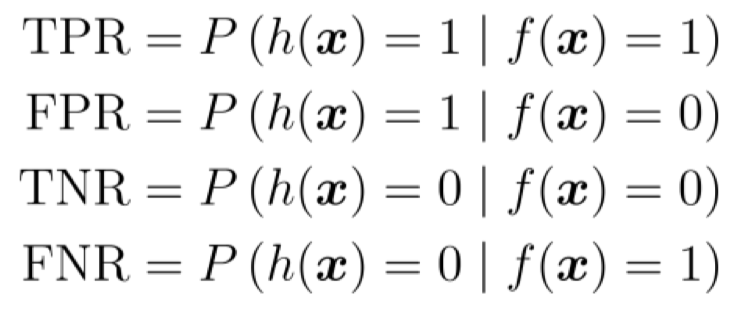
image-20201004151407009.png

接下来, 我们对 ROC 和 AUC 做几条解释:

  1. 由上图还可以看出, 绘制 ROC 曲线时使用的 TPR 和 FPR, 都是基于分类域值右侧 (大于分类域值) 的样本.
  2. 由式(2.21)可知, $\ell_{rank}$ 表示任取一对正例和反例, 正例预测值小于反例预测值的概率 (简单起见可以暂不考虑预测值相等的情况); 这是因为分母表示所有正例和反例组合对的个数, 分子的求和项表示正例和反例组合对中, 正例预测值小于反例预测值的组合对个数. 显然, 这个概率越小越好 (正例预测值应该大于反例预测值).
  3. $AUC+\ell_{rank}=1$, 因此 AUC 表示任取一对正例和反例, 正例预测值大于反例预测值的概率. 显然, 这个概率越大越好.
  4. 按西瓜书所述, ROC 曲线绘制的过程. 其实就是将上图中分类域值从右往左（即从 1 到 0）滑动一遍, 依次记录每个域值时的 TPR 和 FPR, 描点画线即可.
  5. ROC 曲线的绘制所使用的样本集应该是测试集, 即 ROC 曲线上的每个点表示了当取不同分类域值时, 分类器泛化性能的度量 (正例样本的精度 TPR 和反例样本的错误率 FPR).

AUC的优势：AUC的计算方法同时考虑了分类器对于正例和反例的分类能力, 在样本不均衡的情况下, 依然能够对分类器作出合理的评价. (即AUC对样本类别是否均衡并不敏感, 这也是不均衡样本通常用AUC评价分类器性能的一个原因)

例如：在反欺诈场景, 设非欺诈类样本为正例, 反例占比很少(假设为0.1%):

  • 如果使用准确率评估, 把所有样本预测为正, 便可以获得99.9%的准确率;
  • 但是如果使用AUC, 把所有样本预测为正例, TPR=FPR=1, AUC仅为0.5, 成功规避了样本不均衡带来的问题;
4.4.4 Plot Curve
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Import the data to play with 
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 将数据二分类
X,y = X[y!=2],y[y!=2]

# 增加噪声特征
random_state = np.random.RandomState(0)
n_samples,n_features = X.shape
X = np.c_[X,random_state.randn(n_samples,200*n_features)]

cv = StratifiedKFold(n_splits=5) #导入该模型，后面将数据划分5份
classifier = svm.SVC(kernel='linear',probability=True,random_state=random_state)

# 画平均ROC曲线的两个参数
mean_tpr = 0.0      # 用来记录画平均ROC曲线的信息
mean_fpr = np.linspace(0,1,100)
cnt = 0
for i, (train,test) in enumerate(cv.split(X,y)):
    cnt += 1
    probas_ = classifier.fit(X[train],y[train]).predict_proba(X[test]) # 训练模型后预测每条样本得到两种结果的概率
    fpr,tpr,thresholds =roc_curve(y[test],probas_[:,1])  # 该函数得到伪正例、真正例、阈值，这里只使用前两个

    mean_tpr += np.interp(mean_fpr,fpr,tpr) # 插值函数:两点之间的线性取值

    roc_auc = auc(fpr,tpr)
    plt.plot(fpr,tpr,lw=1,label="K Fold {0} (area={1:.2f}".format(i,roc_auc))

plt.plot([0,1],[0,1],'--',color=(0.6,0.6,0.6),label="Random") # 画对角线

mean_tpr /= cnt # 求均值
mean_tpr[0] = 0.0 # 将第一个真正例
mean_tpr[-1] = 1.0 # 坐标最后一个点为（0,1） 
mean_auc = auc(mean_fpr, mean_tpr)

plt.plot(mean_fpr, mean_tpr, 'k--',label='Mean ROC (area = {0:.2f})'.format(mean_auc), lw=2)
plt.xlim([-0.05, 1.05])     # 设置x、y轴的上下限，设置宽一点，以免和边缘重合，可以更好的观察图像的整体
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')    # 可以使用中文，但需要导入一些库即字体
plt.title('Receiver Operating Characteristic Example')
plt.legend(loc="lower right")
plt.show()

效果如下:

image-20201219053227939