详解线性回归(Linear Regression)

1. Notation

给定由 d 个属性描述的示例 $x=(x_1;x_2;…;x_d)$, 其中 $x_i$ 是 $x$ 在第 $i$ 个属性上的取值, 线性模型 (linear model) 试图学得一个通过属性的线性组合来进行预测的函数, 即

$$f(x)=w_1x_1+w_2x_2+...+w_dx_d+b$$

一般用向量形式写成

$$f(x)=w^Tx+b$$

其中 $w=(w_1;w_2;…;w_d)$

注: 我们可以观测到 $x,w$ 的向量表示中都有分号 ;. 这说明其是一个列向量. 因此 $x^T,w^T$ 则是行向量.

2. Standard Linear Regression

2.1 Simple LR

这种情况下, 输入属性的数目只有一个. 为便于讨论, 此时我们忽略关于属性的下标, 即 $D=\{(x_i,y_i)\}_{i=1}^m$, 其中 $x_i\in\mathbb{R}$.

简单线性回归试图学得

$$f(x_i)=wx_i+b,\quad thus \ f(x_i)\approx y_i$$

如何确定 $w$ 和 $b$ 呢? 我们可以通过最小化均方误差 (mean squared error, MSE) 来得到 $w$ 和 $b$, 即

基于均方误差最小化来进行模型求解的方法称为 “最小二乘法 (least square method)”. 在线性回归中, 最小二乘法就是试图找到一条直线, 使所有样本到直线上的欧氏距离之和最小.

求解 $w$ 和 $b$ 使 $E_{(w,b)}=\frac{1}{2}\sum_{i=1}^m(y_i-wx_i-b)^2$ 最小化的过程, 称为线性回归模型的最小二乘 “参数估计 (parameter estimation)”. 我们可以将 $E_{(w,b)}$ 分别对 $w$ 和 $b$ 求导, 得到

$$\frac{\delta E(w,b)}{\delta w}=\sum_{i=1}^m(y_i-wx_i-b)x_i \\ \frac{\delta E(w,b)}{\delta b}=\sum_{i=1}^m(y_i-wx_i-b)$$

然后令上面两个式子为零可得到 $w$ 和 $b$ 最优解的闭式 (closed-form) 解.

注:

这里 $E_{(w,b)}$ 是关于 $w$ 和 $b$ 的凸函数, 当它关于 $w$ 和 $b$ 的导数均为零时, 我们能得到 $w$ 和 $b$ 的最优解.

对于曲线 $[a,b]$ 上定义的函数 $f$, 若它对区间的任意两点 $x_1,x_2$ 均有 $f(\frac{x_1+x_2}{2})\le\frac{f(x_1)+f(x_2)}{2}$, 则称 $f$ 为区间 $[a,b]$ 上的凸函数.

对实数集上的函数, 可以通过求二阶导数来判别. 若二阶导数在区间上非负, 则称为凸函数; 若二阶导数在区间上恒大于 0, 则称为严格凸函数.

2.2 Multivariate LR

在实际回归问题中, 更一般的情形是如本节开头的数据集 $D$, 样本由 $d$ 个属性描述. 此时我们试图学得

$$f(x_i)=w^Tx_i,\quad thus \ f(x_i)\approx y_i$$

注: 我们此时将 $b$ 包括进了 $w$.

那我们如何求解最优的 $w$ 呢?

我们可以同样适用均方误差来求解, 即

$$f(w)=\frac{1}{2}\sum_{i=1}^m(y_i-x_i^Tw)^2$$

对于上述式子 $f(w)$ 可以通过梯度下降等方法得到最优解. 但是使用矩阵表示将会是的求解和程序更为简单:

$$f(w)=(y-Xw)^T(y-Xw)$$

将 $f(w)$ 对 $w$ 求导可得:

$$\frac{\delta f(w)}{\delta w}=-2X^T(y-Xw)$$

使其等于0, 我们便可得到:

$$\hat{w}=(X^TX)^{-1}X^Ty$$

然而在现实操作中, 会出现 $X^TX$ 不可逆的情况. 如果这种情况出现了, 我们一般考虑以下两种情况:

• 移除冗余特征, 一些特征存在线性依赖;
• 特征太多时, 要删除一些特征. 例如 (m<n), 对于小样本数据使用正则化;

2.3 Probabilistic Explanation

关于: 为何在进行线性回归时, 选择用最小二乘拟合 (距离的平方和) 来进行, 而不是选用其他的模型 (比如三次方或四次方)?

我们更新一下假设函数, 使之变为:

$$y_{i}=\theta^Tx_{i}+ε_{i}$$

其中, $ε_{i}$ 是误差项, 表示未捕获的特征 (unmodeled effects), 比如房子存在壁炉也影响价格, 或者其他的一些随机噪音 (random noise).

一般，会假设误差项$ε_{i}∼N(0,σ^2)$ (满足正态分布), 也就是:

关于为什么假设正态分布的解释:

1. 便于数学运算;
2. 很多独立分布的变量之间相互叠加后会趋向于正态分布 (中心极限定理), 在大多数情况下能成立;

$$P(ε_{i})=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(ε_{i})^2}{2\sigma^2})$$

所以, $y^{(i)}$ 的后验分布:

$$P(y_{i}|x_i;\theta)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})\sim N(\theta^Tx_i,\sigma^2)$$

之后, 进行极大似然估计 (MLE): $\max L(θ)$, 即选择合适的 $θ$, 使得$y^{(i)}$ 对于 $x^{(i)}$ 出现的概率最高 (有一些存在即合理的感觉), 其中 $L(θ)$ 的定义如下:

$$L(\theta)=P(y|x;\theta)=\prod_{i=1}^{m}P(y_i|x_i;\theta)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}}\exp(-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})$$

那么, 为了计算方便, 我们取对数:

$$LL(\theta)=\log L(\theta)=\sum_{i=1}^m\log P(y_i|x_i;\theta)=m\cdot\log\frac{1}{\sqrt{2\pi}\sigma}-\sum_{i=1}^m\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2}$$

于是, 极大似然估计变为最小化:

$$\sum_{i=1}^m\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2}$$

也即之前线性回归所需进行最小二乘拟合的 $J(θ)$.

2.4 Code

数据集来源: http://archive.ics.uci.edu/ml/datasets/Abalone

import numpy as np
import matplotlib.pyplot as plt


def load_data(filename):
    ''' 加载数据
    '''
    X, Y = [], []
    with open(filename, 'r') as f:
        for line in f:
            splited_line = [float(i) for i in line.split()]
            x, y = splited_line[: -1], splited_line[-1]
            X.append(x)
            Y.append(y)
    X, Y = np.matrix(X), np.matrix(Y).T
    return X, Y

def standarize(X):
    ''' 中心化 & 标准化数据 (零均值, 单位标准差)
    '''
    std_deviation = np.std(X, 0)
    mean = np.mean(X, 0)
    return (X - mean)/std_deviation

def std_linreg(X, Y):
    xTx = X.T*X
    if np.linalg.det(xTx) == 0:
        print('xTx is a singular matrix')
        return
    return xTx.I*X.T*Y

def get_corrcoef(X, Y):
    # X Y 的协方差
    cov = np.mean(X*Y) - np.mean(X)*np.mean(Y)
    return cov/(np.var(X)*np.var(Y))**0.5

if '__main__' == __name__:
    # 加载数据
    X, Y = load_data('abalone.txt')
    X, Y = standarize(X), standarize(Y)
    # 增加 bias
    X = np.insert(X,0,1,axis=1)
    w = std_linreg(X, Y)
    Y_prime = X*w

    print('w: {}'.format(w))

    # 计算相关系数
    corrcoef = get_corrcoef(np.array(Y.reshape(1, -1)),
                            np.array(Y_prime.reshape(1, -1)))
    print('Correlation coeffient: {}'.format(corrcoef))

在例子中我们计算了相关系数, 这是用来判断模型预测能力好或坏的指标. 换句话说, 我们需要计算得到的 $y$ 的值向量与实际 $y$ 值向量的匹配程度, 也就是计算相关系数 Correlation Coefficient. 相关系数的计算公式:

$$r(X,Y)=\frac{Cov(X,Y)}{\sigma_X\sigma_Y}$$

也就是两个数据序列的协方差并除上各自的标准差, 本质上就是一种剔除了两个变量量纲影响, 标准化后的特殊协方差. 而协方差便是衡量两个变量变化趋势是否相似的一种方法, 是同向变化(同时变大或变小)还是反向变化(一个变大一个变小), 同向或者反向的程度如何, 计算公式如下:

$$Cov(X,Y)=E[(X-E[X])(Y-E[Y])]$$

通过公式可以看出, 如果对于向量中的每个 $x,y$ 同时大于或同时小于各自的期望值, 协方差为正, 相反则为负. 可见如果协方差越大相似程度就越高, 协方差越小相似程度就越小. 也可以看到如果 $X,Y$ 相同, 协方差就是方差, 也就是方差是一种特殊情况下的协方差.

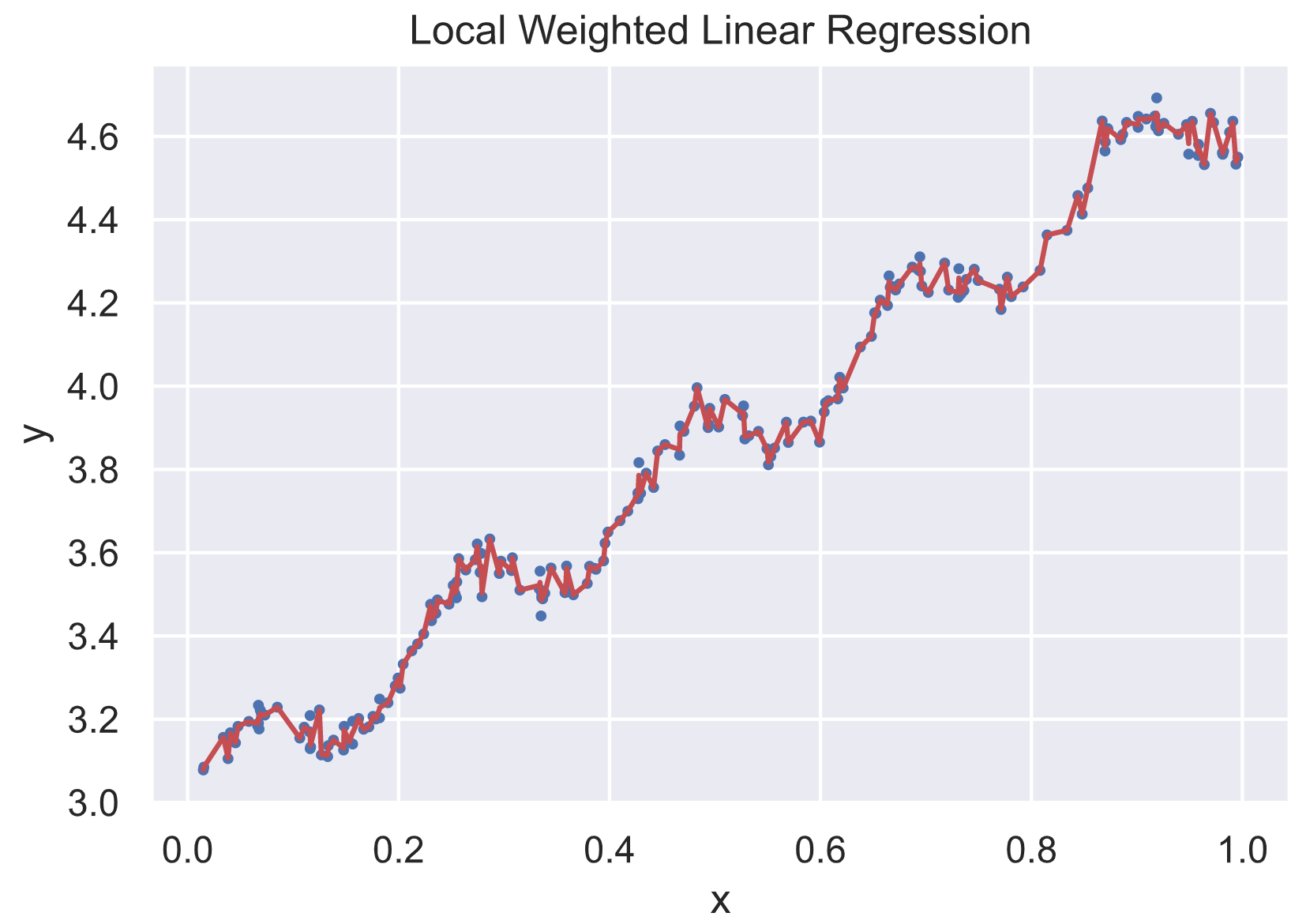
3. Local Weighted Linear Regression

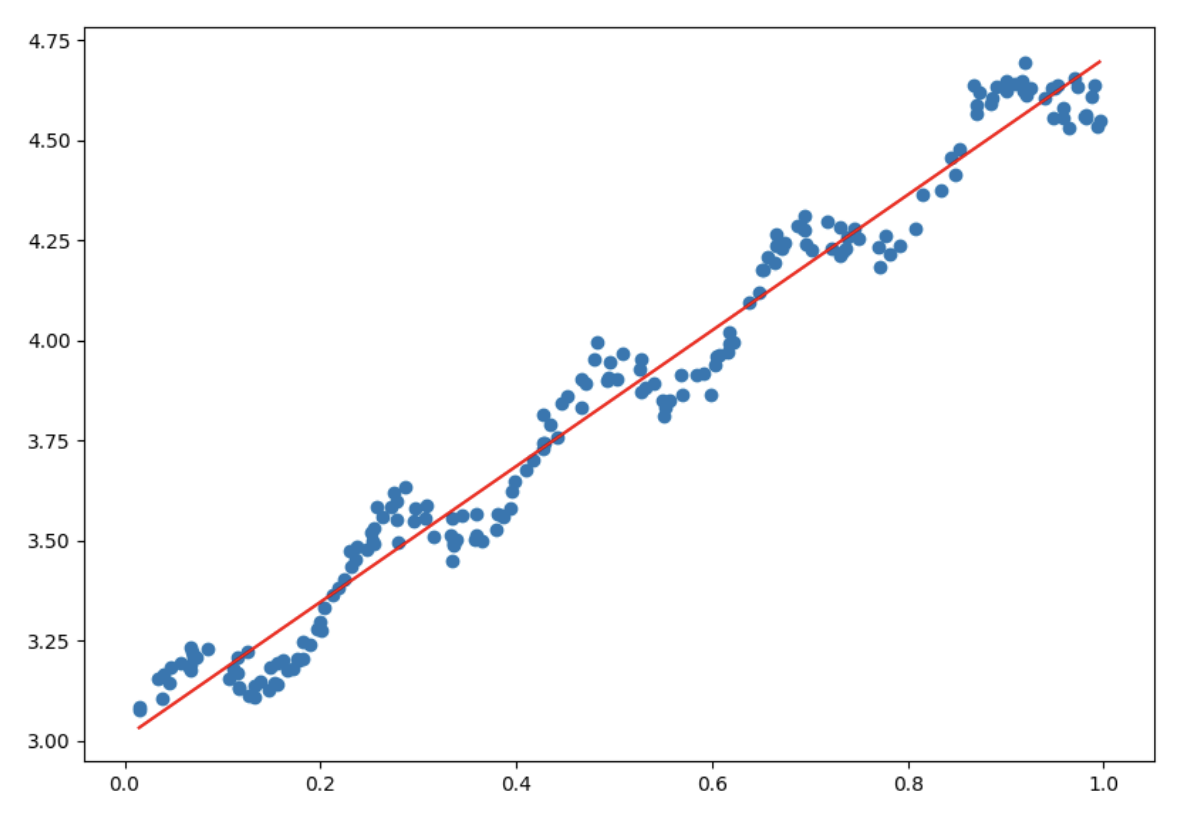
上面的数据点事通过公式 $y=3+1.7x+0.1\sin(30x)$ 添加噪声生成的数据, 而标准的线性回归是一种无偏差估计, 在计算所有点的时候都是无偏差的计算误差并通过优化方法优化误差, 如果针对不同的点能够对误差进行调整便可以一定程度上避免标准线性回归带来的欠拟合现象.

也就是引入偏差来降低预测的均方误差, 本部分总结下局部加权线性回归的方法. 当我们获取某个 $x$ 的预测值的时候，我们需要计算回归系数 $w$, 但是如果针对样本中的数据, 距离 $x$ 越近我们就给个越大的权重, 如果距离越远就给一个小的权重, 这样就会使得针对 $x$ 的预测值 $y_{predict}$ 能够更贴合样本数据.

当我们需要对数据点 $x$ 相应的目标值进行预测的时候, 我们需要给样本中的每个点赋予一个权重值 $w_i$ (为了区分权重和回归系数，在这里用 $\theta$ 表示回归系数, $w$ 表示权重), 那么平方误差的表达式就变成:

$$f(\theta)=\sum_{i=1}^mw_i(y_i-x_i^T\theta)^2$$

通过矩阵可以表示成:

$$f(\theta)=(y-X\theta)^TW(y-X\theta)$$

计算 $f(\theta)$ 对 $\theta$ 求导可得:

$$\frac{\delta f(\theta)}{\delta\theta}=-2X^TW(y-X\theta)=0 \\ \hat{\theta}=(X^TWX)^{-1}X^TWy$$

通过上面的公式, 对于任意给定的未知数据可以计算出对应的回归系数 $\theta$, 并得到相应的预测值 $y_{predict}$, 其中 $W$ 是一个对角矩阵, 对角线上的元素 $w_{ii}$ 对应样本点 $x_i$ 的权重值.

3.1 Gaussian Kernel

那么权重的表达式又是怎样的呢, 我们需要赋予距离给定 $x$ 的样本点的权重越高, LWLR 使用核来对附近的点赋予更高的权重, 最常用的是高斯核函数, 对应表达式如下:

$$w_{ii}=\exp(\frac{|x_i-x|^2}{-2k^2})$$

通过公式可以看到如果 $x_i$ 距离 $x$ 的距离越小, $w_{ii}$ 就会越大, 其中参数 $k$ 决定了权重的大小. $k$ 越大权重差距就越小, $k$ 越小权重差距就很, 大, 仅有局部的点参与进回归系数的求取, 其他距离较远的权重都趋近于零. 如果 $k$ 趋近于无穷大, 所有权重都趋近于1, $W$ 也就近似等于单位矩阵, 局部加权线性回归变成标准的无偏差线性回归, 会造成欠拟合的现象. 当 $k$ 很小的时候, 距离较远的样本点无法参与回归参数的求取, 会造成过拟合的现象.

3.2 Code

数据集: https://raw.githubusercontent.com/PytLab/MLBox/master/linear_regression/ex0.txt

import numpy as np 
import matplotlib.pyplot as plt

def load_data(filename):
    """
    加载数据
    """
    X, Y = [], []
    with open(filename, 'r') as f:
        for line in f:
            splited_line = [float(i) for i in line.split()]
            x, y = splited_line[: -1], splited_line[-1]
            X.append(x)
            Y.append(y)
    X, Y = np.matrix(X), np.matrix(Y).T
    return X, Y

def get_corrcoef(X, Y):
    """
    X Y 的协方差
    """ 
    cov = np.mean(X*Y) - np.mean(X)*np.mean(Y)
    return cov/(np.var(X)*np.var(Y))**0.5

def lwlr(x,X,Y,k):
    """
    局部加权线性回归, 给定一个点, 获取相应权重矩阵并返回回归系数
    """
    n_samples,_ = X.shape

    # 创造针对 x 的权重矩阵
    W = np.matrix(np.zeros((n_samples,n_samples)))
    for i in range(n_samples):
        xi = np.array(X[i])
        x = np.array(x)
        W[i, i] = np.exp((np.linalg.norm(x - xi))/(-2*k**2))

    # 获取此点相应的回归系数

    xWx = X.T*W*X
    if np.linalg.det(xWx) == 0:
        print('xWx is a singular matrix')
        return
    w = xWx.I*X.T*W*Y

    return w

if '__main__' == __name__:
    k = 0.1

    X, Y = load_data('ex0.txt')
    
    y_prime = []
    for x in X.tolist():
        w = lwlr(x, X, Y, k).reshape(1, -1).tolist()[0]
        y_prime.append(np.dot(x, w))

    corrcoef = get_corrcoef(np.array(Y.reshape(1, -1)), np.array(y_prime))
    print('Correlation coefficient: {}'.format(corrcoef))

    fig = plt.figure()
    ax = fig.add_subplot(111)

    # 绘制数据点
    x = X[:, 1].reshape(1, -1).tolist()[0]
    y = Y.reshape(1, -1).tolist()[0]
    ax.scatter(x, y,s=5)

    # 绘制拟合直线
    x, y = list(zip(*sorted(zip(x, y_prime), key=lambda x: x[0])))
    ax.plot(x, y, c='r')

    plt.show()

1) 当 k=0.5, 基本上就是无偏差的标准线性回归

Correlation coefficient: 0.9869292425124011

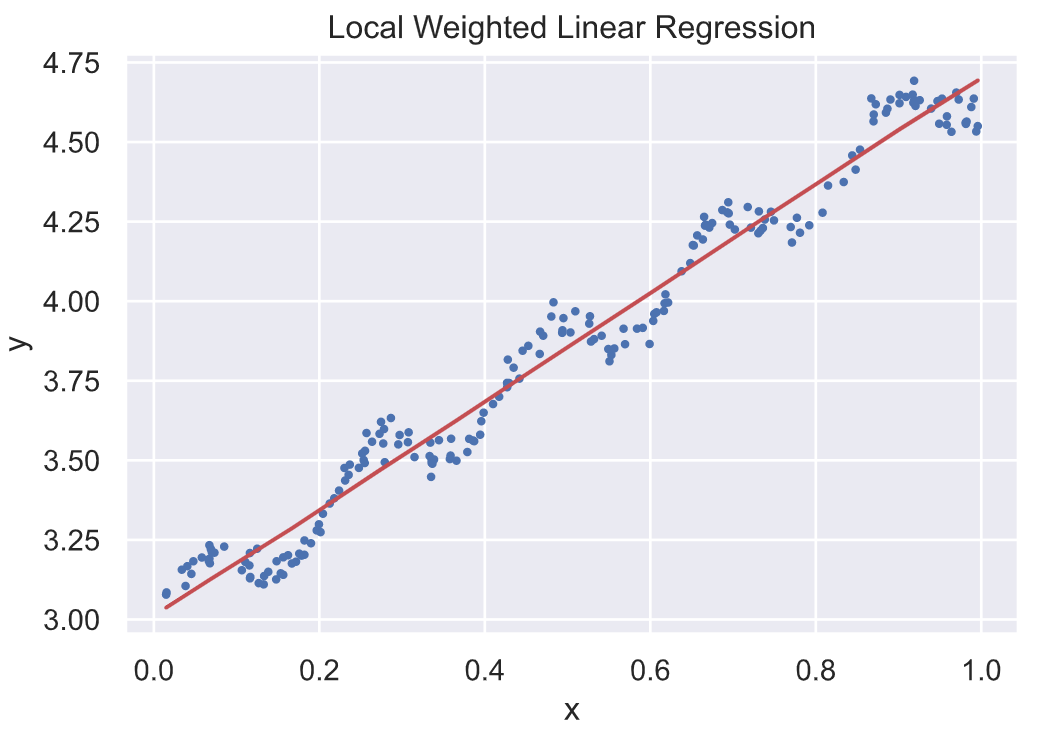
2) 当 k=0.1, 可以较好的反应数据的潜在规律

Correlation coefficient: 0.9978904026105981

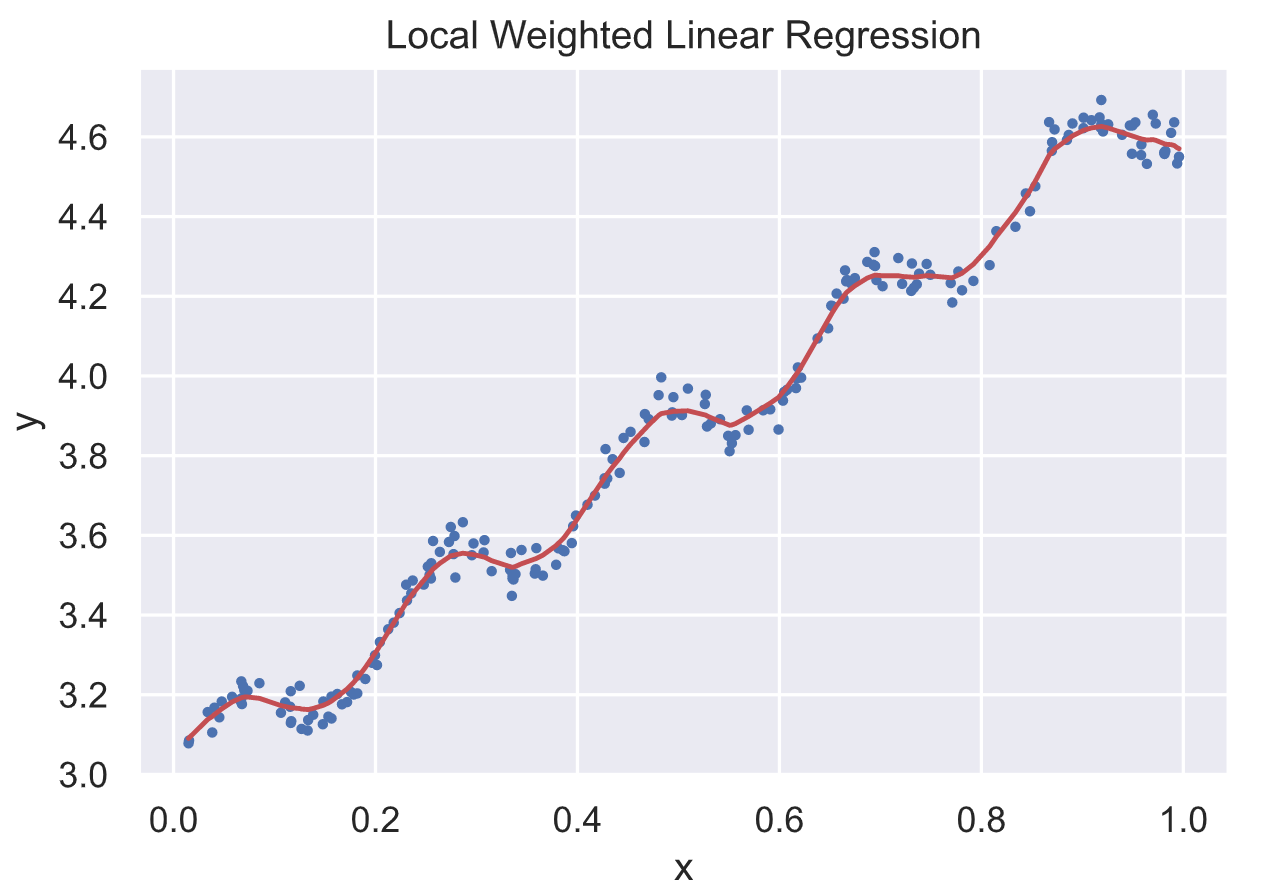
3) 当 k=0.02, 拟合所得曲线较多的考虑了噪声数据导致过拟合的现象

Correlation coefficient: 0.9998256819814548

4. Ridge Regression

我们已经知道标准线性回归的参数可以通过 $w=(X^TX)^{-1}X^Ty$ 进行求解. 但是 $X^TX$ 不一定总是可逆. 在种情况下, 我们需要对最初的标准线性回归做一定的变化使原先无法求逆的矩阵变得非奇异, 使得问题可以稳定求解. 我们可以通过缩减的方式来处理这些问题例如岭回归和LASSO.

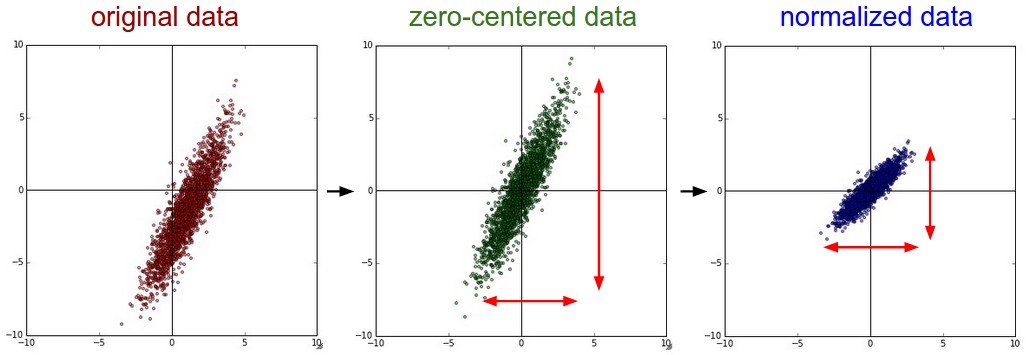
我们首先介绍一下数据的中心化和标准化, 在回归问题和一些机器学习算法中通常要对原始数据进行中心化和标准化处理, 也就是需要将数据的均值调整到0, 标准差调整为1, 计算过程很简单就是将所有数据减去平均值后再除以标准差:

$$x_i'=\frac{x_i-\mu}{\sigma}$$

之所以需要进行中心化其实就是个平移过程, 将所有数据的中心平移到原点. 而标准化则是使得所有数据的不同特征都有相同的尺度Scale, 这样在使用梯度下降法以及其他方法优化的时候不同特征参数的影响程度就会一致了.

如下图所示，可以看出得到的标准化数据在每个维度上的尺度是一致的:

现在我们开始介绍岭回归 (Ridge Regression)

标准最小二乘法优化问题:

$$f(w)=\sum_{i=1}^m(y_i-x_i^Tw)^2$$

也可以通过矩阵表示:

$$f(w)=(y-Xw)^T(y-Xw)$$

得到归回归系数为:

$$\hat{w}=(X^TX)^{-1}X^Ty$$

这个问题解存在且唯一的条件就是 $X$ 列满秩: $rank(X)=dim(X)$

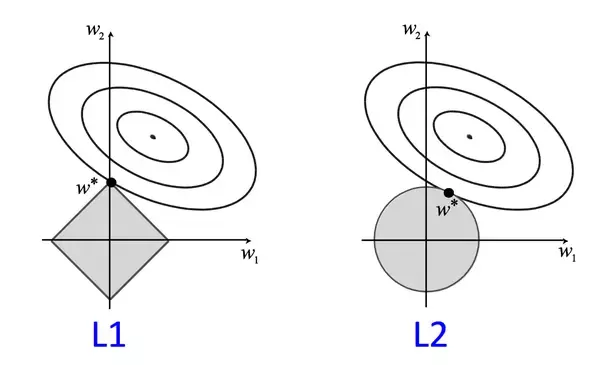
即使 $X$ 列满秩, 但是当数据特征中存在共线性, 即相关性比较大的时候, 会使得标准最小二乘求解不稳定, $X^TX$ 的行列式接近零, 计算 $X^TX$ 的时候误差会很大. 这个时候我们需要在 cost function 上添加一个惩罚项 $\lambda\sum_{i=1}^nw_i^2$, 也就是 L2 正则化. 这个时候的cost function的形式就为:

$$f(x)=\sum_{i=1}^m(y_i-x_i^Tw)^2+\lambda\sum_{i=1}^nw_i^2$$

将岭回归系数用矩阵的形式表示:

$$\hat{w}=(X^TX+\lambda I)^{-1}X^Ty$$

可以看到，就是通过将 $X^TX$ 加上一个类单位矩阵变成非奇异矩阵并可以进行求逆运算. 更多正则化相关内容, 可以查看我的相关文章.

岭回归的一些性质

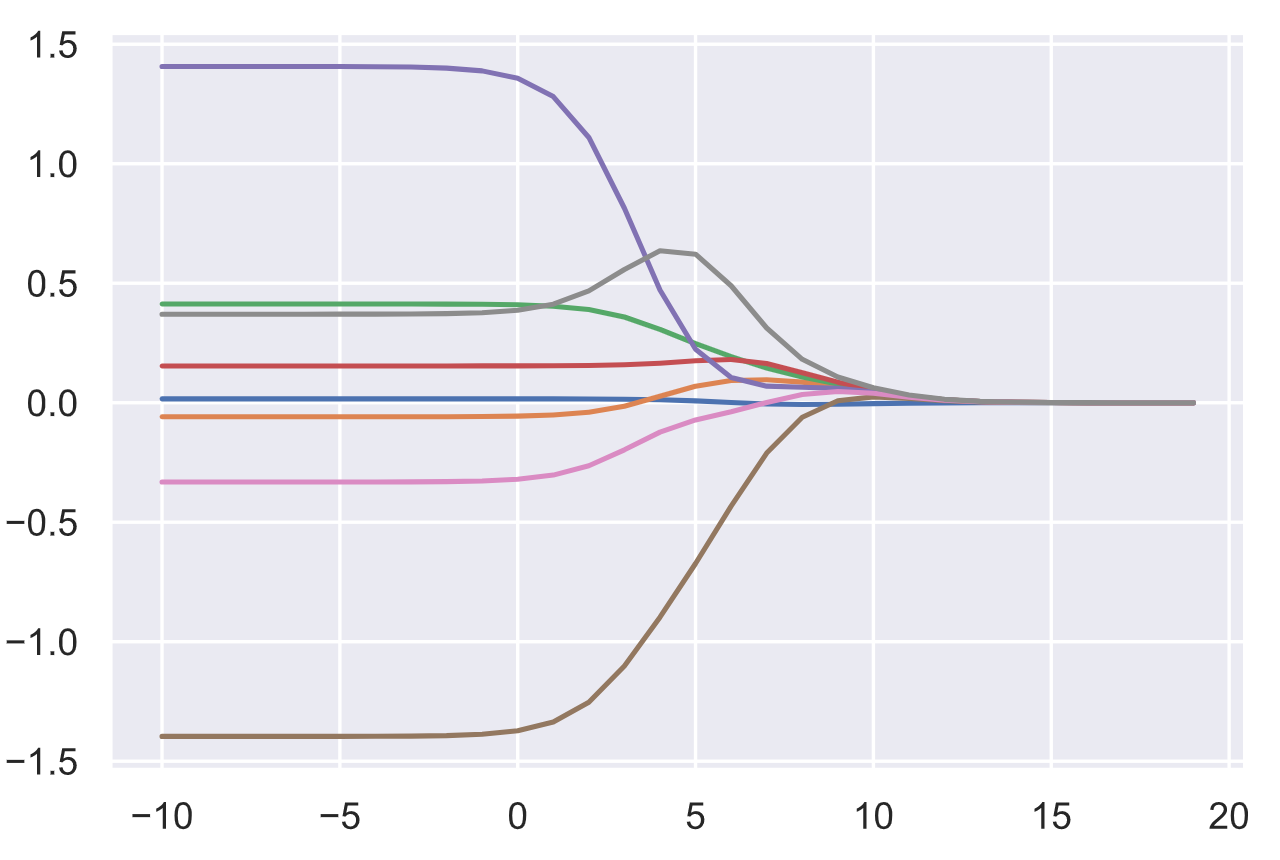
1. 当岭参数 $\lambda=0$ 时, 得到的解是最小二乘解.
2. 当岭参数 $\lambda$ 趋向更大时, 岭回归系数 $w_i$ 向于0.

4.1 Code

数据集: http://archive.ics.uci.edu/ml/datasets/Abalone

import numpy as np
import matplotlib.pyplot as plt

def load_data(filename):
    """
    加载数据
    """
    X, Y = [], []
    with open(filename, 'r') as f:
        for line in f:
            splited_line = [float(i) for i in line.split()]
            x, y = splited_line[: -1], splited_line[-1]
            X.append(x)
            Y.append(y)
    X, Y = np.matrix(X), np.matrix(Y).T
    return X, Y

def get_corrcoef(X, Y):
    """
    X Y 的协方差
    """ 
    cov = np.mean(X*Y) - np.mean(X)*np.mean(Y)
    return cov/(np.var(X)*np.var(Y))**0.5

def standarize(X):
    ''' 中心化 & 标准化数据 (零均值, 单位标准差)
    '''
    std_deviation = np.std(X, 0)
    mean = np.mean(X, 0)
    return (X - mean)/std_deviation

def ridge_regression(X, y, lambd=0.2):
    ''' 获取岭回归系数
    '''
    XTX = X.T*X
    m, _ = XTX.shape
    I = np.matrix(np.eye(m))
    w = (XTX + lambd*I).I*X.T*y
    return w

def ridge_traj(X, y, ntest=30):
    ''' 获取岭轨迹矩阵
    '''
    _, n = X.shape
    ws = np.zeros((ntest, n))
    for i in range(ntest):
        w = ridge_regression(X, y, lambd=np.exp(i-10))
        ws[i, :] = w.T
    return ws

if '__main__' == __name__:
    ntest = 30
    # 加载数据
    X, y = load_data('abalone.txt')

    # 中心化 & 标准化
    X, y = standarize(X), standarize(y)

    # 测试数据和训练数据
    w_test, errors = [], []
    for i in range(ntest):
        lambd = np.exp(i - 10)
        # 训练数据
        X_train, y_train = X[: 180, :], y[: 180, :]
        # 测试数据
        X_test, y_test = X[180: -1, :], y[180: -1, :]

        # 岭回归系数
        w = ridge_regression(X_train, y_train, lambd)
        error = np.std(X_test*w - y_test)
        w_test.append(w)
        errors.append(error)

    # 选择误差最小的回归系数
    w_best, e_best = min(zip(w_test, errors), key=lambda x: x[1])
    print('Best w: {}, best error: {}'.format(w_best, e_best))

    y_prime = X*w_best
    # 计算相关系数
    corrcoef = get_corrcoef(np.array(y.reshape(1, -1)),
                            np.array(y_prime.reshape(1, -1)))
    print('Correlation coefficient: {}'.format(corrcoef))

    # 绘制岭轨迹
    ws = ridge_traj(X, y, ntest)
    fig = plt.figure()
    ax = fig.add_subplot(111)

    lambdas = [i-10 for i in range(ntest)]
    ax.plot(lambdas, ws)

    plt.show()

岭轨迹图: 不同 $\lambda$ 下各特征回归系数的变化情况.

5. LASSO

LASSO(The Least Absolute Shrinkage and Selection Operator)是另一种缩减方法, 将回归系数收缩在一定的区域内. LASSO的主要思想是构造一个一阶惩罚函数获得一个精炼的模型, 通过最终确定一些变量的系数为0进行特征筛选.

LASSO的惩罚项为:

$$\sum_{i=1}^n|w_i|\le t$$

与岭回归的不同在于, 此约束条件使用了绝对值的一阶惩罚函数代替了平方和的二阶函数. 虽然只是形式稍有不同, 但是得到的结果却又很大差别. 在LASSO中, 当 $\lambda$ 很大的时候，一些系数会随着变为0, 而岭回归却很难使得某个系数恰好缩减为0. 具体的几何解释可以查看我的另一篇讲正则化的博文.