1. Logistic Regression
我们之前学习了如何使用线性模型进行回归学习. 但其实我们能使用最后所讲的广义线性模型我们能进行分类任务学习: 我们只需要找一个单调可微函数将分类任务的真实标记 $y$ 与线性回归模型的预测值联系起来.
我们从简单的二分类任务入门, 其输出标记 $y\in \{0,1\}$, 而线性回归模型产生的预测值 $z=w^Tx+b$ 是实值, 于是, 我们需要将实值 $z$ 转换为 0/1 值. 最理想的是单位阶跃函数 (unit-step function).
若预测值 $z$ 大于零就判为正例, 小于零则判为反例, 预测值为临界值零则可以任意判别. 我们不难发现单位阶跃函数存在一个问题, 就是不连续! 因此不能将单位阶跃函数用于广义线性模型. 因此我们可以用一个替代函数, 也就是下图中的对数几率函数(或者称为逻辑斯谛函数).
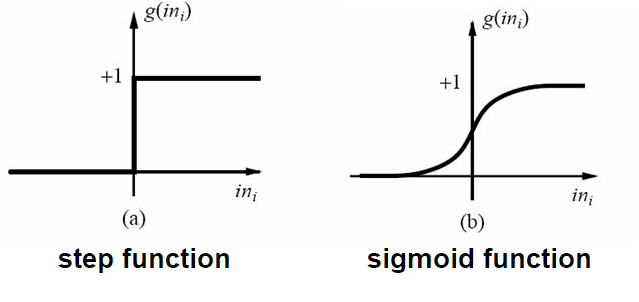
对数几率函数将 $z$ 值转换为一个接近 0 或 1 的 $y$ 值, 并且其输出值在 $z=0$ 附近变化很陡. 我们将对数几率函数代入广义线性模型之后, 可以得到
通过简单的数学变形, 我们可以得到下式
若将 $y$ 视为样本 $x$ 作为正例的可能性, 则 $1-y$ 是其反例的可能性, 两者的比值 $\frac{y}{1-y}$ 称为几率, 反映了 $x$ 作为正例的相对可能性. 对几率取对数则得到对数几率 (log odds, 亦称为 logit), $\log{\frac{y}{1-y}}$.
由此我们知道, $y=\frac{1}{1+\exp(-w^Tx-b)}$ 实际上是在用线性回归模型 ($z=w^Tx+b$) 的预测结果去逼近真实标记的对数几率 ($\log{\frac{y}{1-y}}$). 因此, 其对应的模型称为对数几率回归 (Logistic Regression, 或者叫做逻辑回归, 或逻辑斯谛回归). 需要注意的是, 虽然其名字里面有一个回归, 但其实际上是一种分类学习算法.
- 优点
- 模型: 模型清晰, 背后的概率推导经得住推敲.
- 输出: 输出值自然地落在0到1之间, 并且有概率意义.
- 参数: 参数代表每个特征对输出的影响, 可解释性强.
- 简单高效: 实施简单, 非常高效(计算量小、存储占用低), 可以在大数据场景中使用.
- 可扩展: 可以使用online learning的方式更新轻松更新参数, 不需要重新训练整个模型.
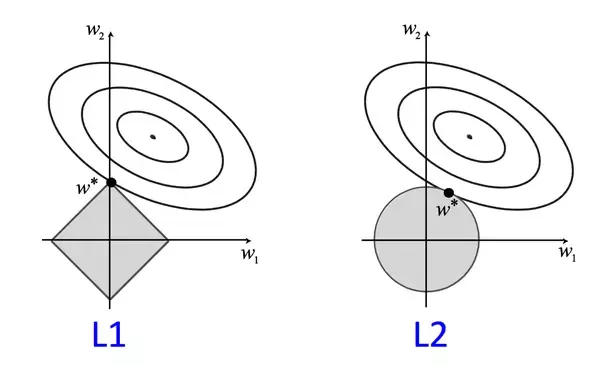
- 过拟合: 解决过拟合的方法很多, 如L1、L2正则化.
- 多重共线性: L2正则化就可以解决多重共线性问题.
缺点
- 特征相关情况: 因为它本质上是一个线性的分类器, 所以处理不好特征之间相关的情况.
- 特征空间: 特征空间很大时, 性能不好.
- 精度: 容易欠拟合, 精度不高.
使用注意事项
- 建模数据量不能太少
- 排除自变量中共线性的问题
- 异常值会给模型带来很大的干扰
我们在使用逻辑回归的时候很少会把数据直接丢给 LR 来训练, 我们一般会对特征进行离散化处理, 这样做的优势大致有以下几点:
- 离散后稀疏向量内积乘法运算速度更快, 计算结果也方便存储, 容易扩展;
- 离散后的特征对异常值更具鲁棒性, 如 age>30 为 1 否则为 0, 对于年龄为 200 的也不会对模型造成很大的干扰;
- LR 属于广义线性模型, 表达能力有限, 经过离散化后, 每个变量有单独的权重, 这相当于引入了非线性, 能够提升模型的表达能力, 加大拟合;
- 离散后特征可以进行特征交叉, 提升表达能力, 由 M+N 个变量编程 M*N 个变量, 进一步引入非线形, 提升了表达能力;
- 特征离散后模型更稳定, 如用户年龄区间, 不会因为用户年龄长了一岁就变化;
1.1 Decision Boundary
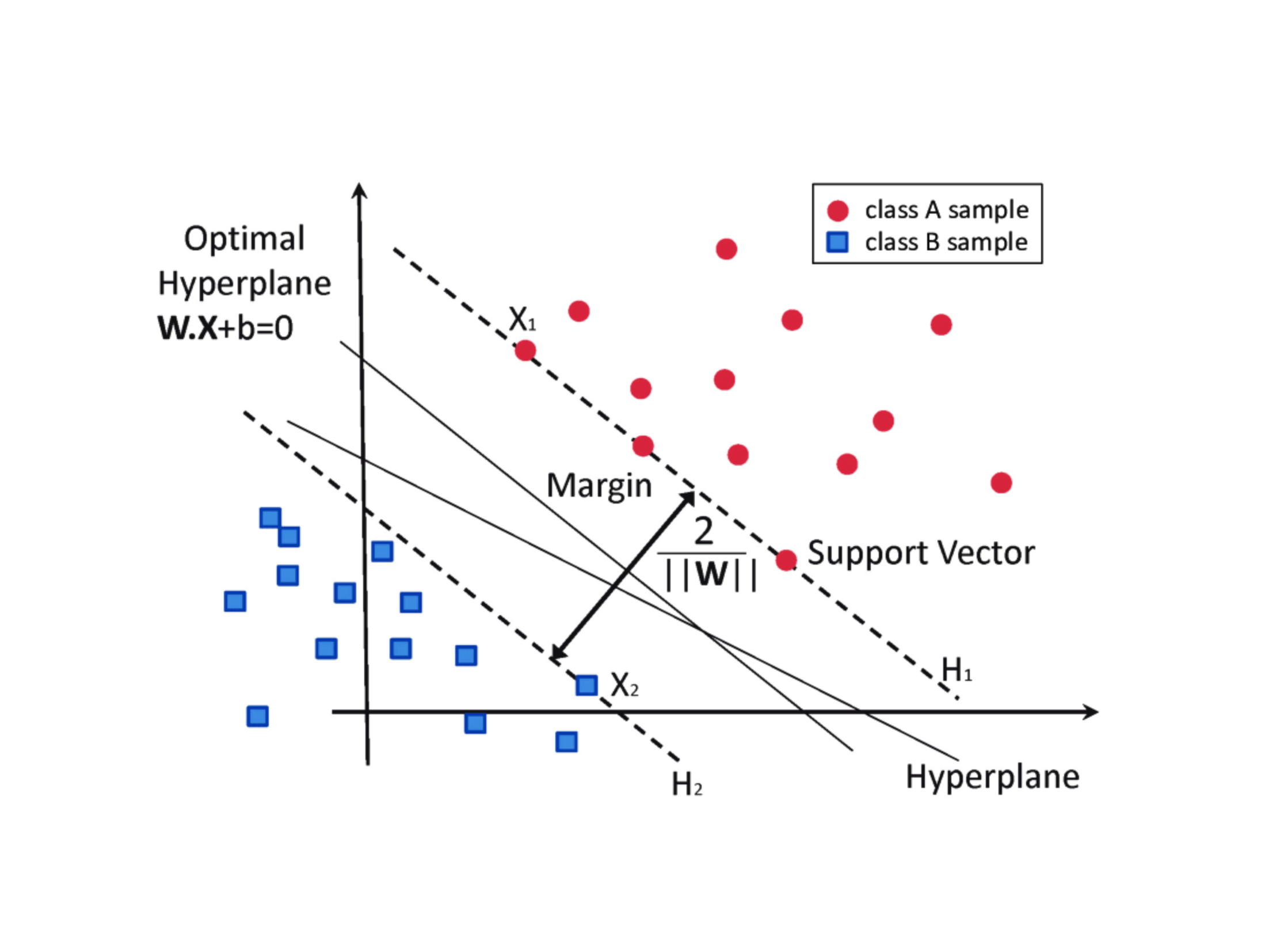
根据上面的对数几率公式: $\log\frac{y}{1-y}=w^Tx+b$, 我们很容易知道, 逻辑回归的决策边界为 $w^Tx+b=0$. 根据样本 $x$ 的维度不同, 该决策边界可以是一条直线或者是一个超平面.
我们用鸢尾花数据集来可视化一下决策边界. 我们首先可视化数据集:
1 | import numpy as np |
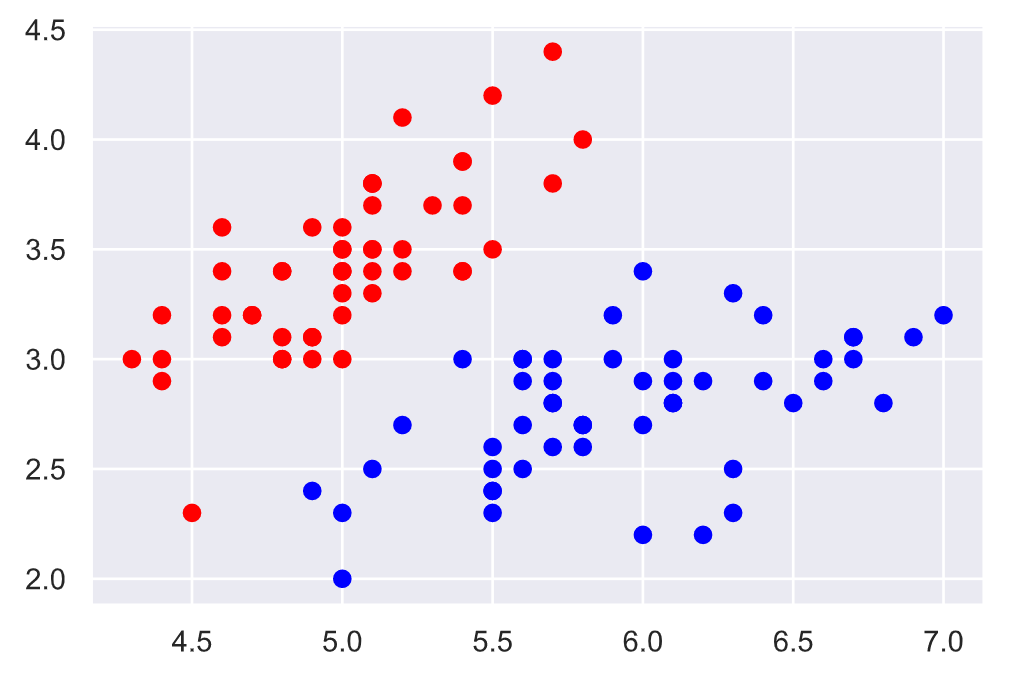
然后使用逻辑回归进行训练:
1 | from sklearn.model_selection import train_test_split |
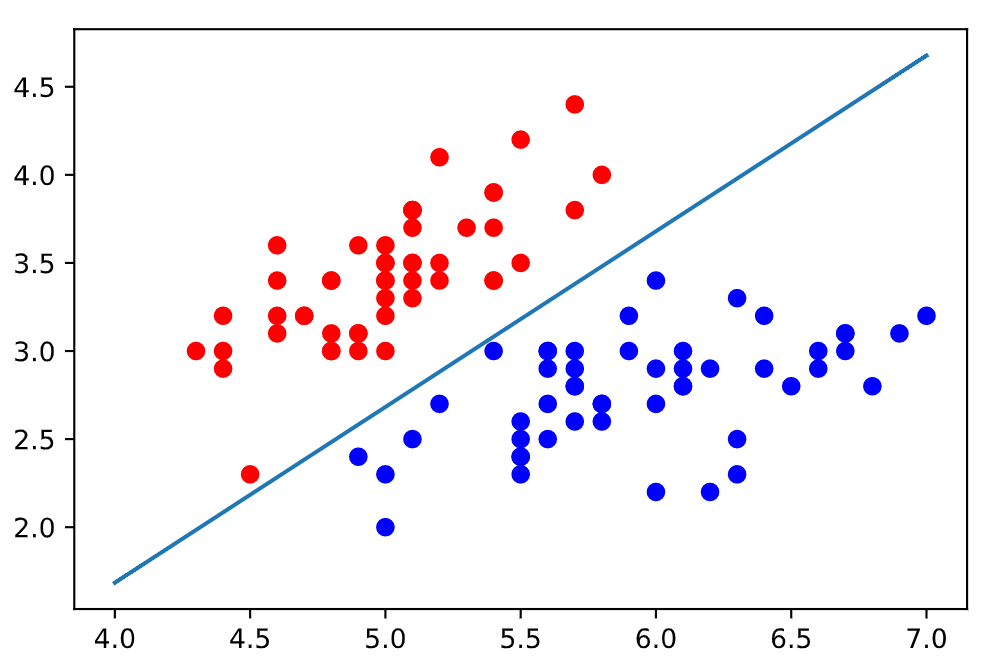
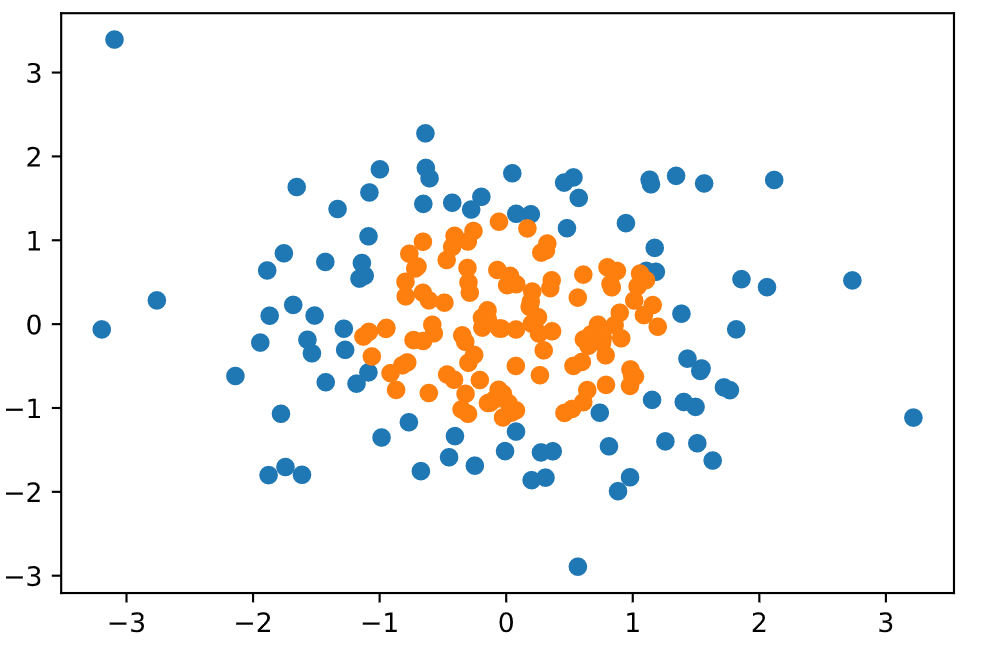
但其实决策边界也可以是非线性的, 如果我们遇到下图的情况, 我们就不能用一个直线将其分类了, 而是可以用一个类似圆的图形将数据进行分类.
1 | import numpy as np |
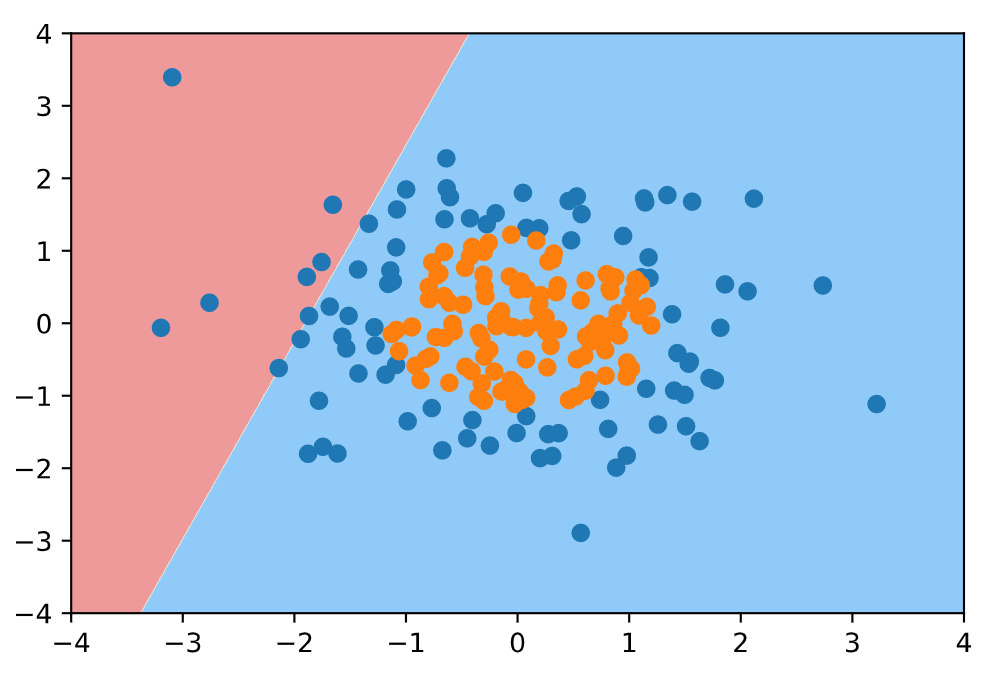
首先我们使用没添加多项式项的逻辑回归函数, 对上面的样本进行划分. 得到的分类结果应该是很差的.
1 | from sklearn.linear_model import LogisticRegression |
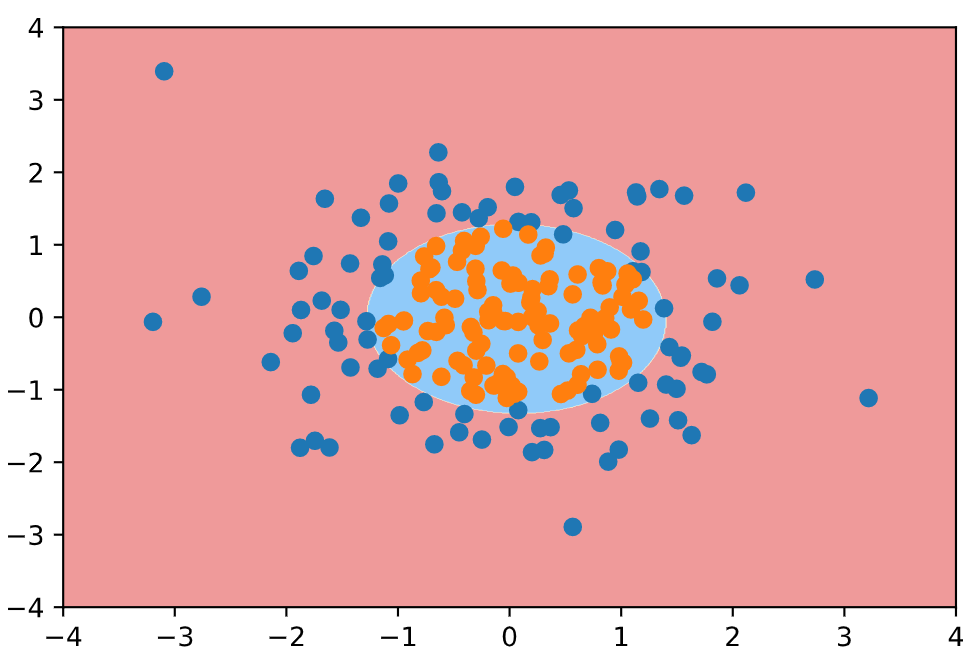
然后使用逻辑回归的方式添加多项式特征, 对上面的样本进行划分: 为逻辑回归算法添加多项式项, 设置pipeline. 管道的第一步是添加多项式项, 第二部是归一化, 第三部进行逻辑回归过程, 返回实例对象.
1 | from sklearn.preprocessing import PolynomialFeatures |
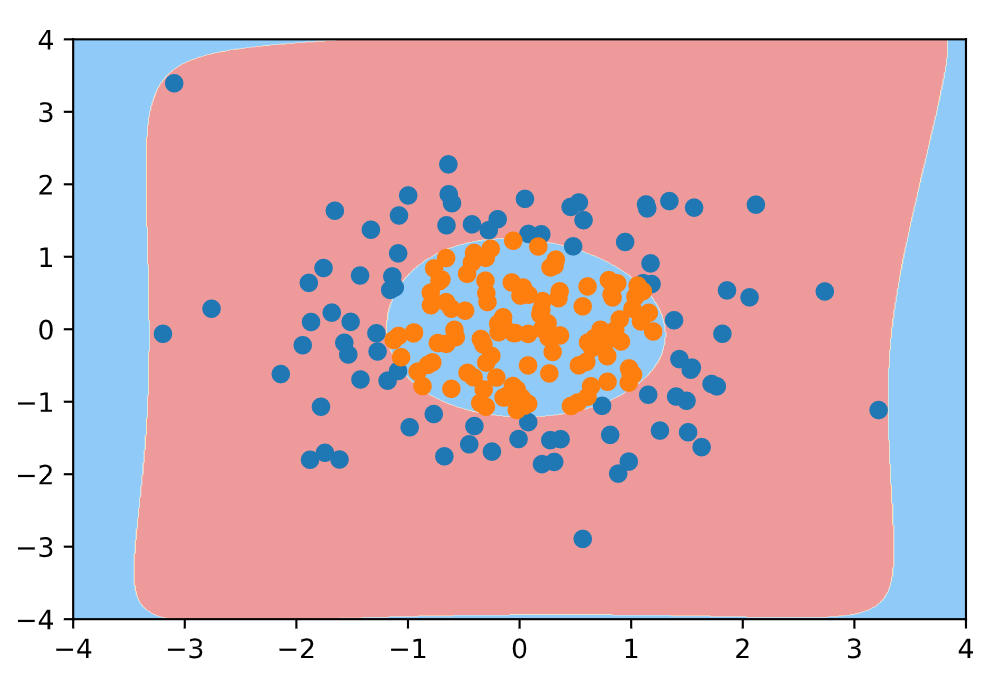
下面我们更改degree参数 (多项式拓展的阶数), 将其变大 (那肯定会过拟合):
1 | poly_log_reg2 = PolynomialLogisticRegression(degree=20) |
我们可以在创建 clf 的时候, 可以使用 penalty 参数来防止过拟合.
1.2 Parameter Estimation
现在我们来研究如何求解参数 $w$ 和 $b$. 我们若将 $y$ 视作类后验概率估计 $P(y=1|x)$, 则对数几率 $\log{\frac{y}{1-y}}$ 可以重写为
显然有
于是, 我们可通过极大似然法 (maximum likelihood method) 来估计 $w$ 和 $b$. 给定数据集 $\{(x_i,y_i)\}_{i=1}^N$, $y_i\in\{0,1\}$, 对数几率回归模型最大化对数似然 (log likelihood).
设:
似然函数 (Likelihood Function) 为
对数似然函数 (Log Likelihood Function) 为
通过对 $L(w,b)$ 求极大值, 我们得到 $w,b$ 的估计值. (如果还记得Cross Entropy, 那么极大化对数似然函数就是在最小化Cross Entropy Error) 常用的方法是梯度下降法和牛顿法.
3. Multinomial Logistic Regression
多元逻辑回归也被称为 Softmax Regression 或 Multiclass Logistic Regression.
我们拥有的数据集如下:
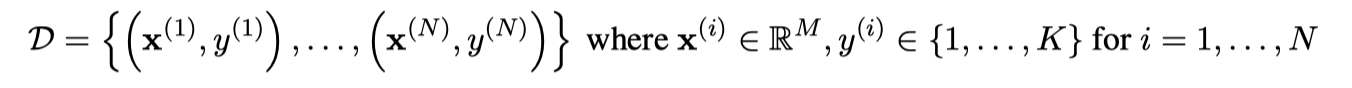
- N 是样本数
- K 是类别数
- M 是特征数
我们的分类器如下:
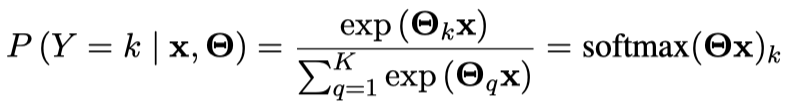
- $\Theta$ 是 $K\times(M+1)$ 的矩阵
- $\Theta_k$ 是矩阵 $\Theta$ 的第 $k$ 行, 代表 k-th class 的参数向量
- 我们假设我们往矩阵 $\Theta$ 增加了 bias 列, 因此 $x^{(i)}\in\mathbb{R}^{M+1}$
因此对于单个训练样本, 其似然为:
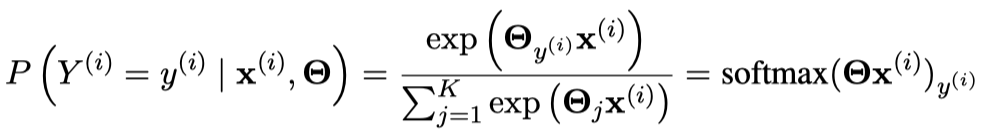
同时我们假设 $Y^{(i)}$ 是独立同分布的, 因此我们能将数据集最大似然估计表示为:
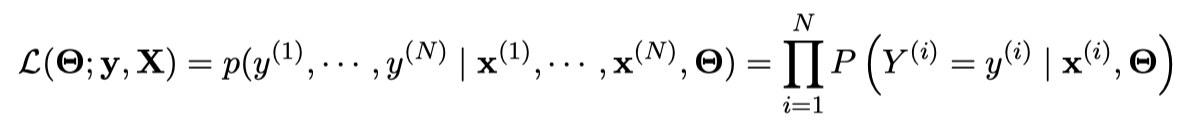
我们新建一个大小为 $N\times K$ 的矩阵 $\mathbf{T}$, 其中 $\mathbf{T}_{ij}=\mathbb{I}(y^{(i)}=j)$. 因此上式可以表示为:
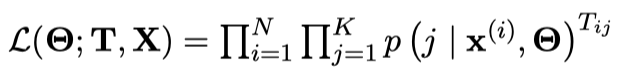
进而我们的损失函数可以表示为:
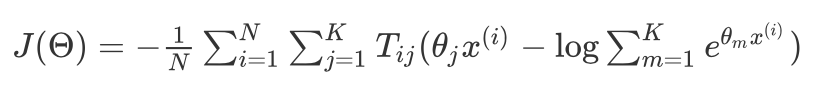
那么我们对 $J(\Theta)$ 求偏导可以得到:
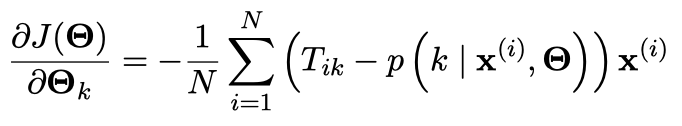
4. Implementation
项目地址: https://github.com/alvisdeng/NLP-Sentiment-Polarity-Analyzer