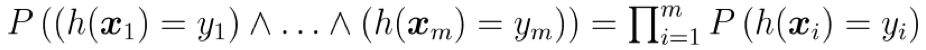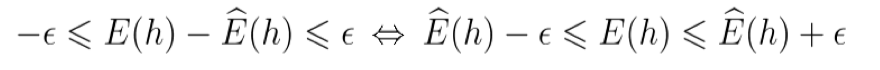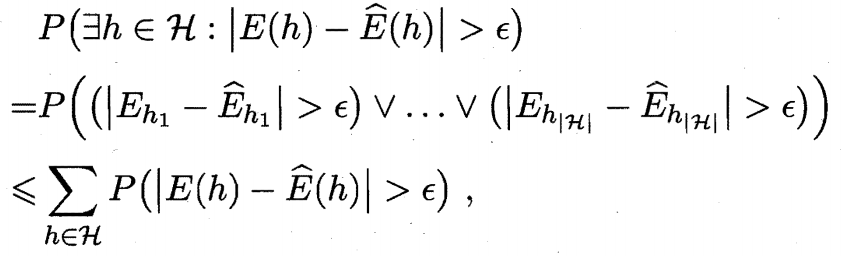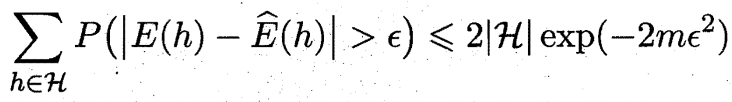1. Entree
统计学中由总体集合和样本集合之分, 比如要统计国内本科生对机器学习的掌握情况, 此时全国所有的本科生就是总体集合, 但总体集合往往太大而不具有实际可操作性, 一般都是取总体集合的一部分, 也就是样本集合.
在机器学习中, 样本空间对应总体集合, 而我们手头上的样例集 $D$ 对应样本集合, 样例集 $D$ 是从样本空间中采样而得, 分布 $\mathcal{D}$ 可理解为当从样本空间采样获得样例集 $D$ 时每个样本被采到的概率. 我们用 $\mathcal{D}(t)$ 表示样本空间第 $t$ 个样本被采到的概率.
给定样例集 $D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)\}$, 其中 $\boldsymbol{x}_i\in\mathcal{X},y_i\in\mathcal{Y}=\{-1,+1\}$. 我们假设 $\mathcal{X}$ 中的所有样本服从一个隐含未知的分布 $\mathcal{D}$, $D$ 中所有样本都是独立地从这个分布上采样而得, 即独立同分布样本.
我们令 h 为 $\mathcal{X}$ 到 $\mathcal{Y}$ 的一个映射, 所以泛化误差可以表示为
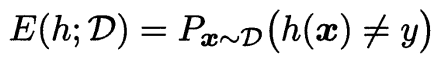
$P_{\boldsymbol{x}\sim D}(h(\boldsymbol{x})\neq y)$ 表示从样本空间中按分布 $\mathcal{D}$ 取一个样本 $\boldsymbol{x}$, 预测的类别标记不等于真实类表标记的概率, 即泛化误差.
在接下来的分析中, 我们有时会省略 $\boldsymbol{x}\sim\mathcal{D}$. 同时, 我们会将 $E(h;\mathcal{D})$ 简记为 $E(h)$.
泛化误差是 $h$ 在分布 $\mathcal{D}$ 上的期望误差.
$h$ 在 $D$ 上的经验误差为
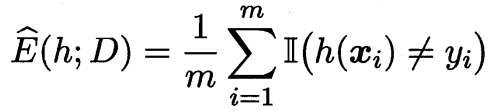
即是在训练集上的误差. 我们会将 $\hat{E}(h;D)$ 简写为 $\hat{E}(h)$.
经验误差是 $h$ 在训练集 $D$ 上的平均误差.
若 $h$ 在数据集 $D$ 上的经验误差为 0, 则称 $h$ 与 $D$ 一致, 否则称其与 $D$ 不一致. 对任意两个映射 $h_1,h_2\in\mathcal{X}→\mathcal{Y}$, 可通过其不合(disagreement)来度量它们之间的差别:
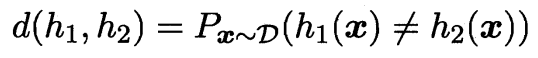
几个常用的不等式:
Jensen 不等式
对于任何凸函数 $f(x)$, 有
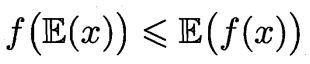
我们简单介绍一下凸凹函数
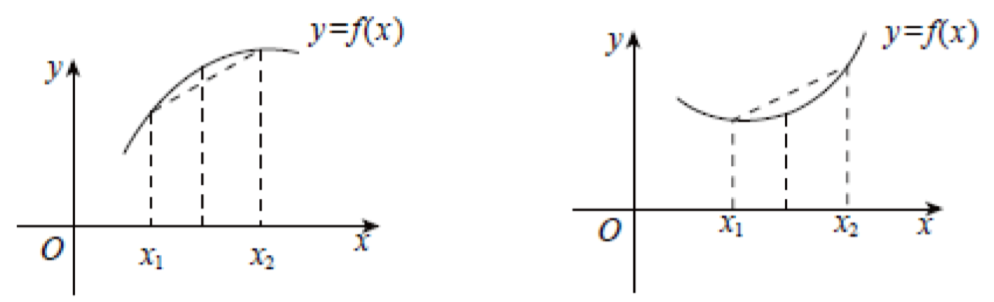
左为凹函数: 满足 $f(\frac{x_1+x_2}{2})\gt\frac{f(x_1)+f(x_2)}{2}$;
右为凸函数: 满足 $f(\frac{x_1+x_2}{2})\lt\frac{f(x_1)+f(x_2)}{2}$;
Hoeffding 不等式
若 $x_1,x_2,…,x_m$ 为 $m$ 个独立随机变量, 且满足 $0\le x_i\le1$, 则对任意 $\epsilon>0$, 有
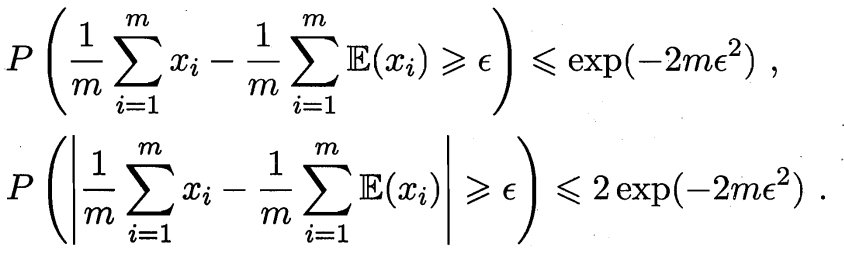
式中, $\frac{1}{m}\sum_{i=1}^mx_i$ 表示 $m$ 个独立随机变量各种的某次观测值的平均值. $\frac{1}{m}\sum_{i=1}^m\mathbb{E}(x_i)$ 表示 $m$ 个独立随机变量各自的期望的平均.
第一个不等式表示事件 $\frac{1}{m}\sum_{i=1}^mx_i-\frac{1}{m}\sum_{i=1}^m\mathbb{E}(x_i)\ge\epsilon$ 出现概率不大于 $e^{-2m\epsilon^2}$, 第二个等式同理.
Hoeffding 不等式给出了随机变量和与其期望值偏差的概率上限.
McDiarmid 不等式
若 $x_1,x_2,…,x_m$ 为 $m$ 个独立随机变量, 且对任意 $1\le i\le m$, 函数 $f$ 满足
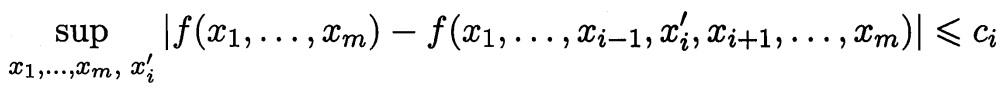
则对任意 $\epsilon>0$, 有
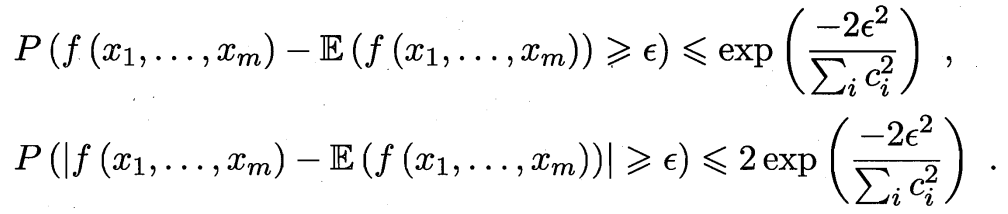
首先, 函数 $f$ 有 $m$ 个输入变量, 相比于 $f(x_1,…,x_m)$, $f(x_1,…,x_{i-1},x_i’,x_{i+1},…,x_m)$ 将第 $i$ 个输出由 $x_i$ 改为 $x_i’$. 所以 $|f(x_1,…,x_m)-f(x_1,…,x_{i-1},x_i’,x_{i+1},…,x_m)|$ 表示改变第 $i$ 个输入后函数值发生的变化量. sup 表示上确界 (supremum).
$x_1,x_2,…,x_m$ 为 $m$ 个独立随机变量, $f(x_1,…,x_m)$ 表示某次观测时对应的函数值. 每次观测中, 随机变量的取值不同则对应的函数值也不同.
2. PAC Learning Theory
我们希望用 PAC 理论在解释以下几个问题:
- 什么样的问题能够被有效率的学习 (What can be learned efficiently)?
- 什么样的问题天生无法有效地被学习 (What is inherently hard to learn)?
- 成功的学习需要多少样本 (How many examples are needed to learn successfully)?
- 学习有没有一个综合性的模型指导 (Is there a general model of learning)?
计算学习理论中最基本的是 概率近似正确 (Probably Approximately Correct, 简称 PAC) 学习理论. 我们首先介绍两个基本概念:
概念类 (Concept Class)
我们令 $c$ 表示概念 (concept), 这是从样本空间 $\mathcal{X}$ 到标记空间 $\mathcal{Y}$ 的映射, 它决定样例 $\boldsymbol{x}$ 的真实标记 $y$, 若对任何样例 $(\boldsymbol{x},y)$ 有 $c(\boldsymbol{x})=y$ 成立, 则称 c 为目标概念, 所有目标概念所构成的集合称为概念类 (concept class), 用符号 $\mathcal{C}$ 表示.
即 c 表示能够准确预测所有样本(不仅限于训练集或测试集)的模型.
假设空间 (Hypothesis Space)
给定学习算法 $\mathfrak{L}$, 它所考虑的所有可能概念的集合称为假设空间 (Hypothesis Space), 用符号 $\mathcal{H}$ 表示.
若目标概念 $c\in\mathcal{H}$, 则 $\mathcal{H}$ 中存在假设能将所有示例按与真实标记一致的方式完全分开, 我们称该问题对学习算法是 可分的 (Separable), 也可以叫做一致的 (Consistent). 或者按照我们课程上所说是 Realizable 的.
若目标概念 $c\notin\mathcal{H}$ or $c\in\mathcal{H}$, 则 $\mathcal{H}$ 中可能存在假设能将所有示例按与真实标记一致的方式完全分开, 我们则称该学习算法是 Agnostic 的.
若目标概念 $c\notin\mathcal{H}$, 则 $\mathcal{H}$ 中不存在假设能将所有示例按与真实标记一致的方式完全分开, 我们则称该学习算法是不一致的 (Inconsistent) 的.
为什么是 PAC, 或者说叫做概率近似正确?
在机器学习中, 是给定训练集, 我们基于学习算法学得的模型所对应的假设 $h$ 应该尽可能接近目标概念 $c$. 这是因为机器学习过程往往受到很多因素的制约, 比如:
- 训练集仅含有限数量的样例
- 从分布 $\mathcal{D}$ 采样得到 $D$ 的过程有一定的偶然性
现在我们来看看一些和 PAC 相关的定义, 我们令 $\delta$ 表示置信度:
==定义 1: PAC 辨识 (PAC Identify)==
对 $0<\epsilon,\delta<1$, 所有 $c\in\mathcal{C}$ 和分布 $\mathcal{D}$, 若存在学习算法 $\mathfrak{L}$, 其输出假设 $h\in\mathcal{H}$ 能满足
我们则称学习算法 $\mathfrak{L}$ 能从假设空间 $\mathcal{H}$ 中 PAC 辨识概念类 $\mathcal{C}$.
换句通俗一点的话说就是: 输出假设 $h$ 的泛化误差 $E(h)\le\epsilon$ 的概率不小于 $1-\delta$.
再换一句更通俗的话说就是: 学习算法 $\mathfrak{L}$ 能以较大概率 (至少$1-\delta$) 学得目标概念 $c$ 的近似 (误差最大为 $\epsilon$).
==定义 1.1: PAC Criterion==
接下来我们介绍一个在 10-601 上学到的类似概念
The PAC criterion is that our learner produces a high accuracy learner with high probability:
==定义 2: PAC 可学习 (PAC Learnable)==
令 $m$ 表示从分布 $\mathcal{D}$ 中独立同分布采样得到的样例数目, $0<\epsilon,\delta<1$, 对所有分布 $\mathcal{D}$, 若存在学习算法 $\mathfrak{L}$ 和多项式函数 $poly(·,·,·,·)$, 使得对于任何 $m\ge poly(\frac{1}{\epsilon},\frac{1}{\delta},size(\boldsymbol{x}),size(c))$, 学习算法 $\mathfrak{L}$, 能从假设空间 $\mathcal{H}$ 中 PAC 辨识 概念类 $\mathcal{C}$, 我们则称概念类 $\mathcal{C}$ 对假设空间 $\mathcal{H}$ 而言是 PAC 可学习的.
$\epsilon$: 误差
$\delta$: 置信度
$size(\boldsymbol{x})$: 数据本身的复杂度
$size(c)$: 目标概念的复杂度
因此, 我们知道, 一个概念类 $\mathcal{C}$ 被称为 PAC 可学习的则意味着: 算法在观测完一定数量 (数量是 $\frac{1}{\epsilon},\frac{1}{\delta},size(\boldsymbol{x}),size(c)$ 的多项式函数) 的样本后, 所返回的假设, 在很大程度上 (至少为 $1-\delta$) 是近似正确的 (approximately right, 错误最多为 $\epsilon$).
==定义 3: PAC 学习算法 (PAC Learning Algorithm)==
若学习算法 $\mathfrak{L}$ 使概念类 $\mathcal{C}$ 为 PAC 可学习的, 且算法 $\mathfrak{L}$ 的运行时间也是多项式函数 $poly(\frac{1}{\epsilon},\frac{1}{\delta},size(\boldsymbol{x}),size(c))$, 我们则称概念类 $\mathcal{C}$ 是高效 PAC 可学习的, 且学习算法是 $\mathfrak{L}$ 是概念类 $\mathcal{C}$ 的 PAC 学习算法.
==定义 4: PAC 样本复杂度 (Sample Complexity)==
满足 PAC 学习算法 $\mathfrak{L}$ 所需的 $m\ge poly(\frac{1}{\epsilon},\frac{1}{\delta},size(\boldsymbol{x}),size(c))$ 中最小的 $m$, 称为学习算法 $\mathfrak{L}$ 的样本复杂度.
有了上述定义之后我们抛出来三个问题:
- 研究某任务在什么样的条件下可学得较好的模型? 定义 2
- 某算法在什么样的条件下可进行有效的学习? 定义 3
- 需要多少训练样例才能获得较好的模型? 定义 4
PAC 的要点:
- PAC框架对分布 $\mathcal{D}$ 没有任何假设, 仅假设其存在.
- 训练样本和测试样本都是从同一分布中产生的.
- PAC可学习是针对概念类谈的, 而非特定的那个目标概念.
3. Hypothesis Space
有限假设空间指 $\mathcal{H}$ 中包含的假设个数是有限的, 反之则为无限假设空间. 无限假设空间更为常见. 一般而言, $\mathcal{H}$ 越大, 其包含任意目标概念的可能性越大, 但从中找到某个具体目标概念的难度也越大.
我们之前已经了解过了学习算法 consistent, inconsistent, agnostic 的概念. 我们现在想知道在不同的情形下我们要达成 PAC 可学习的样本数量. 在这里我们先给出结论:

3.1 Finite and Realizable
Realizable(Consistent) 意味着目标概念 $c$ 属于假设空间 $\mathcal{H}$. 给定包含 $m$ 个样本的训练集 $D$, 如何找出满足误差参数的假设呢?
记住! 我们要做的并不是找到 $c$, 而是要找到 $c$ 的近似! (即是训练误差为 0)
==我们先估计泛化误差大于 $\epsilon$ 但在训练集仍然表现完美的假设出现的概率 (我们要令这个概率小于某个值, 因为我们其实是希望泛化误差小于 $\epsilon$ 但经验误差为零的假设出现的概率不小于 $1-\delta$)==. 假定 $h$ 的泛化误差大于 $\epsilon$, 对分布 $\mathcal{D}$ 上随机采样而得的任何样例 $(\boldsymbol{x},y)$, 有
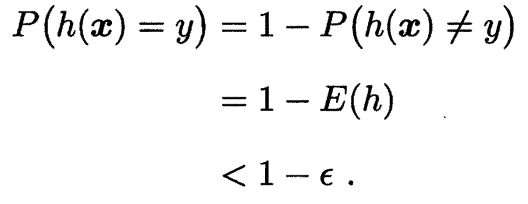
第 1 个等号是由于 $P(h(\boldsymbol{x}=y)+P(h(\boldsymbol{x}\neq y)=1$ 恒成立;
第 2 个等号是由于 $P(h(\boldsymbol{x}\neq y)$ 就是泛化误差;
第 3 个等号是由于我们之前假设泛化误差 $E(h)>\epsilon$, 因此 $1-E(h)<1-\epsilon$
由于 $D$ 包含 $m$ 个从 $\mathcal{D}$ 独立同分布采样而得的样例, 因此, $h$ 与 $D$ 表现一致 (经验误差为 0) 的概率为
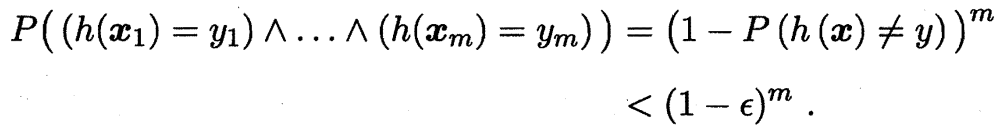
由于 $D$ 包含的 $m$ 个样例是从 $\mathcal{D}$ 独立同分布采样而得, 因此
其中, $\and$ 表示逻辑与, $\prod$ 表示连乘; 上述推导使用了概率论中的结论: 若事件 $A$ 和事件 $B$ 独立, 则 $P(AB)=P(A)P(B)$
我们事先并不知道学习算法 $\mathfrak{L}$ 会输出 $\mathcal{H}$ 中的哪个假设, ==但我们仅需保证泛化误差大于 $\epsilon$, 且在训练集上表现完美的所有假设出现概率之和不大于 $\delta$ 即可==
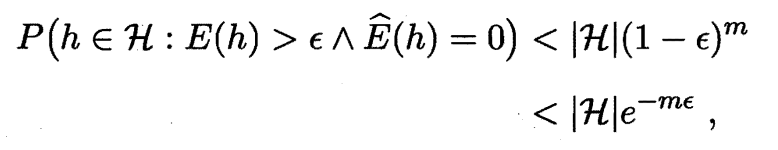
令上式不大于 $\delta$, 即
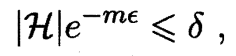
可得 Sample Complexity
同时我们也能得到 Error Bound
因此用泛化边界的思路可以阐述为
==在这里, 经验误差 $\hat{E}(h)=0$, 做的事情是以 $1-\delta$ 概率学得目标概念的 $\epsilon$ 近似. 因此, 我们知道有限假设空间 $\mathcal{H}$ 都是 PAC 可学习的, 所需样例数目: $m\ge\frac{1}{\epsilon}(\ln|\mathcal{H}|+\ln\frac{1}{\delta})$.==
① 概率 $P(h\in\mathcal{H}:E(h)>\epsilon\and\hat{E}(h)=0)$ 表示: 对于假设空间 $\mathcal{H}$ 中某个特定假设 $h$, 事件 $E(h)>\epsilon$ 和事件 $\hat{E}(h)=0$ 同时成立的概率.
② 根据之前的分析, 我们知道事件 $E(h)>\epsilon$ 和事件 $\hat{E}(h)=0$ 同时成立的概率 $P(E(h)>\epsilon\and\hat{E}(h)=0)<(1-\epsilon)^m$.
③ 假设空间 $\mathcal{H}$ 中共包含 $|\mathcal{H}|$ 个假设, 概率之和如下:
④ 这 $|\mathcal{H}|$ 个假设各自满足事件 $E(h)>\epsilon$ 和事件 $\hat{E}(h)=0$ 成立的概率均小于 $(1-\epsilon)^m$, 即对于 $\forall h_i\in\mathcal{H},P(E(h_i)>\epsilon\and\hat{E}(h_i)=0)<(1-\epsilon)^m$, 因此上式第一个小于号成立.
⑤ 因为 $|\mathcal{H}|$ 和 $m$ 均为正数, 因此第二个小于号实际要证明 $(1-\epsilon)<e^{-\epsilon}$.
⑥ 令函数 $f(\epsilon)=1-\epsilon-e^{-\epsilon}$, 其中定义域为泛化误差 $\epsilon\in[0,1]$; 对函数求导得到 $f’(\epsilon)=-1+e^{-\epsilon}$, 在定义域内, 导数小于等于 0 恒成立, 因此 $f(\epsilon)$ 是单调递减函数, 最大值是 $f(0)=0$, 因此 $(1-\epsilon)\le e^{-\epsilon}$.
3.2 Finite and Agnostic
对较为困难的学习问题, 目标概念 $c$ 往往不存在于假设空间中. 假定对于任何 $h\in\mathcal{H}$, $\hat{E}(h)\ne0$, 也就是说, $\mathcal{H}$ 中任意一个假设都会在训练集出现或多或少的错误.
==引理 1==
若训练集 $D$ 包含 $m$ 个从分布 $\mathcal{D}$ 上独立同分布采样而得的样例, $0<\epsilon<1$, 则对任意 $h\in\mathcal{H}$, 有
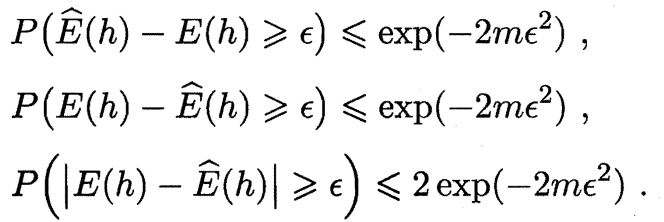
==推论 1==
若训练集 $D$ 包含 $m$ 个从分布 $\mathcal{D}$ 上独立同分布采样而得的样例, $0<\epsilon<1$, 则对任意 $h\in\mathcal{H}$, 下式以至少 $1-\delta$ 的概率成立
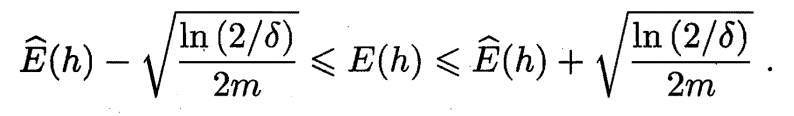
上述推论表明, 样例数目 $m$ 较大时, $h$ 的经验误差是其泛化误差很好的近似.
上述推论的推导过程:
我们令 $\delta=2e^{-2m\epsilon^2}$, 则 $\epsilon=\sqrt{\frac{\ln(\frac{2}{\delta})}{2m}}$. 因此, 引理 1 的第三式可以表示为 $P(|E(h)-\hat{E}(h)|\ge\epsilon)\le\delta$, 而这等价于 $P(|E(h)-\hat{E}(h)|\le\epsilon)\ge1-\delta$, 即 $|E(h)-\hat{E}(h)|\le\epsilon$ 成立的概率不小于 $1-\delta$.
对于不等式 $|E(h)-\hat{E}(h)|\le\epsilon$, 其等价于
最后将 $\delta=2e^{-2m\epsilon^2}$ 代入即可.
==定理 1==
若 $\mathcal{H}$ 为有限假设空间, $0<\delta<1$, 则对任意 $h\in\mathcal{H}$, 有
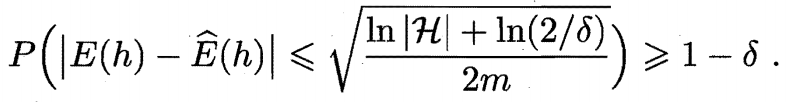
证明 令 $h_1,h_2,…,h_{|\mathcal{H}|}$ 表示假设空间 $\mathcal{H}$ 中的假设, 有
由引理 1 第三式可得
于是令 $\delta=2|\mathcal{H}|\exp(-2m\epsilon^2)$ 即可得定理 1.
显然, 当 $c\notin \mathcal{H}$ 时, 学习算法无法学得目标概念 $c$ 的 $\epsilon$ 近似 (因为经验误差无法做到 0). 但是根据上述分析, 我们知道当给定假设空间时, 其中必存在一个泛化误差最小的假设, 找出此假设的 $\epsilon$ 近似也不失为一个较好的目标.