1. M-P Neuron Model
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络, 它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应.
神经网络中最基本的成分是神经元 (Neuron)模型, 即上述定义中的”简单单元”. 在生物神经网络中, 每个神经元与其他神经元相连, 当它兴奋时, 就会向相连的神经元发送化学物质, 从而改变这些神经元内的电位; 如果某神经元的电位超过了一个阈值 (threshold), 那么它就会被激活, 即兴奋起来, 向其他神经元发送化学物质. 下图就是上述描述很好的抽象表示 $→$ M-P 神经元模型.
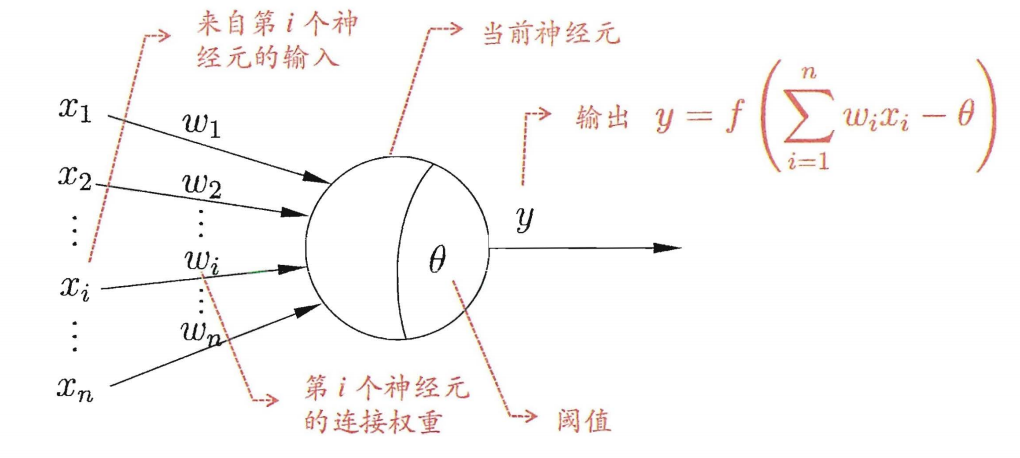
在这个模型中, 神经元接受到来自 $n$ 个其他神经元传递过来的输入信号, 这些输入信号通过带权重的连接进行传递, 神经元接收到的总输入值将与神经元的阈值进行比较, 然后通过激活函数 (activation function) 处理以产生神经元的输出.
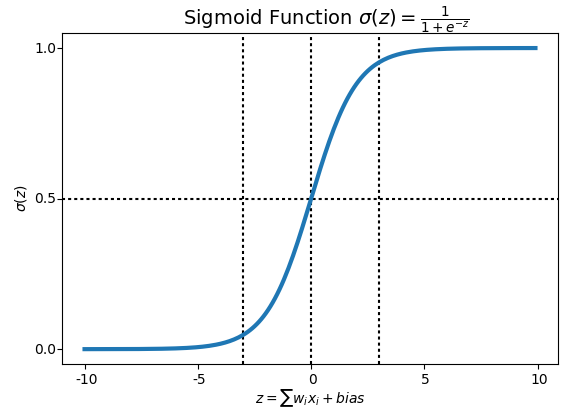
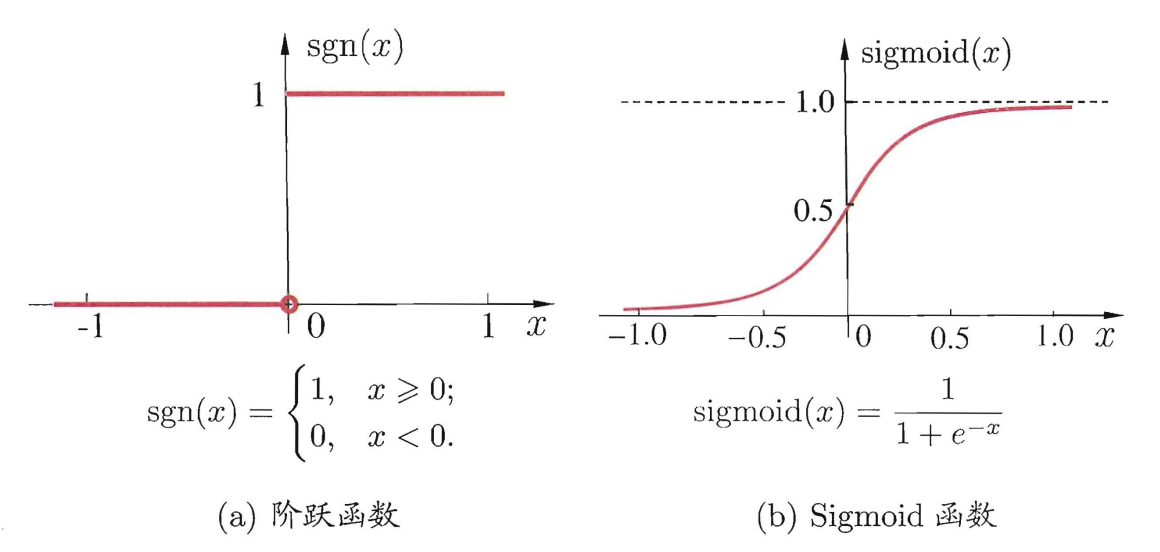
理想中的激活函数是图 (a) 所示的阶跃函数, 它将输入值映射为输出值 0 或 1. 0 对应神经元兴奋, 1 对应神经元抑制. 然而, 阶跃函数具有不连续, 不光滑等不友好的性质, 我们实际常用 Sigmoid 或者 ReLU 函数作为激活函数.
把许多个这样的神经元按一定的层次结构连接起来, 我们就得到了神经网络. 事实上, 从计算机科学的角度看, 我们可以不先考虑神经网络是否真的模拟了生物神经网络, 只需将一个神经网络视为包含了许多参数的数学模型, 这个模型是若干个函数.
2. Perceptron
感知机 (Perceptron) 由两层神经元组成, 输入层接收外界输入信号后传递给输出层, 输出层是 M-P 神经元.
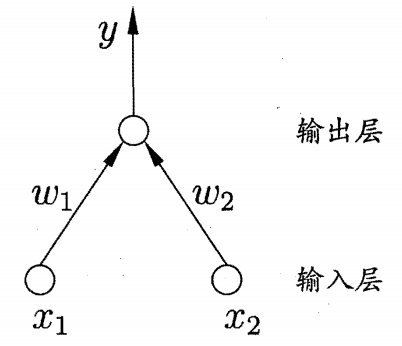
给定训练数据集, 权重 $w_i (i=1,2,…,n)$ 以及阈值 $\theta$ 可通过学习得到. 阈值 $\theta$ 可看作一个固定输入为 -1.0 的“哑结点” (dummy node) 所对应的连接权重 $w_{n+1}$, 这样, 权重和阈值的学习就可统一为权重的学习. 感知机学习规则非常简单, 对训练样例 ($\mathbf{x},y$), 若当前感知机的输出为 $\hat{y}$, 则感知机权重将这样调整:
其中 $\eta\in(0,1)$ 称为学习率 (learning rate). 从上式可看出, 若感知机对训练样例 ($\mathbf{x},y$) 预测正确, 即 $\hat{y}=y$, 则感知机不发生改变, 否则将根据错误的程度进行权重调整.
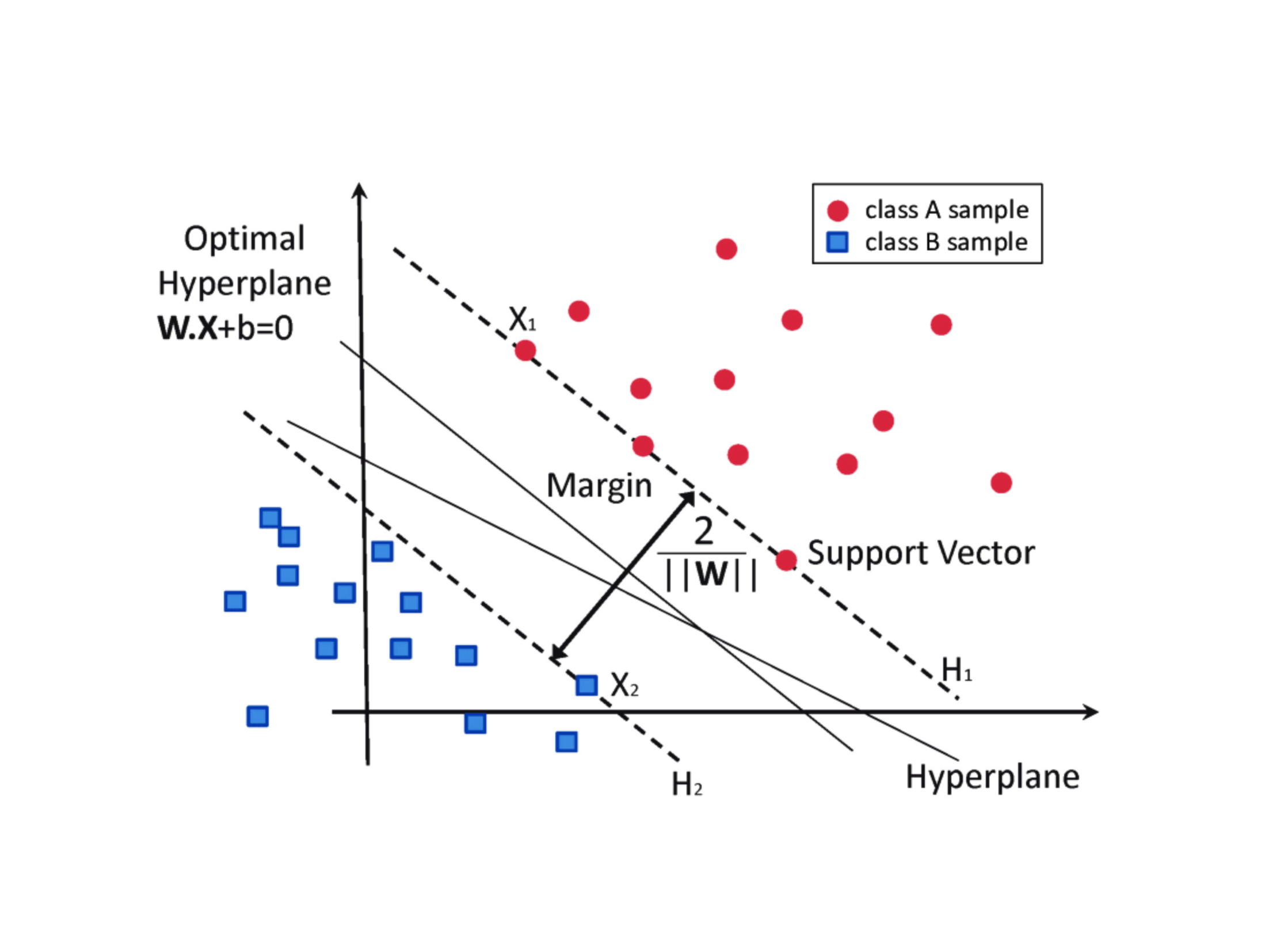
感知机只有输出层神经元进行激活函数处理, 即只拥有一层功能神经元 (functional neuron), 其学习能力非常有限, 事实上, 若两类模式是线性可分的, 即存在一个线性超平面能够将它们分开, 如下图所示, 则感知机的学习过程一定会收敛 (converge) 而求得适当的权向量 $w$; 否则感知机学习过程将会发生振荡, $w$ 难以稳定下来, 不能求得合适解.
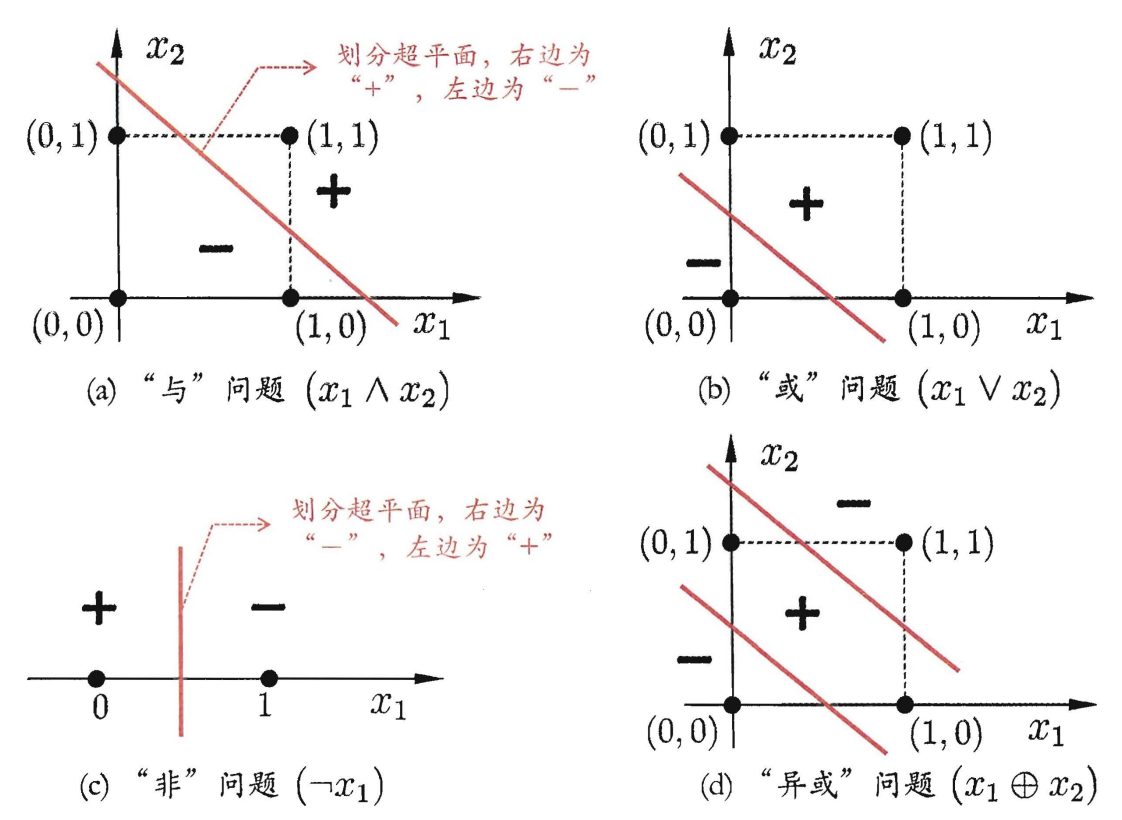
3. Multi-Layer Feedforward Nerual Networks
要解决非线性可分问题, 需考虑使用多层功能神经元. 例如下图这个简单的两层感知机就能解决异或问题.
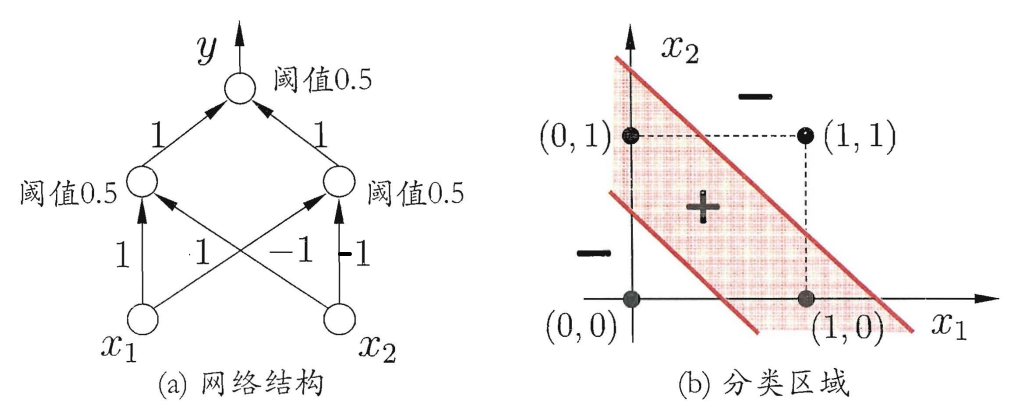
计算过程如下:
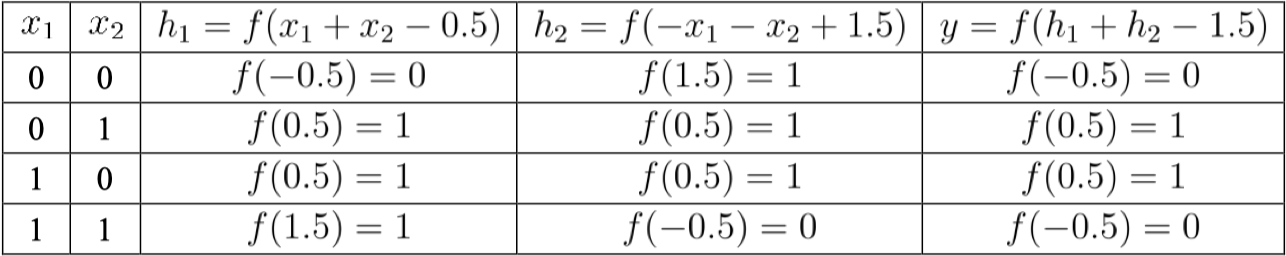
更一般的, 常见的神经网络是如下图所示的层级结构, 每层神经元与下一层神经元全互连, 神经元之间不存在同层连接, 也不存在跨层连接. 这样的神经网络结构通常称为多层前馈神经网络 (multi-layer feedforward neural networks). 神经网络的学习过程, 就根据训练数据来调整神经元之间的连接权 (connection weight) 以及每个功能神经元的阈值; 换言之, 神经网络学到的东西, 蕴含在连接权和阈值中.

4. Error Backpropogation
多层神经网络的学习能力要比单层感知机强很多, 但是要训练多层神经网络, 单层感知机的学习规则就显得不够用了, 因此我们在这里将会介绍误差逆传播 (Error BackPropagation) 算法. 下面我们来以一个单隐层神经网络为例来推导一下 BP 算法.
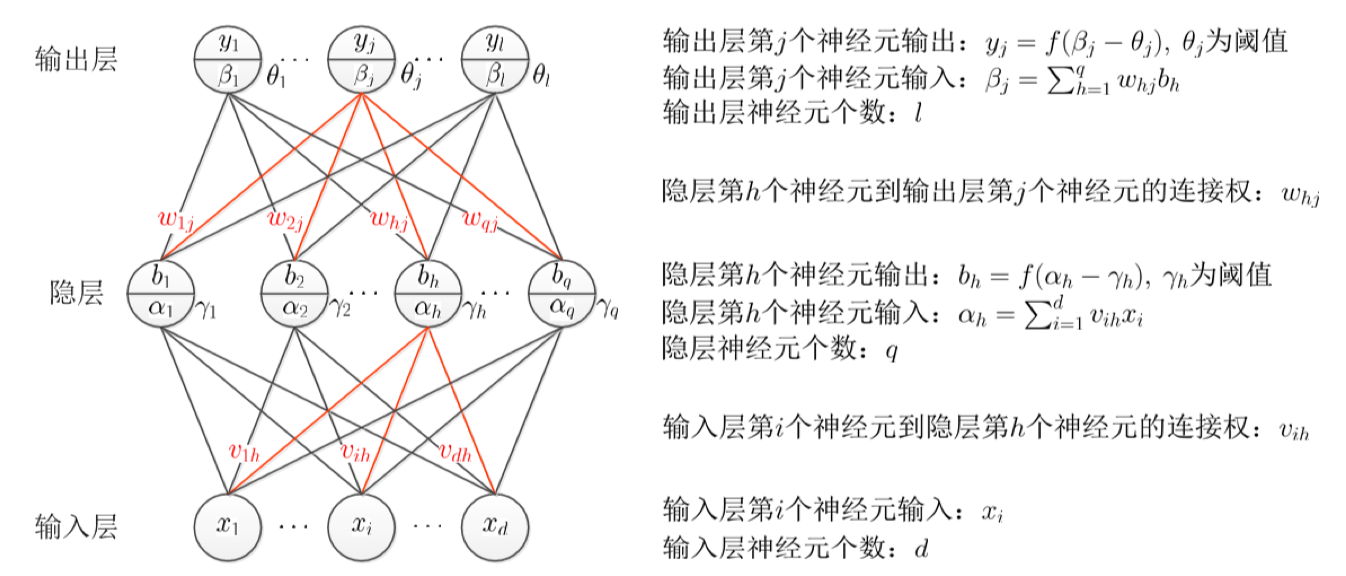
训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_m,y_m)\}$, 其中第 $k$ 个样本 $(\mathbf{x}_k,\mathbf{y}_k)$
假设隐层和输出层神经元都使用 Sigmoid 函数
待确定参数:
- 输入层到隐层的 $d\times q$ 个权值 $v_{ih}\ (1\leq i\leq d,\ 1\leq h\leq q)$
- 隐层到输出层的 $q\times l$ 个权值 $w_{hj}\ (1\leq h\leq q,\ 1\leq j\leq l)$
- 隐层的 $q$ 个神经元的阈值 $\gamma_h\ (1\leq h \leq q)$
- 输出层的 $l$ 个神经元的阈值 $\theta_j \ (1\leq j \leq l)$
另外, 隐层的神经元个数 $q$ 以及训练轮数 epoch 也都是需要确定的超参数.
BP 算法首先在 $(0,1)$ 范围内随机初始化网络中所有连接权和阈值, 在每一轮迭代中采用梯度下降策略逐步对权重进行更新, 而标准 BP 算法在每一轮迭代中是依次仅针对一个训练样例更新连接权和阈值.
现在我们来开始推导 BP 算法. 首先, 神经网络在一个训练样例 $(\mathbf{x}_k,\mathbf{y}_k)$ 上的均方误差为:
任意参数的更新估计式为:
BP 算法基于梯度下降策略, 以目标的负梯度方向对参数进行调整. 对式 (5.4) 的误差 $E_k$, 给定学习率 $\eta$, 有:
根据导数运算的规律, 我们能够得到:
其中:
同理, 我们能够得到:
其中:
按照这种思路继续往前推, 我们能得到 $\frac{\partial E_k}{\partial v_{ih}}$ 的计算公式:
其中:
$\frac{\partial E_k}{\partial \gamma_h}$ 的推导也同上, 在这里我就不赘述了. 到此, 我们的 BP 算法的推导就完成了! 但是你有没有觉得这种单个参数的计算太麻烦了!!! 我们不妨借用矩阵来使我们的运算更方便!
4.1 Matrix Solution
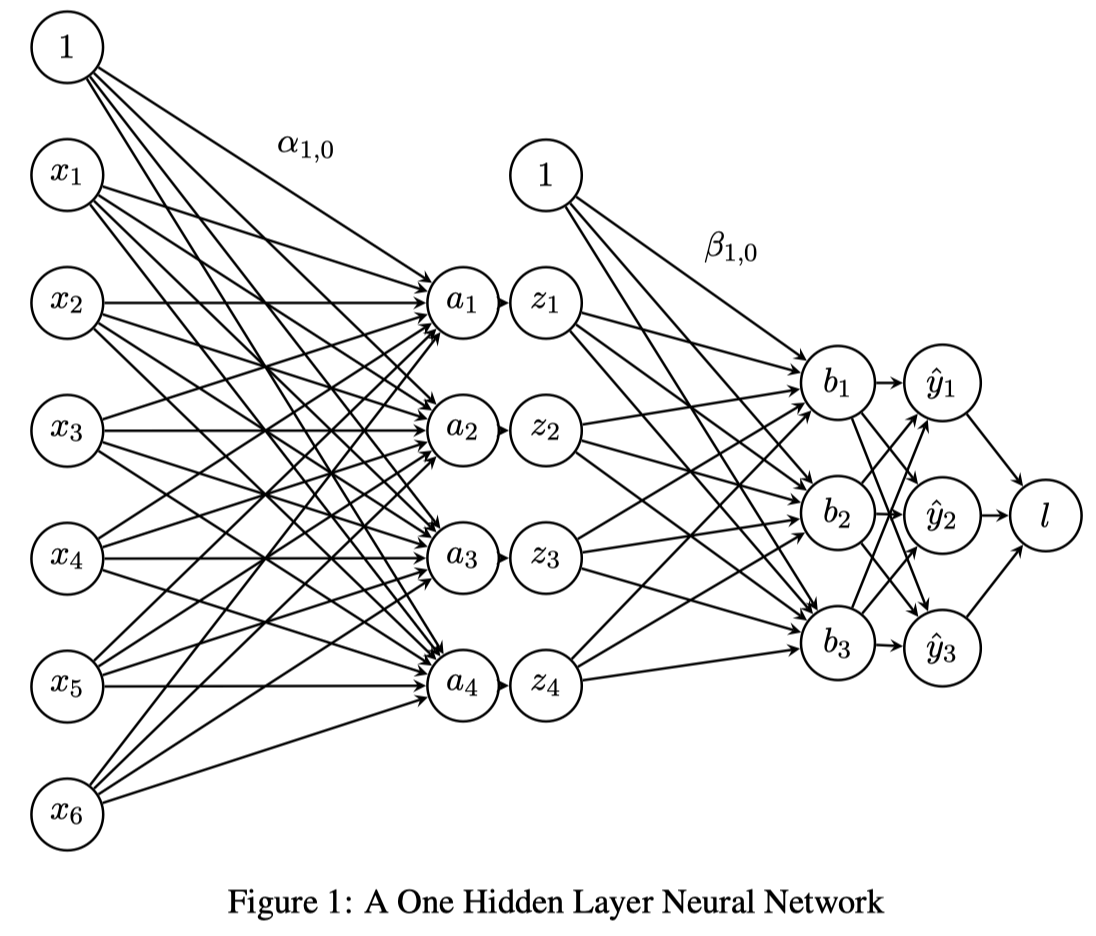
Network Overview
输入层有 6 个特征: $\mathbf{x}=[x_1,…,x_6]^T$
隐层有 4 个神经元: $\mathbf{z}=[z_1,…,z_4]^T$
输出层是一个概率分布: $\mathbf{y}=[y_1,y_2,y_3]^T$
We also allow for a bias term by adding a constant one to the input, $x_0=1$ and a constant one to the hidden layer $z_0=1$.
$\alpha$ 是从输入层到隐层的权重矩阵. $\beta$ 是隐层到输出层的参数矩阵.
$\alpha_{j,i}$ represents the weight going to the node $z_j$ in the hidden layer from the node $x_i$ in the input layer (e.g. $\alpha_{1,2}$ is the weight from $x_2$ to $z_1$ ), and $\beta$ is defined similarly. We will use a sigmoid activation function for the hidden layer and a softmax for the output layer.
Network Details Equivalently, we define each of the following.
The input:

Linear combination at the first (hidden) layer:
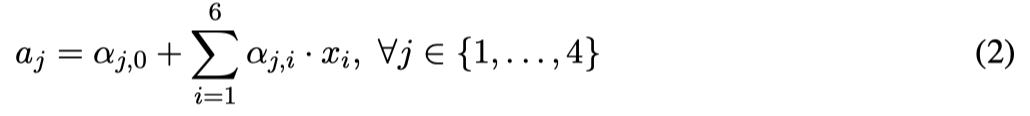
Activation at the first (hidden) layer:
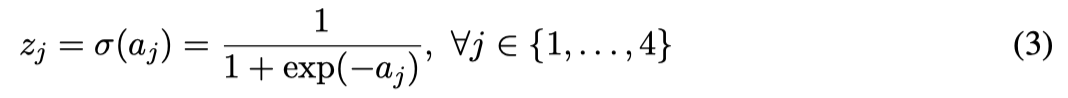
Linear combination at the second (output) layer:
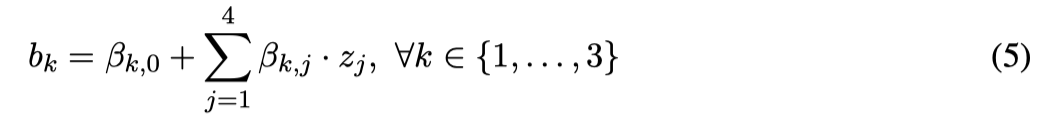
Activation at the second (output) layer:
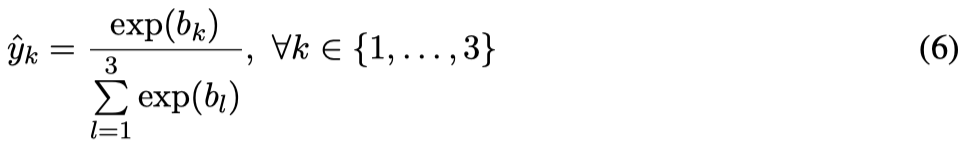
不含 bias 参数的 $\alpha$:

不含 bias 参数的 $\beta$:
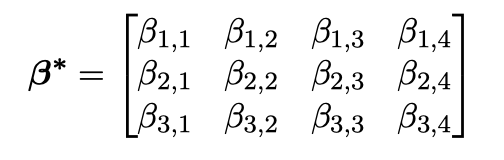
含 bias 参数的 $\alpha$:

含 bias 参数的 $\beta$:
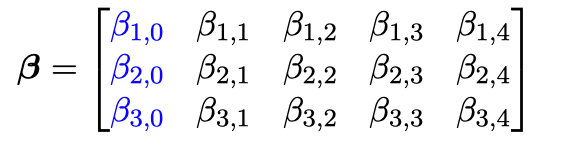
And we set our first value of our input vectors to always be 1 ($x_0=1$), so our input becomes:
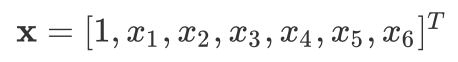
Loss
We will use cross entropy loss, $\ell(\hat{y},y)$. If $\mathbf{y}$ represents our target output, which will be a one-hot vector representing the correct class, and $\hat{\mathbf{y}}$ represents the output of the network, the loss is calculated by:
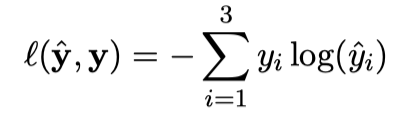
Feed Forward
$\mathbf{a}=\alpha\mathbf{x}$
$\mathbf{z}=sigmoid(\mathbf{a})$
$\mathbf{b}=\beta\mathbf{z}$
$\hat{\mathbf{y}}=softmax(\mathbf{b})$
Backpropagation
$\frac{\partial \ell}{\partial \mathbf{b}}=-\mathbf{y}+\hat{\mathbf{y}}$
$\frac{\partial \ell}{\partial \beta}=\frac{\partial \ell}{\partial \mathbf{b}}\mathbf{z}^T$
$\frac{\partial \ell}{\partial \mathbf{z}}=(\beta^{*})^T\frac{\partial \ell}{\partial \mathbf{b}}$
$\frac{\partial \ell}{\partial \mathbf{a}}=\frac{\partial \ell}{\partial \mathbf{z}}\odot\mathbf{z}\odot(1-\mathbf{z})$
$\frac{\partial \ell}{\partial \alpha}=\frac{\partial \ell}{\partial \mathbf{a}}\mathbf{x}^T$
符号 $\odot$ 表示矩阵哈达玛积, 即两个大小相同的矩阵对应位置元素相乘.