防止过拟合-正则化(Regularization)

1. Introduction

正则化 (Regularization) 是机器学习中一种比较常用的技术, 其主要的目的是控制模型的复杂度, 减小过拟合的可能性, 增加模型的泛化能力.

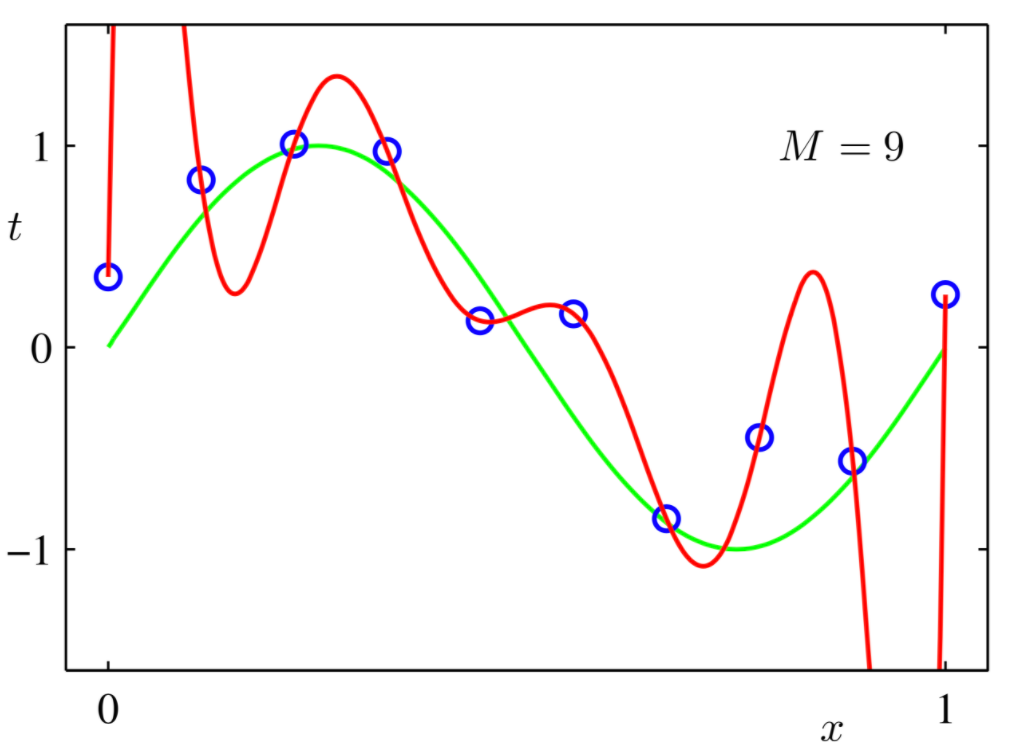
如上图, 红色这条“想象力”过于丰富上下横跳的曲线就是过拟合情形. 结合上图和正则化的英文 Regularizaiton-Regular-Regularize, 直译应该是: 规则化. 什么是规则? 你妈喊你6点前回家吃饭, 这就是规则, 一个限制. 同理, 在这里, 规则化就是说给需要训练的目标函数加上一些规则 (限制), 让他们不要自我膨胀. 正则化, 看起来, 挺不好理解的, 追其根源, 还是“正则”这两字在中文中实在没有一个直观的对应, 如果能翻译成规则化, 更好理解.

最基本的正则化方法是在原目标 (代价) 函数中添加惩罚项, 对复杂度高的模型进行“惩罚”. 其数学表达形式为:

$$\widetilde{J}(w;X,y)=J(w;X,y)+\alpha\Omega(w)$$

式中 $X,y$ 为训练样本和相应标签, $w$ 为权重系数向量; $J()$ 为目标函数, $\Omega()$ 即为惩罚项, 可以理解为模型”规模”的某种度量; 参数 $\alpha$ 控制正则化强弱. 不同的 $\Omega$ 函数对权重 $w$ 的最优解有不同的偏好, 因而会产生不同的正则化效果. 最常用的 $\Omega$ 函数有两种, 即 $l_1$ 范数和 $l_2$ 范数, 相应称之为 $l_1$ 正则化和 $l_2$ 正则化, 此时有:

$$\begin{aligned} &l_1:\Omega=||w||_1=\sum_i|w_i| \\ &l_2:\Omega=||w||_2^2=\sum_iw_i^2 \end{aligned}$$

2. Math Explanation

我们可以从带约束条件的优化求解和最大后验概率两种思路来推导 $l_1,l_2$ 正则化.

1. 正则化理解之基于约束条件的最优化

   对于模型权重系数 $w$ 求解是通过最小化目标函数实现的, 即求解:

   $$\min_wJ(w;X,y)$$

   我们知道, 模型的复杂度可以用 VC 维来衡量. 通常情况下, 模型 VC 维与参数 $w$ 的个数成线性关系: 即 $w$ 数量越多, VC 维越大, 模型越复杂. 因此, 为了限制模型的复杂度, 很自然的思路是减少系数 $w$ 的个数, 即让 $w$ 向量中一些元素为 0 或者说限制 $w$ 中的非零元素个数. 为此, 我们可以在原优化问题中加入一个约束条件:

   $$\min_wJ(w;X,y) \\ s.t.||w||_0\le C$$

   $||·||_0$ 范数表示向量中非零元素的个数. 但由于该问题是一个 NP 问题且非凸函数, 不易求解, 为此我们需要稍微放松一下约束条件. 为了达到近似效果, 我们不严格要求某些权重 $w$ 为 0, 而是要求权重 $w$ 应该接近于 0, 即尽量小. 从而可以用 $l_1,l_2$ 范数来近似 $l_0$ 范数, 即:

   $$\min_wJ(w;X,y)\quad s.t.||w||_1\le C\\ \min_wJ(w;X,y)\quad s.t.||w||_2\le C$$

   使用 $l_2$ 范数时, 为了方便后续处理, 我们可以对 $||w||_2$ 进行平方, 此时只需要调整 $C$ 的取值即可. 利用拉格朗日算子法, 我们可以将上述带约束条件的最优化问题转换为不带约束项的优化问题, 构造拉格朗日函数:

   $$L(w,\alpha)=J(w;X,y)+\alpha(||w||_1-C) \\ L(w,\alpha)=J(w;X,y)+\alpha(||w||_2^2-C)$$

   其中 $\alpha>0$, 我们假设 $\alpha$ 的最优解为 $\alpha^*$, 则对拉格朗日函数求最小化等价于:

   $$\min_wJ(w;X,y)+\alpha^*||w||_1 \\ \min_wJ(w;X,y)+\alpha^*||w||_2^2 \\$$

   故此, 我们得到对 $l_1,l_2$ 正则化的第一种理解:

   • $l_1$ 正则化等价于在原优化目标函数中增加约束条件 $||w||_1\leq C$;
   • $l_2$ 正则化等价于在原优化目标函数中增加约束条件 $||w||_2^2\leq C$;

2. 正则化理解之最大后验概率估计

   在最大似然估计中, 是假设权重 $w$ 是未知的参数, 从而求得对数似然函数:

   $$l(w)=\log[P(y|X;w)]=\log[\prod_iP(y_i|x_i;w)]$$

   通过假设 $y^i$ 的不同概率分布, 即可得到不同的模型. 例如若假设 $y_i\thicksim N(w^Tx_i,\sigma^2)$ 的高斯分布, 则有:

   $$l(w)=\log[\prod_i\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y_i-w^Tx_i)^2}{2\sigma^2})]=-\frac{1}{2\sigma^2}\sum_i(y_i-w^Tx_i)^2+C$$

   式中 $C$ 为常数项, 由于常数项和系数项不影响 $\max l(w)$ 的解, 因而可令 $J(w;X,y)=-l(w)$ 即可得到线性回归的代价函数.

   在最大后验概率估计中, 是将权重 $w$ 看作随机变量, 也具有某种分布, 从而有:

   $$P(w|X,y)=\frac{P(w,X,y)}{P(X,y)}=\frac{P(X,y|w)P(w)}{P(X,y)}\propto P(y|X,w)P(w)$$

   同时取对数有:

   $$\mathbf{MAP}=\log P(y|X,w)P(w)=\log P(y|X,w)+\log P(w)$$

   可以看出, 后验概率函数在似然函数的基础之上增加了一项 $\log P(w)$. $P(w)$ 的意义是对权重系数 $w$ 的概率分布的先验假设, 在收集到训练样本 $\{X,y\}$ 后, 则可根据 $w$ 在 $\{X,y\}$ 下的后验概率对 $w$ 进行修正, 从而做出对 $w$ 更好的估计.

   • 若假设 $w_j$ 的先验分布为均值是 0 的高斯分布, 即 $w_j\thicksim N(0,\sigma^2)$, 则有:

     $$\log P(w)=\log\prod_jP(w_j)=\log\prod_j\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{w_j^2}{2\sigma^2})=-\frac{1}{2\sigma^2}\sum_jw_j^2+C'$$

     可以看到, 在高斯分布下 $\log P(w)$ 的效果等价于在代价函数中增加 $l_2$ 正则项.

   • 若假设 $w_j$ 的先验分布是均值为 0, 参数为 $a$ 的拉普拉斯分布, 即:

     $$P(w_j)=\frac{1}{\sqrt{2a}}\exp(-\frac{|w_j|}{a})$$

     则有:

     $$\log P(w)=\log\prod_j\frac{1}{\sqrt{2a}}\exp(-\frac{|w_j|}{a})=-\frac{1}{a}\sum_j|w_j|+C'$$

     可以看到, 在拉普拉斯分布下 $\log P(w)$ 的效果等价于在代价函数中增加 $l_1$ 正则项.

   故此, 我们得到对于 $l_1,l_2$ 正则化的第二种理解:

   • $l_1$ 正则化可以通过假设权重 $w$ 的先验分布为拉普拉斯分布, 由最大后验概率估计导出;

• $l_2$ 正则化可以通过假设权重 $w$ 的先验分布为高斯分布, 由最大后验概率估计导出;

3. Effect Analysis

我们从直观分析和理论推导两个角度来说明 $l_1,l_2$ 正则化的效果.

1. 直观理解

   考虑带约束条件的优化解释, $l_2$ 正则化为:

   $$\min_wJ(w;X,y)\quad s.t.||w||_2^2\le C$$

   该问题的求解示意图如下:

   

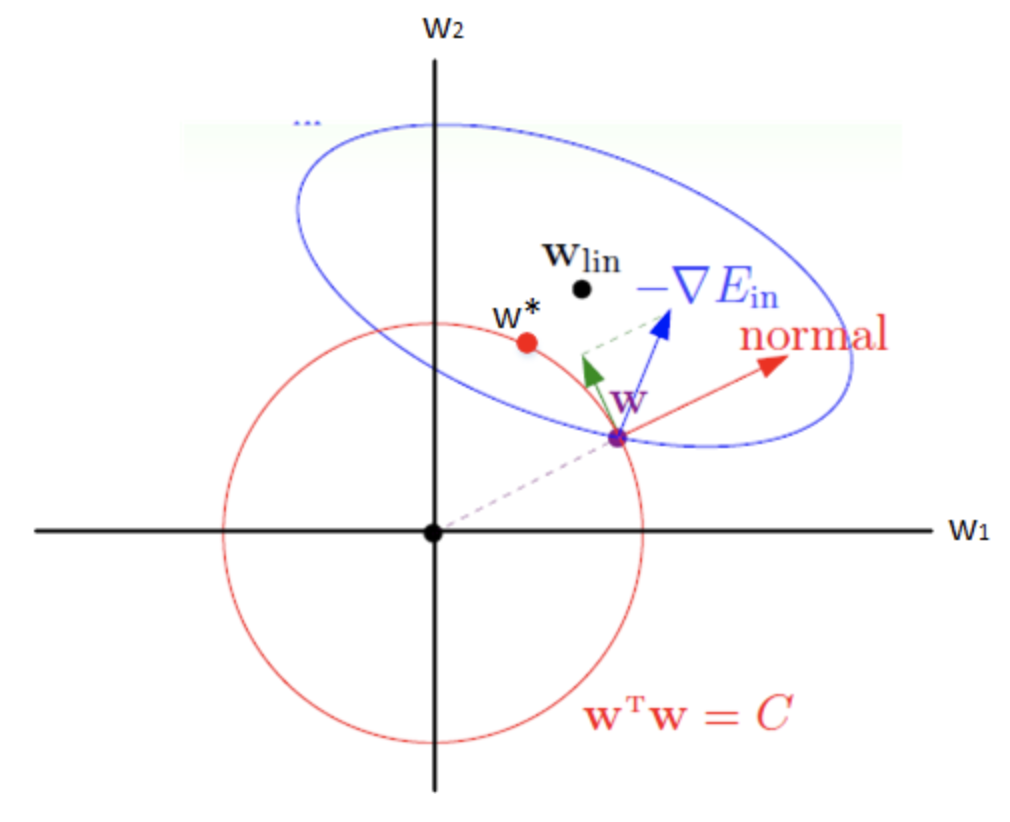
   图中椭圆为原目标函数 $J(w)$ 的一条等高线, 圆为半径 $\sqrt{C}$ 的范数球. 由于约束条件的限制, $w$ 必须位于 $l_2$ 范数球内. 考虑边界上的一点 $w$, 图中蓝色箭头为 $J(w)$ 在该处的梯度方向 $\nabla J(w)$, 红色箭头为 $l_2$ 范数球在该处的法线方向. 由于 $w$ 不能离开边界 (否则违反约束条件), 因而在使用梯度下降更新 $w$ 时, 只能朝着 $\nabla J(w)$ 在范数球上 $w$ 处的切线方向更新, 即图中的绿色箭头方向. 如此 $w$ 将沿着边界移动, 当 $\nabla J(w)$ 与范数球上 $w$ 处的法线平行时, 此时 $\nabla J(w)$ 在切线方向的分量为 0, $w$ 将无法继续移动, 从而达到最优解 $w^*$ (图中红点所示).

   为什么 $l_2$ 正则化对应的是一个圆?

   考虑 $z=w_1^2+w_2^2$ 就是抛物面, 俯视图是一个圆.

   考虑带约束条件的优化解释, $l_1$ 正则化为:

   $$\min_wJ(w;X,y)\quad s.t.||w||_1\le C\\$$

   该问题的求解示意图如下:

   

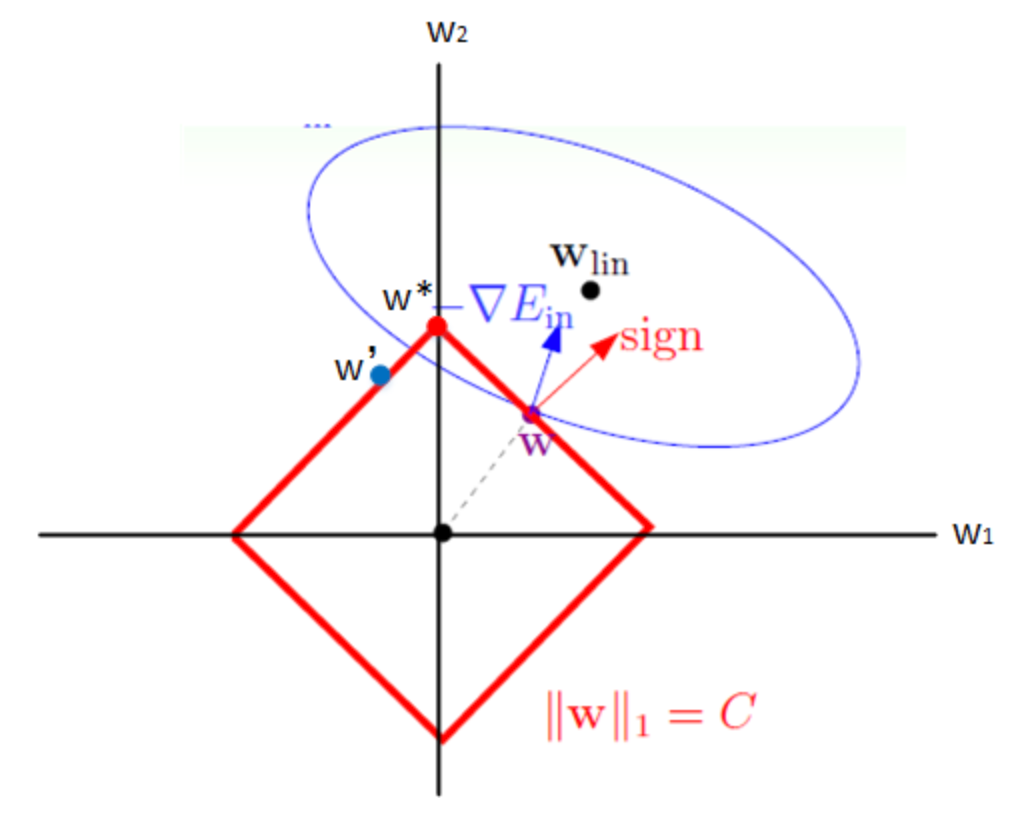
   其主要差别在于 $l_1,l_2$ 范数球的形状差异. 由于此时每条边界上 $w$ 的切线方向和法线方向保持不变, 在图中 $w$ 将一直朝着 $\nabla J(w)$ 在切线上的分量沿着边界向左上移动. 当 $w$ 跨过顶点到达 $w’$ 时, $\nabla J(w)$ 在切线方向的分量变为右上方, 因而 $w$ 将朝着右上方移到. 最终, $w$ 将稳定在顶点处, 达到最优解 $w^*$. 此时, 可以看到 $w_1=0$, 这也就是采用 $l_1$ 范数会使 $w$ 产生稀疏性的原因.

   以上分析虽是基于二维的情况, 但不难将其推广到多维情况, 其主要目的是为了直观说明 $l_1$ 和 $l_2$ 正则化最优解的差异, 以及 $l_1$ 范数为什么产生稀疏性.

   Question: 为什么 $l_1$ 正则会到达w’呢? 感觉如图的形式, 可能在到达上面的顶点前就能有一个最优解, 就是梯度下降方向与法向量平行?

   Answer: 这种情况是可能会出现的, 但可能性比较小, 而且实际数据维度比较大, 不太容易出现.

2. 理论推导

   数学功力不够暂时搞不懂, 之后补上…