隐马尔可夫模型(HMM)

HMM 是可以用于标注问题的统计数学模型, 描述由隐藏的马尔科夫链随机生成观测序列的过程, 属于生成模型. HMM模型在语音识别、自然语言处理、生物信息、模式识别等领域有广泛的应用.

使用HMM模型来解决的问题一般有两个特征:

1. 问题是基于序列的, 比如时间序列、状态序列.
2. 问题中有两类数据, 一类序列数据是可以观测到的, 即观测序列; 而另一类数据是不能观察到的, 即隐藏状态序列, 简称状态序列.

如果问题有了这两个特征, 那么这个问题一般可以使用HMM模型尝试解决, 这样的问题在生活中是很多的. 例如, 说一句话, 发出的声音是观测序列, 想表达的意思是隐藏状态序列.

1. Introduction

隐马尔科夫模型是关于时序的概率模型, 描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列, 再由各个状态生成一个观测而产生观测随机序列的过程. 隐藏的马尔科夫链随机生成的状态的序列, 称为状态序列 (state sequence); 每个状态生成一个观测, 而由此产生的观测的随机序列, 称为观测序列 (observation sequence).

隐马尔可夫模型由初始概率分布 ($\pi$), 状态转移概率分布 (A) 以及观测概率分布 (B) 确定. 隐马尔可夫模型的形式定义如下:

数学表达	解释
$Q=\{q_1,q_2,…,q_N\}$	所有可能的状态集合, 状态总数为 $N$
$V=\{v_1,v_2,…,v_M\}$	所有可能的观测集合, 观测总数为 $M$
$I=(i_1,i_2,…,i_T)$	长度为 $T$ 的状态序列
$O=(o_1,o_2,…,o_T)$	长度为 $T$ 的观测序列
$A=[a_{ij}]_{N\times N}$	状态转移概率矩阵 (Transition Probability Matrix)
$B=[b_j(k)]_{N\times M}$	发射概率矩阵 (Emission Probability Matrix)
$\pi=(\pi_i)$	初始状态概率向量

隐马尔可夫模型由 $\pi,A,B$ 共同决定. 其中 $\pi,A$ 决定状态序列, $B$ 决定观测序列. 因此马尔可夫模型 $\lambda$ 可以用三元符号表示, 即

$$\lambda=(\pi,A,B)$$

HMM 模型有两个假设:

• 齐次马尔科夫假设

  将马尔科夫假设作用于状态序列, 假设当前状态 $i_t$ 仅仅依赖于前一个状态 $i_{t-1}$, 连续多个状态构成隐马尔科夫链, 数学表达式为:

  $$P(i_t|i_{t-1},o_{t-1},i_{t-2},o_{t-2},i_{t-3},...,i_2,o_2,i_1,o_1)=P(i_t|i_{t-1})$$

• 输出独立性假设

  任意时刻的观测 $o_t$ 只依赖于该时刻的状态 $i_t$, 与其他时刻的状态或观测独立无关, 数学表达式为:

  $$P(o_t|o_1,...,o_t,...,o_T,i_1,...,i_t,...,i_T)=P(o_t|i_t)$$

再看一个 HMM 的例子:

假定你是一个在2799年研究地球暖化历史的气象学家, 你找不到在 2007 年夏天任何关于巴尔的摩, 马里兰州的天气的记录资料, 但是你发现了 Jason Eisner 的日记, 其中列出了在这个夏天的每一天他吃冰淇淋的数量. 我们的目的是利用这些关于冰淇淋的数量来估计每一天的气温. 为了简单起见, 我们假定每一天的天气只有两种状态: 冷或热 (C or H). 这样一来, Eisner 的问题可以描述如下:

给定一个观察序列 O, 每一个观察是一个整数, 它对应于在某一给定的日子所吃冰淇淋的数量, 引起 Jason Eisner 吃冰淇淋的天气的状态序列是隐藏的, 这个隐藏的状态序列用 Q 表示, 它的值为 H 或 C.

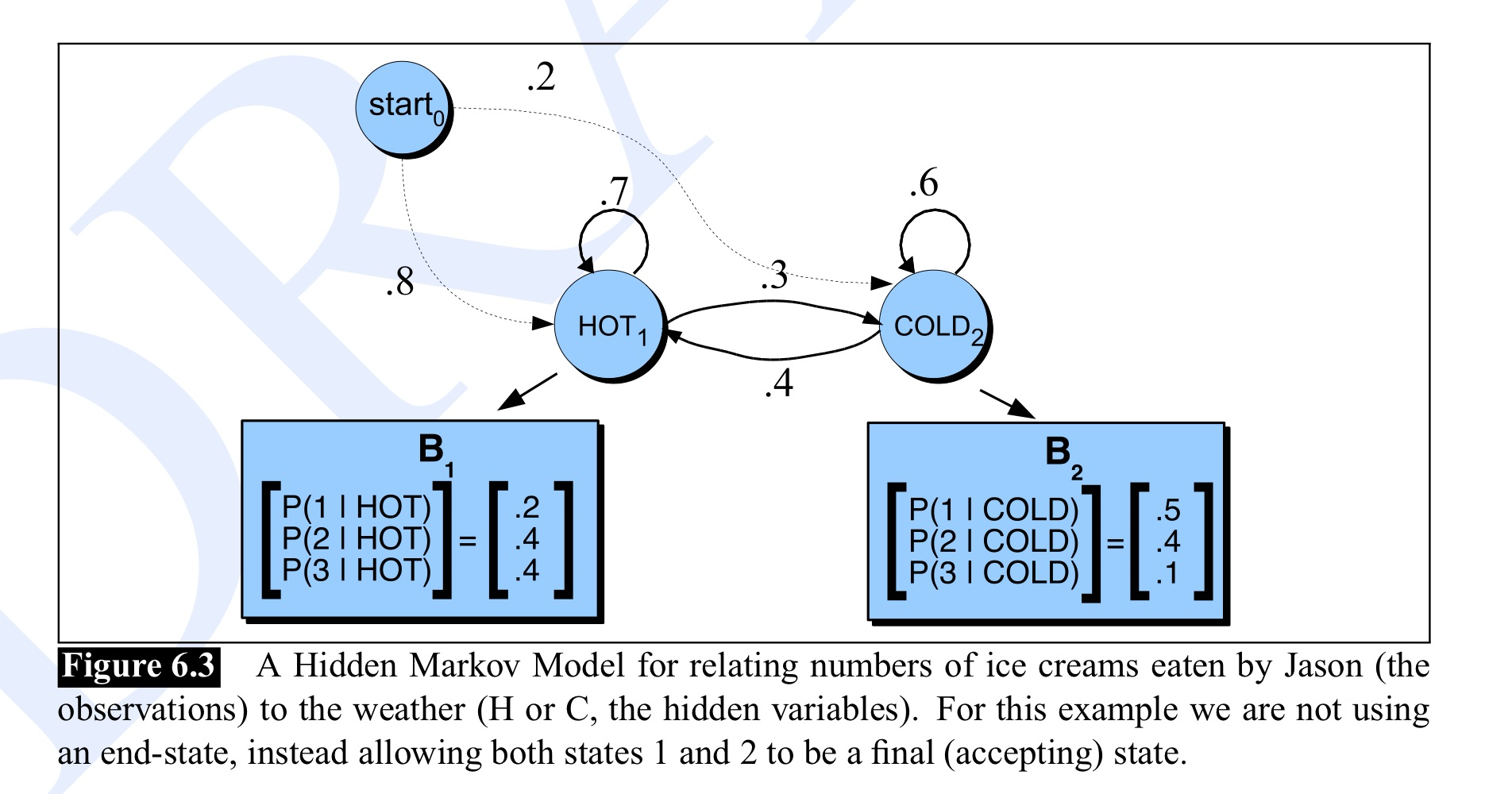
天气对应状态, 状态的集合是:

$$Q=\{HOT,COLD\},N=2$$

所吃冰淇淋的数量对应观测, 观测的集合是:

$$V=\{1,2,3\},M=2$$

初始概率分布为:

$$\pi=(0.8,0.2)^T$$

状态转移概率分布为:

$$A=\left[\begin{matrix}0.7,0.3\\0.4,0.6\end{matrix}\right]$$

发射概率分布为:

$$B=\left[\begin{matrix}0.2,0.4,0.4\\0.5,0.4,0.1\end{matrix}\right]$$

2. Inference Problems

HMM 主要被用于解决以下几个问题:

1. Filtering Problem - Infering the present

   已知模型参数和一个观测序列 $O$, 求最后时刻各个隐含状态的概率分布, 即 $P(i_t|o_{1:t})$.

   代表模型: Kalman Filter (卡尔曼滤波器)

2. Smoothing Problem - Infering the past

   已知模型参数和一个观测序列 $O$, 求中间某时刻各个隐含状态的概率分布, 即 $P(i_t|o_{1:T}),t<T$.

3. Prediction Problem - Infering the future

   已知模型参数和一个观测序列 $O$, 求未来某时刻各个隐含状态的概率分布, 即 $P(i_t|o_{1:T}),t>T$.

4. Learning Problem

   已知观测序列 $O=(o_1,o_2,…,o_T)$, 估计模型 $\lambda=(A,B,\pi)$ 参数, 使得在该模型下观测序列概率 $P(O|\lambda)$ 最大, 即用极大似然估计的方法估计参数.

5. Likelihood Problem

   给定模型参数和一个观测序列 $O$, 求观测序列出现的概率, 即 $P(o_{1:T})$.

6. Decoding Problem

   已知模型参数和一个观测序列 $O$, 求对给定观测序列条件概率 $P(I|O)$ 最大的状态序列 $I$.

2.1 Filtering Problem

我们的目的是求 $P(i_t|o_{1:t})$, 很明显有:

$$P(i_t|o_{1:t})=\frac{P(i_t,o_{1:t})}{P(o_{1:t})}$$

且有:

$$\begin{equation}\begin{aligned}P(i_t|o_{1:t})=&P(i_t|o_t,o_{1:t-1})\\=&\alpha P(i_t,o_t|o_{1:t-1})\\=&\alpha\sum_{i_{t-1}}P(i_{t-1},i_t,o_t|o_{1:t-1})\\=&\alpha\sum_{i_{t-1}}P(i_{t-1}|o_{1:t-1})P(i_t|i_{t-1})P(o_t|i_t)\\=&\alpha P(o_t|i_t)\sum_{i_{t-1}}P(i_t|i_{t-1})P(i_{t-1}|o_{1:t-1})\end{aligned}\end{equation}$$

因此我们可以得到:

$$P(i_t,o_{1:t})=P(o_t|i_t)\sum_{i_{t-1}}P(i_t|i_{t-1})P(i_{t-1},o_{1:t-1})$$

因此我们可以先想办法求得, $P(i_t,o_{1:t})$, 也就是 un-nomarlized filtered posterior distribution. 我们可以利用 Forward Algorithm 来求解该项.

我们记, $\alpha_t(i)=P(o_1,…,o_t,i_t=q_i|\lambda)$, 这个公式表示的是在之前所有的观测变量的前提下求出当前时刻的隐含状态的概率, 图示如下:

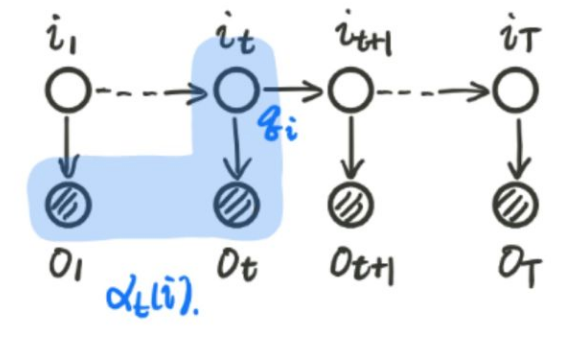
因此我们的思路就是递推求得前向概率 $\alpha_t(i)$, 最后求得 $P(O|\lambda)$.

其中, 不难得到:

$$\begin{equation}\begin{aligned}P(O|\lambda)=&P(o_{1:T})\\=&\sum_{i=1}^N\frac{P(i_T=q_i,o_{1:T})}{P(i_T=q_i|o_{1:T})}\\=&\sum_{i=1}^NP(i_T=q_i,o_{1:T})\\=&\sum_{i=1}^N\alpha_T(i)&\end{aligned}\end{equation}$$

Forward Algorithm

输入: $\lambda=(\pi,A,B)$, 观测序列 $O$

输出: 观测序列概率 $P(O|\lambda)$

(1) 初值

$$\alpha_1(i)=\pi_ib_i(o_1),\quad i=1,2,...,N$$

(2) 递推 对 $t=1,2,…,T-1$

$$\alpha_{t+1}(i)=[\sum_{j=1}^N\alpha_t(j)a_{ji}]b_i(o_{t+1}),\quad i=1,2,...,N$$

(3) 终止

$$P(O|\lambda)=\sum_{i=1}^N\alpha_T(i)$$

我们可以用一个图来进行表示:

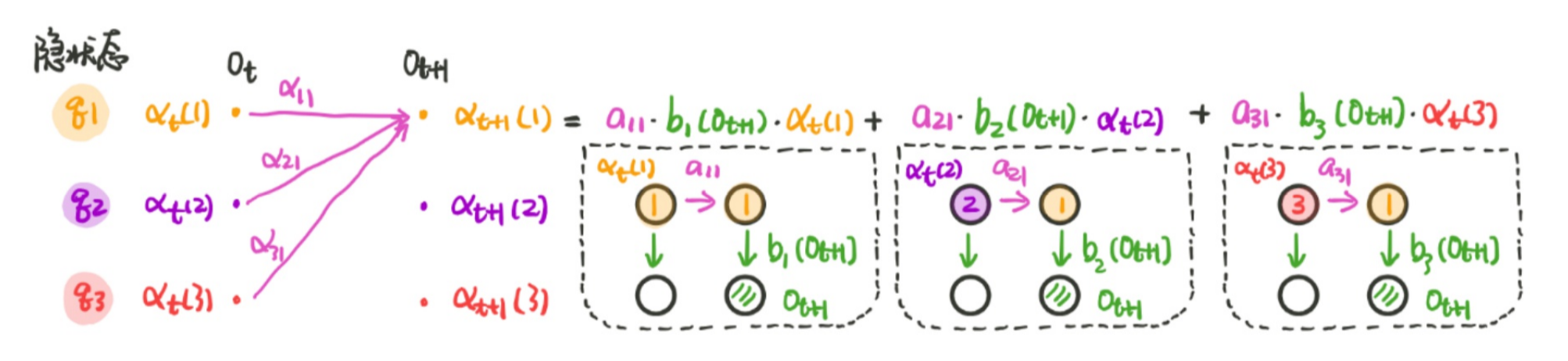
2.2 Smoothing Problem

为了解决 Smoothing Problem, 我们要引入另外一种算法: Backward Algorithm.

我们首先定义一个后向概率:

$$\beta_t(i)=P(o_{t+1},o_{t+2},...,o_T|i_t=q_i,\lambda)$$

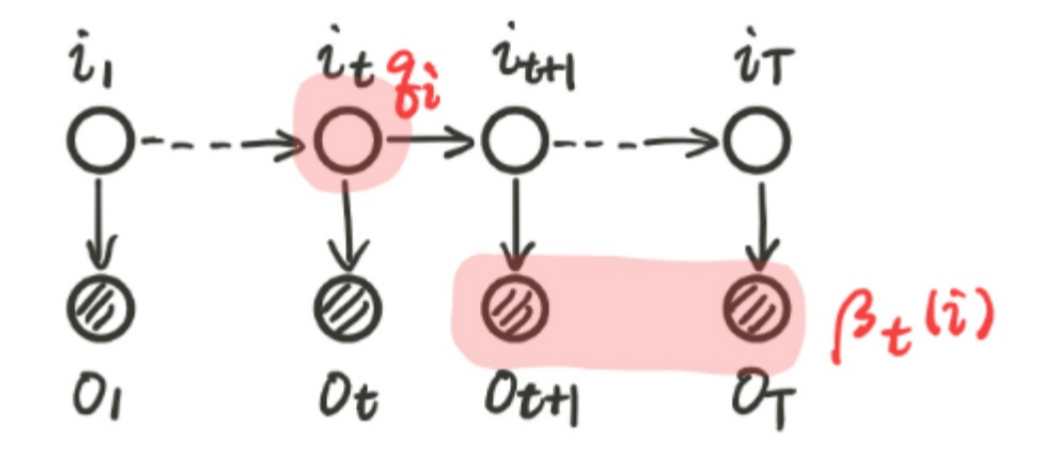
因此, 我们有 $\beta_1(i)=P(o_{2:T}|i_1=q_i,\lambda)$. 那么我们可以推导:

$$\begin{equation}\begin{aligned}P(O|\lambda)=&P(o_{1:T}|\lambda)\\=&\sum_{i=1}^NP(o_{1:T},i_1=q_i|\lambda)\\=&\sum_{i=1}^NP(o_{1:T}|i_1=q_i,\lambda)P(i_1=q_i|\lambda)\\=&\sum_{i=1}^NP(o_1|o_{2:T},i_1=q_i,\lambda)P(o_{2:T},i_1=q_i|\lambda)\pi_i\\=&\sum_{i=1}^NP(o_1|i_1=q_i,\lambda)\beta_1(i)\pi_i\\=&\sum_{i=1}^Nb_i(o_1)\pi_i\beta_1(i)\end{aligned}\end{equation}$$

因此, 我们有算法

Backward Algorithm

输入: $\lambda=(\pi,A,B)$, 观测序列 $O$

输出: 观测序列概率 $P(O|\lambda)$

(1) 初值

$$\beta_T(i)=1,\quad i=1,2,...,N$$

(2) 递推

对 $t=T-1,T-2,…,1$

$$\beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),\quad i=1,2,...,N$$

(3) 终止

$$P(O|\lambda)=\sum_{i=1}^Nb_i(o_1)\pi_i\beta_1(i)$$

因此, 针对 smoothing problem, 即 $P(i_t|o_{1:T}),t<T$, 我们可以推导:

$$\begin{equation}\begin{aligned}P(i_t,o_{1:T})=&P(i_t,o_{1:t})P(o_{t+1:T}|i_t,o_{1:t})\\=&P(i_t,o_{1:t})P(o_{t+1:T}|i_t)\\=&\alpha_t(i)\beta_t(i)\end{aligned}\end{equation}$$

进而

$$P(i_t|o_{1:T})=\frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^N\alpha_t(j)\beta_t(j)}$$

我们还可以进一步延展: 给定模型 $\lambda$ 和观测序列 $O$, 我们要求在时刻 $t$ 处于状态 $q_i$ 且在时刻 $t+1$ 处于状态 $q_j$ 的概率, 即 $P(i_t=q_i,i_{t+1}=q_j|o_{1:T})$, 我们可以推导得到:

$$\begin{equation} \begin{aligned} P(i_t=q_i,i_{t+1}=q_j|o_{1:T})=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{i=1}^N\sum_{j=1}^N\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)} \end{aligned} \end{equation}$$

2.3 Prediction Problem

我们这里只给出 one-step ahed predictive distribution:

$$\begin{equation} \begin{aligned} P(o_{t+1}|o_{1:t})=&\sum_{i_t,i_{t+1}}P(i_t,i_{t+1},o_{t+1}|o_{1:t}) \\ =&\sum_{i_t,i_{t+1}}P(o_{t+1}|i_{t},i_{t+1},o_{1:t})P(i_{t+1}|i_{t},o_{1:t})P(i_t|o_{1:t}) \\ =&\sum_{i_t,i_{t+1}}P(o_{t+1}|i_{t+1})P(i_{t+1}|i_t)P(i_t|o_{1:t}) \end{aligned} \end{equation}$$

2.4 Learning Problem

因为目前我还没有系统的学习过 EM 算法, 所以在这里先给出监督学习方法, 即用极大似然估计来估计隐马尔可夫的参数, 具体方法如下:

1. 初始状态概率 $\pi_i$

   $$\hat{\pi}_i=P(i_1=q_i)=\frac{N_{i_1=q_i}+1}{\sum_{j=1}^N(N_{i_1=q_j}+1)}$$

2. 转移状态概率分布 $a_{ij}$

   $$\hat{a}_{ij}=P(i_t=q_j|i_{t-1}=q_i)=\frac{N_{i_t=q_j,i_{t-1}=q_i}+1}{\sum_{p=1}^N(N_{i_t=q_p,i_{t-1}=q_i}+1)}$$

3. 发射概率分布 $b_j(k)$

   $$\hat{b}_j(k)=P(o_t=v_k|i_t=q_j)=\frac{N_{o_t=v_k,i_t=q_j}+1}{\sum_{p=1}^M(N_{o_t=v_p,i_t=q_j}+1)}$$

2.5 Likelihood Problem

我们在之前的推导中已经给出了公式:

$$P(O|\lambda)= \sum_{i=1}^N\alpha_T(i)\\ P(O|\lambda) = \sum_{i=1}^Nb_i(o_1)\pi_i\beta_1(i)\\ P(O|\lambda) = \sum_{i=1}^N\sum_{j=1}^N\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j), \quad t=1,2,...,T-1$$

2.6 Decoding Problem

HMM 的解码算法有两种: 近似算法 (Approximation Algorithm)和维特比算法 (Viterbi Algorithm).

2.6.1 Approximation Algorithm

近似算法其实是采取了我们在 Smoothing Problem 中所介绍的公式, 即 $P(i_t|o_{1:T}),t<T$.

其想法是: 在每个时刻 $t$ 选择在该时刻最有可能出现的状态 $i_t^{*}$, 从而得到一个状态序列 $I^=(i_1^{\},i_2^{*},…,i_T^{*})$, 并将其作为预测的结果.

给定隐马尔可夫模型 $\lambda$ 和观测序列 $O$, 在时刻 $t$ 处于状态 $q_i$ 的概率 $\gamma_t(i)$ 是:

$$\gamma_t(i)=P(i_t|o_{1:T})=\frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^N\alpha_t(j)\beta_t(j)}$$

根据最小化贝叶斯风险准则, 在每一时刻最可能的状态 $i_t^*$ 是:

$$i_t^*=\mathop{\arg\max}\limits_{1\le i\le N}[\gamma_t(i)],\quad t=1,2,...,T$$

备注: 这也是我在项目 https://github.com/alvisdeng/NLP-NER-Recognizer-with-HMMs 中使用的方法. 有很多math tricks 比如说在 log space 来进行计算, 具体可以参见 description.pdf 中的说明.

2.6.2 Viterbi Algorithm

[To be done]