鸡生蛋 or 蛋生鸡: EM 算法

1. Gaussian Single Model

我们先简单回顾一下经典的高斯模型. 一维高斯分布的概率密度函数如下:

$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$$

譬如将男生身高视为变量 $X$, 假设男生的身高服从高斯分布, 则 $X\sim N(\mu,\sigma^2)$, 女生亦如此. 只是男女生身高分布可能具有不同的均值和方差.

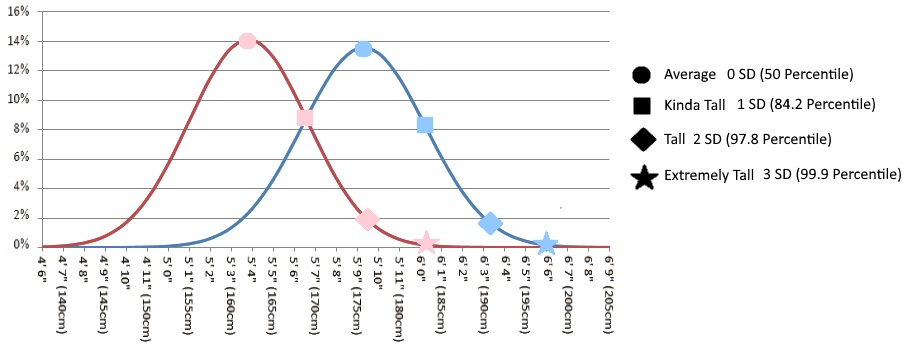
但有些时候数据并不是一维的而是多维的, 因此我们再来看一下多维高斯分布的概率密度函数. 多维变量 $X=(x_1,x_2,…,x_n)$ 的联合概率密度函数为:

$$f(X)=\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}}\exp[-\frac{1}{2}(X-\mu)^T\Sigma^{-1}(X-\mu)]$$

其中:

• d: 表示变量维度, 比如我们身高中的例子中 $d=1$.

• $\mu$: 表示各个变量的均值, $\mu=(\mu_1,\mu_2,…,\mu_n)$.

• $\Sigma$: 协方差矩阵, 描述各维变量之间的相关度. 对于二维高斯分布, 我们有

  $$\Sigma= \begin{equation} \left( \begin{array}{cc} \delta_{11} & \delta_{12}\\ \delta_{21} & \delta_{22} \end{array} \right) \end{equation}$$

我们看几个二维高斯分布的例子:

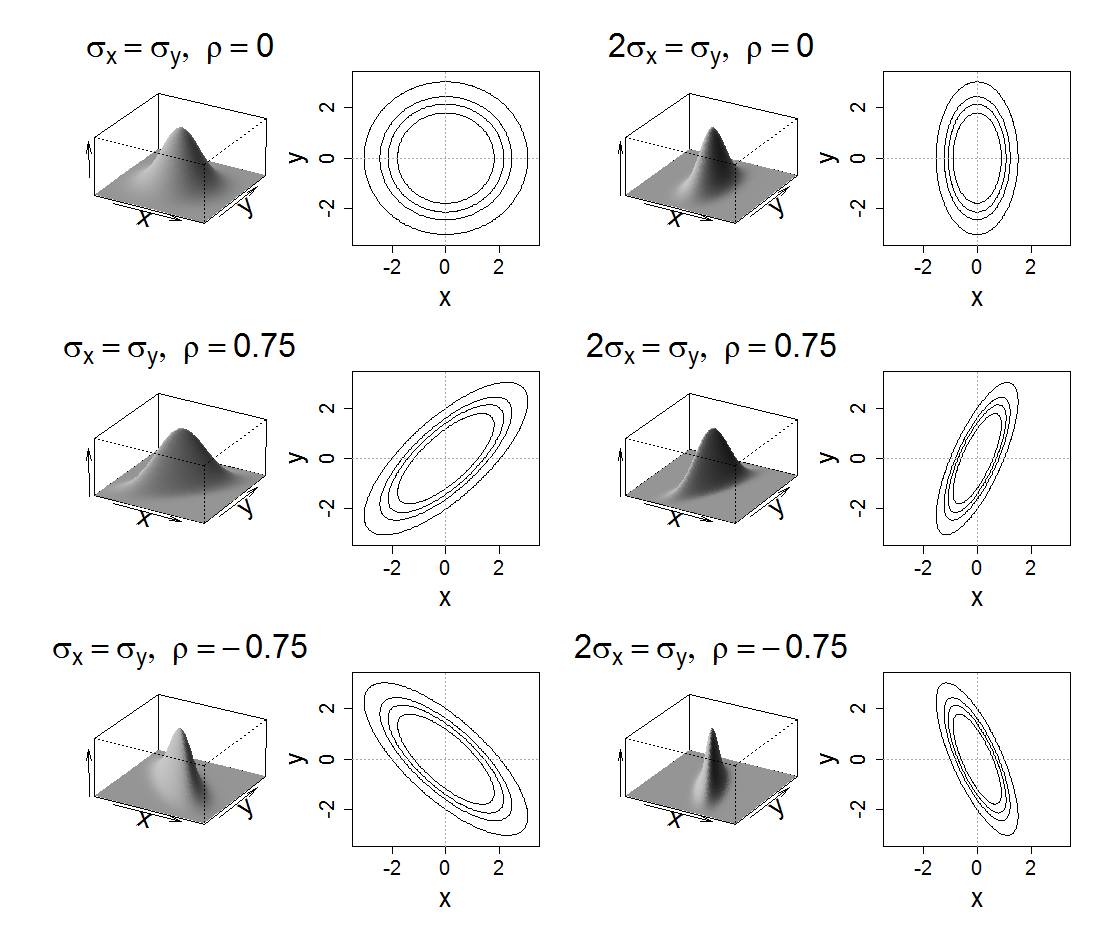
关于各个变量对于图像形状的影响我们则有以下总结:

1. 均值表征的是各维变量的中心, 其对二维高斯曲面的影响较好理解, 它使得整个二维高斯曲面在xoy平面上移动;
2. 协方差矩阵对角线上的两个元素, 即 $\delta_{11},\delta_{22}$ 是x维和y维变量的方差, 决定了整个高斯曲面在某一维度上的“跨度”, 方差越大, “跨度”越大;
3. 协方差矩阵斜对角线上的两个元素, 即 $\delta_{12}=\delta_{21}$ 是各维变量之间的相关性. 若其大于0, 则说明 $x$ 和 y 正相关, 小于0, 则负相关, 等于0, 则不相关. 绝对值大小则衡量了相关程度.

2. Gaussian Mixture Model

我们先来看一组数据, 数据的生成代码如下:

import numpy as np
import matplotlib.pyplot as plt

mean1 = [0,0]
cov1 = [[1,0],
        [0,3]]
data1 = np.random.multivariate_normal(mean1,cov1,200)

mean2 = [5,5]
cov2 = [[3,-0.5],
        [-0.5,1]]
data2 = np.random.multivariate_normal(mean2,cov2,200)


x1,y1 = data1.T
x2,y2 = data2.T

plt.figure(figsize=(12,10))
plt.scatter(x1,y1,marker="+",c='b',s=10)
plt.scatter(x2,y2,marker="*",c='r',s=10)
plt.axis()
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((-3,10))
plt.ylim((-5,8))
plt.xticks(np.arange(-3,11,1))
plt.yticks(np.arange(-5,9,1))
plt.show()

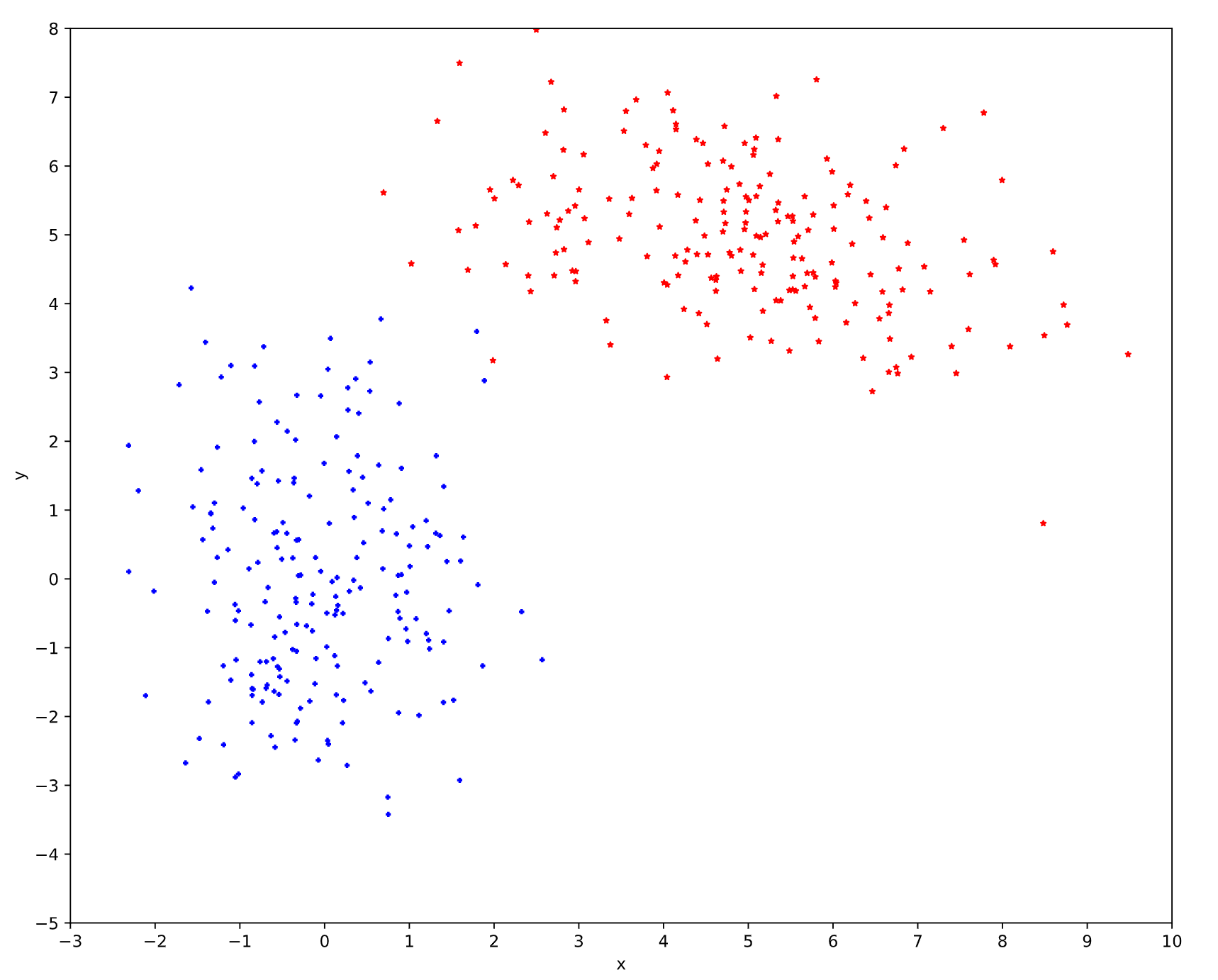
我们现在假设这个数据是由某个单独的高斯分布产生的, 我们利用 MLE 对这个高斯分布做参数估计, 得到一个最佳的高斯分布模型如下:

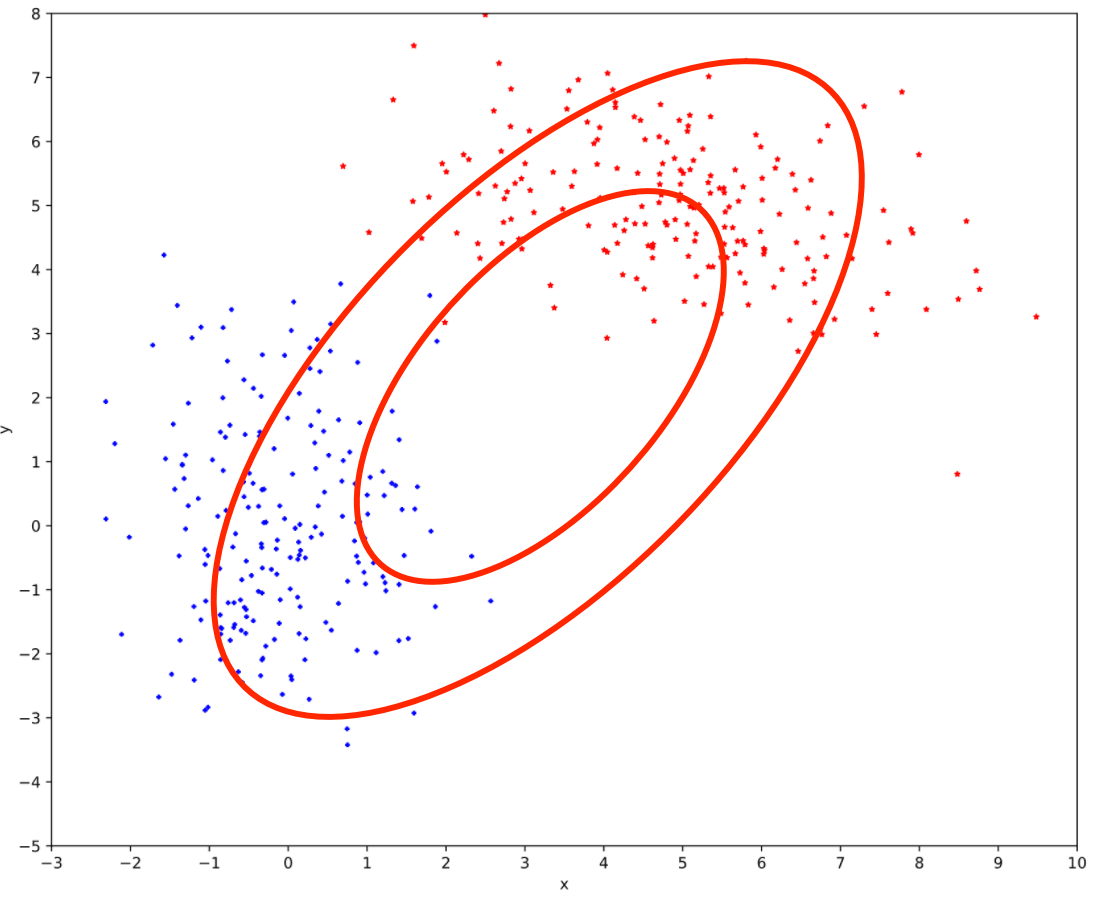
但这明显是存在问题的, 因为一般来讲越靠近椭圆的中心样本出现的概率越大, 这是由概率密度函数决定的, 但是这个高斯分布的椭圆中心的样本量却极少, 显然样本服从单高斯分布的假设并不合理, 单高斯模型无法产生这样的样本. 而根据我们产生数据的代码, 我们知道这是由两个不同的高斯分布模型所产生的数据.

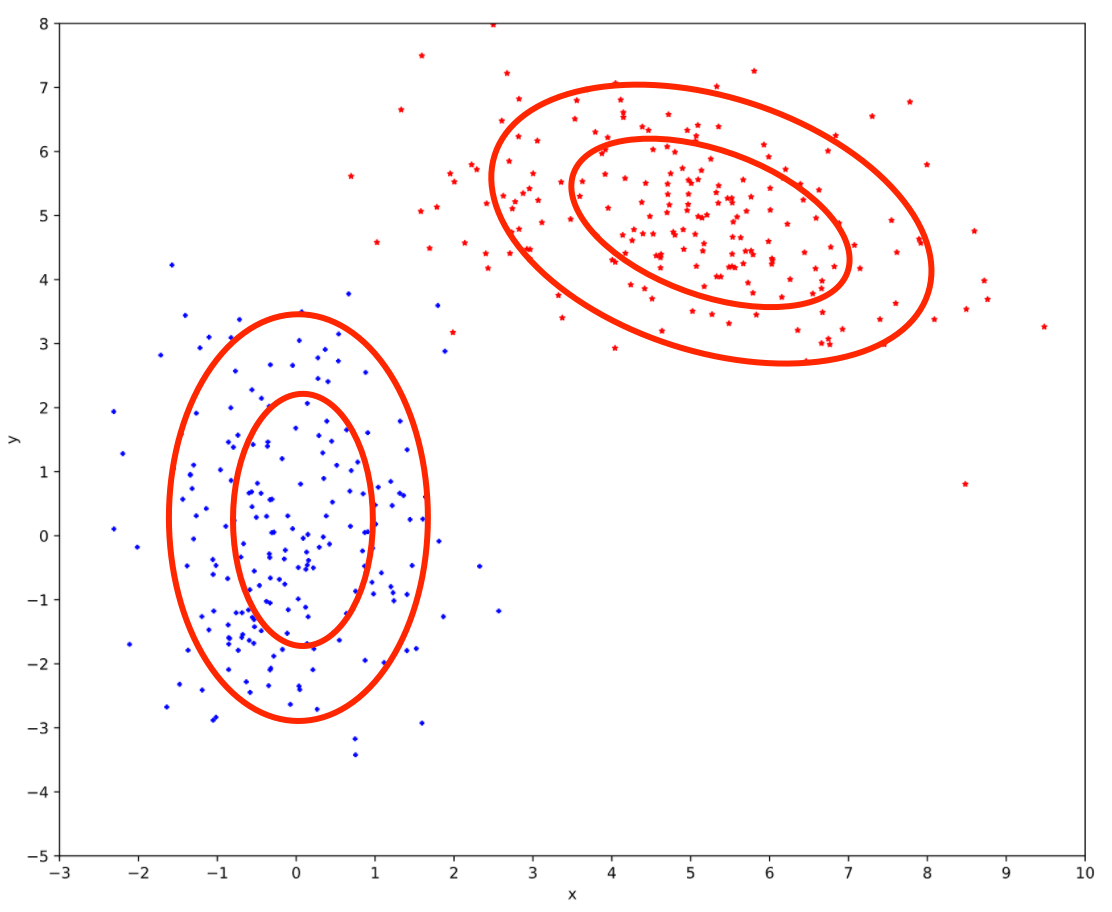
正当单高斯模型抓耳挠腮的时候, 混合高斯模型就大摇大摆地进场了. 它通过求解两个高斯模型, 并通过一定的权重将两个高斯模型融合成一个模型, 即最终的混合高斯模型. 这个混合高斯模型可以产生这样的样本.

更一般化的描述为: 假设混合高斯模型由 $K$ 个高斯模型组成 (即数据包含K个类), 则 GMM 的概率密度函数如下:

$$f(x)=\sum_{k=1}^Kp(k)p(x|k)=\sum_{k=1}^K\pi_kN(x|\mu_k,\small{\Sigma}_k)$$

其中, $p(k)=\pi_k$ 是第 $k$ 个高斯模型的权重, 称作选择第 $k$ 个模型的先验概率, 且满足 $\sum_{k=1}^K\pi_k=1$. 而 $p(x|k)=N(x|\mu_k,\Sigma_k)$ 则是第 $k$ 个高斯模型的概率密度函数, 可以看成选定第 $k$ 个模型之后, 该模型产生 $x$ 的概率.

2.1 Intuition

我们接下来通过几张图片来帮助理解混合高斯模型, 我们先从简单的一维混合高斯模型说起.

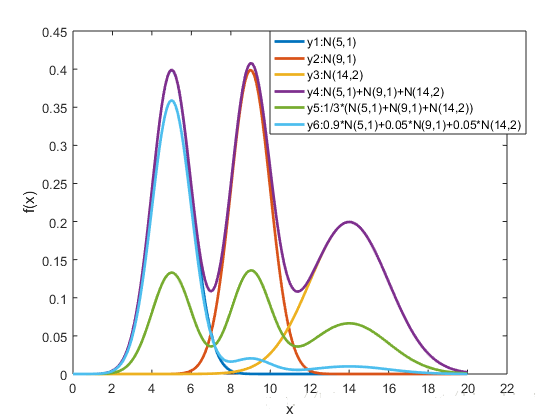
在上图中, $y_1,y_2,y_3$ 分别表示三个一维高斯模型, 他们的参数设定如图例所示. $y_4$ 表示将三个模型的概率密度函数直接相加, 注意的是这并不是一个混合高斯模型, 因为并不满足 $\sum_{k=1}^K\pi_k=1$ 的条件. 而 $y_5$ 和 $y6$ 则分别是由不同的权重对 $y_1,y_2,y_3$ 进行混合所得的模型. 由此可见, 调整权重将极大影响混合模型的概率密度函数曲线. 另一方面也可以直观地理解混合高斯模型可以更好地拟合样本的原因: 它有更复杂更多变的概率密度函数曲线. 理论上, 混合高斯模型的概率密度函数曲线可以是任意形状的非线性函数.

我们接下来再给出一个二维空间 3 个高斯混合模型的例子.

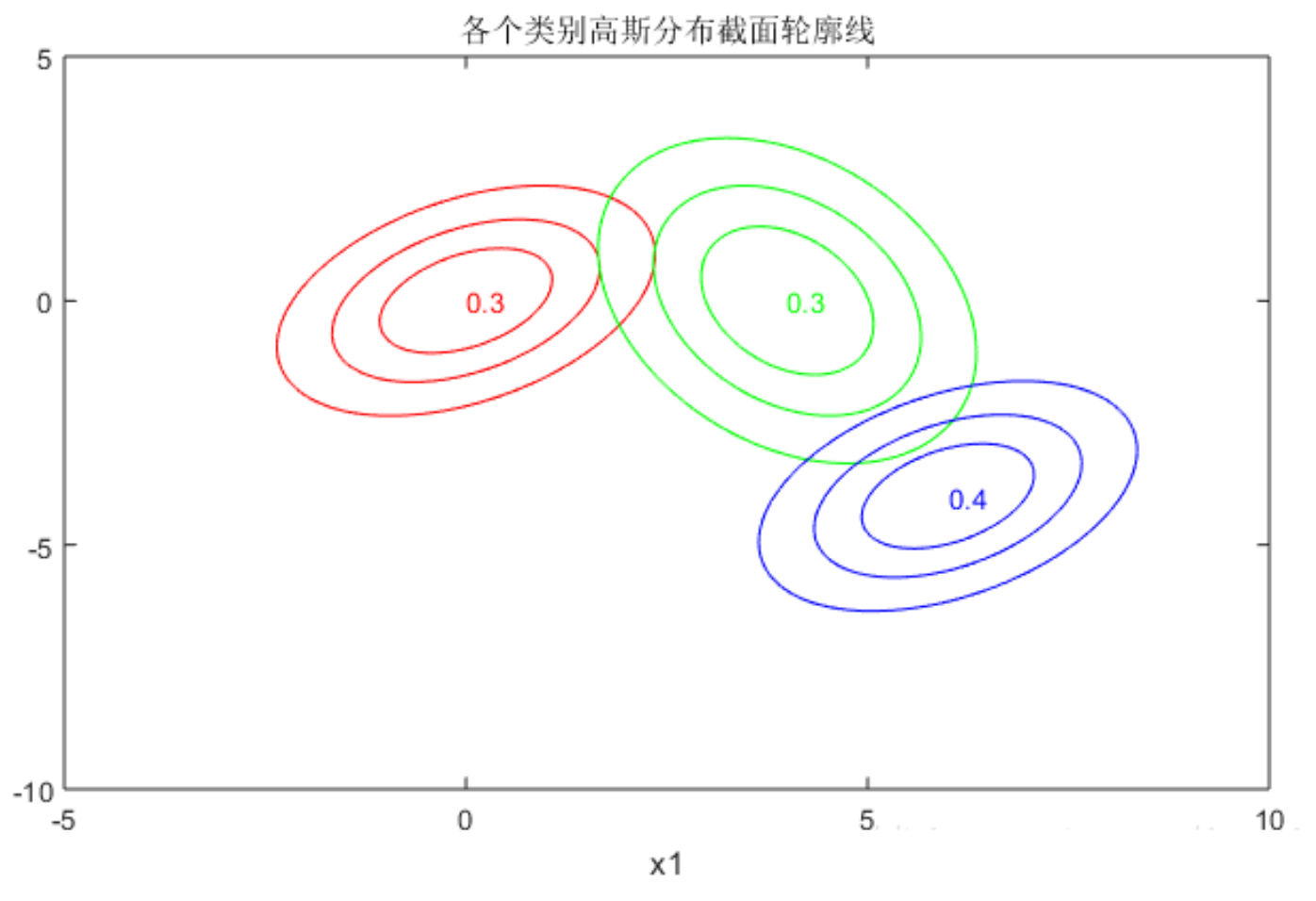
这个图是 3 个高斯模型的截面轮廓图, 图中数字是各个模型组成 GMM 的权重系数. 由截面轮廓图可知3个模型之间存在很多重叠区域. 其实这也正是混合高斯模型所希望的. 因为如果它们之间的重叠区域较少, 那么生成的混合高斯模型一般较为简单, 难以生成较为复杂的样本.

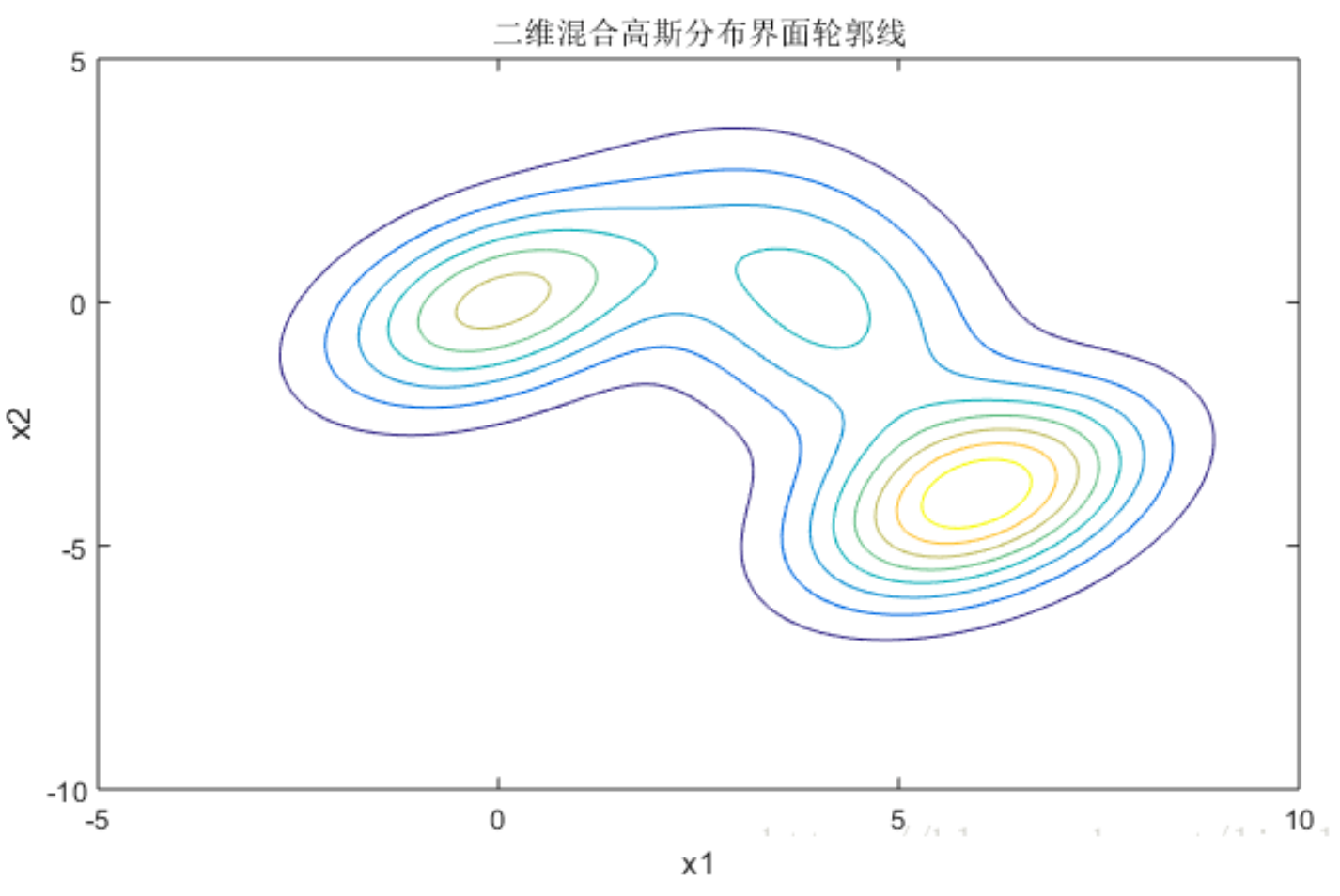
设定好了 3 个高斯模型和它们之间的权重系数之后, 就可以确定二维混合高斯分布的概率密度函数曲面. 我们可以看到, 整个混合高斯分布曲面相对比于单高斯分布曲面已经异常复杂. 实际上, 通过调整混合高斯分布的系数 $(\pi,\mu,\sum)$, 我们可以使得高斯分布概率密度图去拟合任意的三维曲面, 从而采样生成所需的数据样本.

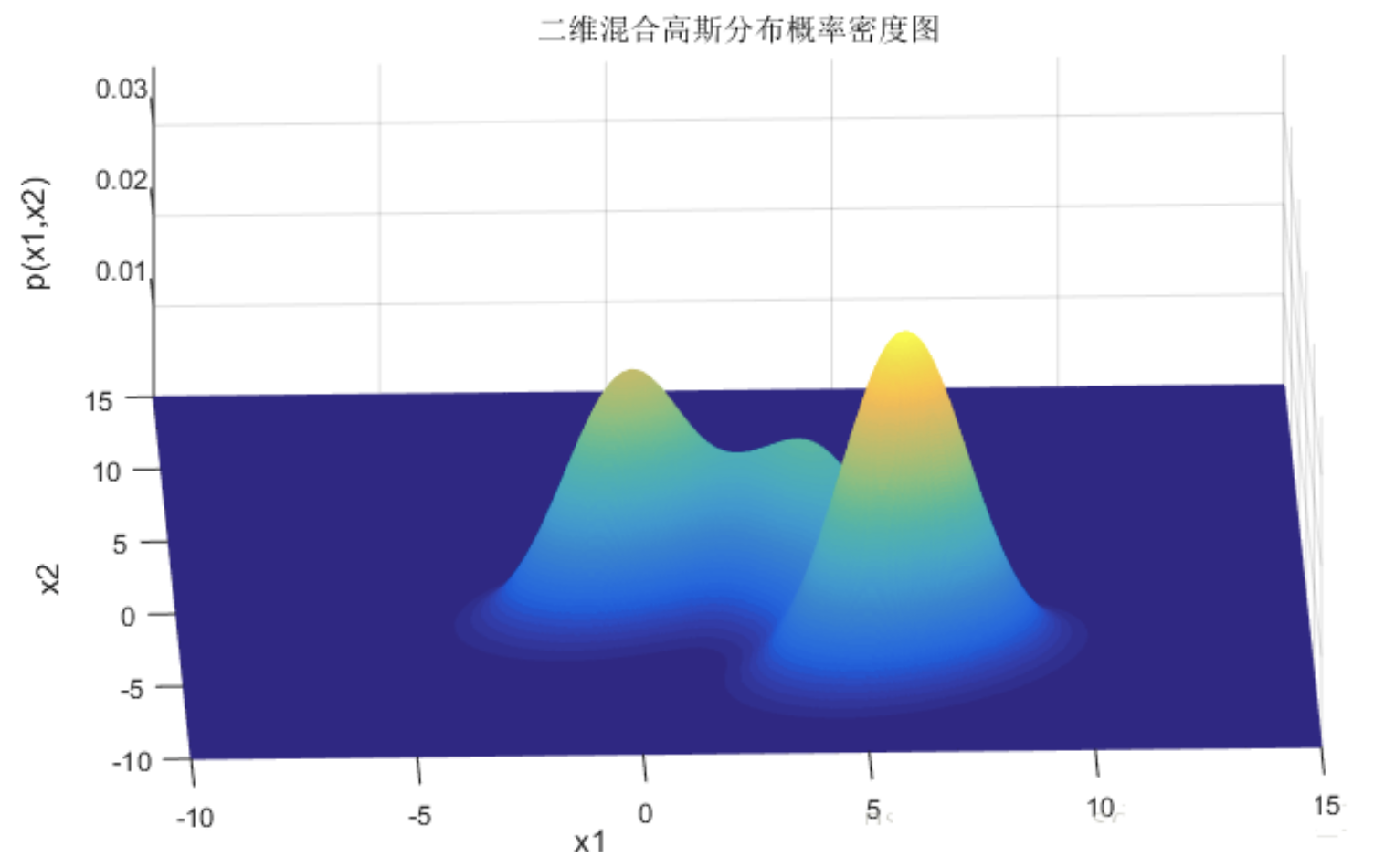
2.2 Parameter Estimation

如果看过我之前讲贝叶斯和逻辑回归的文章, 那么你已经对最大似然估计非常熟悉了. 我们现在也可以用最大似然估计来求解 GMM 模型. 我们首先来回顾一下 GMM 的概率密度函数:

$$f(x)=\sum_{k=1}^Kp(k)p(x|k)=\sum_{k=1}^K\pi_kN(x|\mu_k,\small{\Sigma}_k)$$

我们根据上式不难写出对数似然函数为:

$$\ell(\pi,\mu,\Sigma)=\ln p(X;\pi,\mu,\Sigma)=\sum_{i=1}^N\ln(\sum_{k=1}^K\pi_kN(x_i;\mu_k,\Sigma_k))$$

好了, 然后求导, 令导数为0, 得到模型参数 $\pi,\mu,\Sigma$.

貌似问题已经解决了! 然而仔细观察可以发现, 对数似然函数里面还有求和. 实际上没有办法通过求导的方法来求这个对数似然函数的最大值. 怎么办？

这时候就要要到EM算法求解.

我们接下来看看 EM 算法和 MLE 的不同适用场景:

1. MLE

   已知:

   • 数据分布模型
   • 采样数据

   未知:

   • 数据分布模型参数

2. EM Algorithm

   已知:

   • 各个类的分布模型
   • 采样数据

   未知:

   • 采样数据分别来自哪一类
   • 各个模型的参数

如果我们已经清楚了某个变量服从的高斯分布, 而且通过采样得到了这个变量的样本数据, 想求高斯分布的参数, 这时候极大似然估计可以胜任这个任务.

而如果我们要求解的是一个混合模型, 只知道混合模型中各个类的分布模型 (譬如都是高斯分布) 和对应的采样数据, 而不知道这些采样数据分别来源于哪一类 (隐变量), 那这时候就可以借鉴EM算法. EM算法可以用于解决数据缺失的参数估计问题 (隐变量的存在实际上就是数据缺失问题, 缺失了各个样本来源于哪一类的记录).

3. EM Algorithm

3.1 Intuition

我们先通过一个简单的案例来引入 EM 算法.

假设有 1 枚硬币 A, 这枚硬币正面出现的概率是 $p$. 进行掷硬币试验: 投掷硬币 A, 出现正面记作 1, 出现反面记作 0; 独立地重复 $n$ 次. 这是一个参数为 $p$ 的伯努利分布:

$$p(x)=p^x(1-p)^{1-x}$$

如果给定一个结果序列 $n=10$, 如下:

$$1 \quad 1\quad 0\quad 1\quad 1\quad 1\quad 0\quad 0\quad 1\quad 1$$

$p$ 可以通过极大似然估计得到:

$$p=\frac{\sum_{i=1}^nI(x_i=1)}{n}=\frac{7}{10}$$

现在考虑更复杂的情况, 假设有3枚硬币, 分别记作A, B, C. 这些硬币正面出现的概率分别是 $\pi$, $p$ 和 $q$. 进行如下掷硬币试验: 先掷硬币A, 根据其结果选出硬币B或硬币C, 如果是正面选择硬币B, 如果是反面选择硬币C; 然后掷选出的硬币, 掷硬币的结果, 出现正面记作1, 出现反面记作0; 独立地重复 $n$ 次试验 (这里, $n=10$), 观察结果如下:

$$1 \quad 1\quad 0\quad 0\quad 1\quad 0\quad 1\quad 0\quad 1\quad 1$$

这种情况下, 如果我们知道了如下带有颜色的结果, 红色表示由硬币B掷出, 绿色表示由硬币C掷出, 即我们知道每次硬币A掷出的结果:

$$\color{red}{1} \quad \color{red}{1}\quad \color{green}{0}\quad \color{green}{0}\quad \color{red}{1}\quad \color{green}{0}\quad \color{red}{1}\quad \color{red}{0}\quad \color{green}{1}\quad \color{red}{1}$$

我们可以很容易的估计出参数 $\pi$, $p$ 和 $q$:

$$\pi = \frac{红色的个数}{总个数} \quad p=\frac{红色中1的个数}{红色的个数} \quad q=\frac{绿色中1的个数}{绿色的个数}$$

但是现在的问题是, 我们并不知道每次硬币A掷出的结果, 也就是我们并不能够看到如上的带有颜色的结果, 这时怎么估计参数 $\pi$, $p$ 和 $q$ 呢?

对于这个问题, 按照极大似然估计的思路, 令 $θ=(π,p,q)$, 我们希望求得参数 $\theta$, 使得

$$\theta=\mathop{\arg\max}_\theta p(x;\theta)$$

但是因为此时我们无法观测到掷硬币A的结果, 所以需要引入隐变量 $z$, $z∈{0,1}$, 若 $z=1$ 表示使用硬币B，若 $z=0$ 表示使用硬币C, 因此

$$\begin{equation} \begin{aligned} p(x;\theta)=&\sum_{z}p(x,z;\theta) \\ =&\sum_{z}p(x|z;\theta)p(z;\theta) \\ =& p(x|z=1;\theta)p(z=1;\theta)+p(x|z=0;\theta)p(z=0;\theta) \end{aligned} \end{equation}$$

其中, 我们知道:

$$p(x|z=1;\theta) = p^x(1-p)^{1-x} \\ p(x|z=0;\theta) = q^x(1-q)^{1-x} \\ p(z=1;\theta)=\pi \quad p(z=0;\theta)=1-\pi$$

所以有:

$$p(x;\theta) = {\color{red}{\pi p^x(1-p)^{1-x}}} + \color{green}{(1-\pi)q^x(1-q)^{1-x}}$$

我们用 $\mu$ 表示在给定当前参数 $θ=(π,p,q)$ 情况下, 每个试验结果 $x$ 由硬币B产生的概率, 则

$$\mu=\frac{\pi p^x(1-p)^{1-x}}{\pi p^x(1-p)^{1-x} + (1-\pi)q^x(1-q)^{1-x}}, x\in \{0,1\}$$

给定一个观测到的结果序列 $x=\{x_1,x_2,…,x_N\}$, 则有:

$$\mu_i=\frac{\pi p^{x_i}(1-p)^{1-{x_i}}}{\pi p^{x_i}(1-p)^{1-{x_i}} + (1-\pi)q^{x_i}(1-q)^{1-{x_i}}}$$

至此, 需要发挥一点想象力, 假设我们观察到一个结果为正面的硬币, 现在它不再如之前所述的完全是红色(硬币B产生)和绿色(硬币C产生), 而是有一部分红色(概率是 $\mu_i$), 一部分绿色(概率是 $1-\mu_i$), 如下图所示:

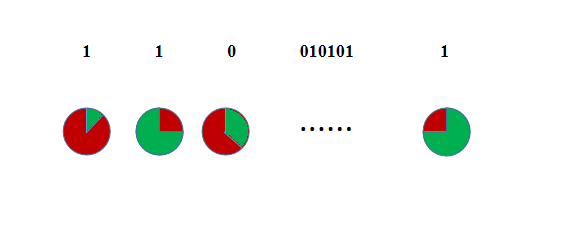
接下来我们就可以根据 $\mu_i$ 重新估计参数 $\theta=(\pi,p,q)$, 注意, 为什么说是重新估计参数, 因为 $\mu_i$ 是根据当时给定参数 $\theta=(\pi,p,q)$ 计算出来的. 根据我们之前初始化参数的方法, 有:

$$\begin{aligned} &\pi=\frac{红色的个数}{总个数}=\frac{\sum_{i=1}^N\mu_i}{N} \\ &p=\frac{红色中1的个数}{红色的个数}=\frac{\sum_{i=1}^N\mu_ix_i}{\sum_{i=1}^N\mu_i} \\ &q=\frac{绿色中1的个数}{绿色的个数}=\frac{\sum_{i=1}^N(1-\mu_i)x_i}{\sum_{i=1}^N(1-\mu_i)} \end{aligned}$$

好了, 通过不断的重复上述步骤, 直到参数 $\theta=(\pi,p,q)$ 不再变化, 我们就得到了参数的最优估计. 至此, 我们直观地解释了 EM 算法:

• E Step:

  E 是 Expectation, 也就是期望. 代入到我们问题中, 也就是求在当前参数 $\theta$ 下, 计算 $\mu$ 的期望.

  Note: 初始化时, 我们可以根据数据先验分布去计算 $\theta$.

• M Step:

  使用通过 E Step 得到的 $\mu$ 根据最大似然估计来重新计算 $\theta$.

重复上述步骤, 直至收敛.

3.2 Math Trick

给定给定训练样本是 $\{x^{(1)},x^{(2)},…,x^{(m)}\}$, 样本独立同分布, 我们想要找到每个样例隐含类别 $z$, 能使得 $p(x,z)$ 最大. $p(x,z)$ 的最大似然估计如下:

$$\begin{aligned} \ell(\theta)=&\sum_{i=1}^m \log p(x;\theta)\\ =&\sum_{i=1}^m\log \sum_{z}p(x,z;\theta) \end{aligned}$$

第一步是对极大似然取对数; 第二步是对每个样例的每个可能类别 $z$ 求联合分布概率和. 但是直接求 $\theta$ 一般比较困难, 因为有隐藏变量 $z$ 的存在, 但是一般确定了 $z$ 后, 求解就容易了.

EM是一种解决存在隐含变量优化问题的有效方法. 既然不能直接最大化 $\ell(\theta)$, 我们可以不断地建立 $\ell(\theta)$ 的下界 (E Step), 然后优化下界 (M Step). 这句话比较抽象, 看下面的.

对每个样例 $i$, 让 $Q_i$ 表示该样例隐含变量 $z$ 的某种分布, $Q_i$ 满足的条件是 $\sum_zQ_i(z)=1$, $Q_i(z)\ge0$. （如果 $z$ 是连续性的, 那么 $Q_i(z)$ 是概率密度函数, 需要将求和符号换做积分符号). 比如要将班上的学生聚类, 假设隐藏变量 $z$ 是身高, 那么就是连续的高斯分布. 如果按照隐藏变量 $z$ 是性别, 那就是伯努利分布了.

可以由前面阐述的内容得到下面的公式:

$$\begin{aligned} \sum_{i}\log p(x^{(i)};\theta) &= \sum_{i}\log \sum_{z^{(i)}}p(x^{(i)},z^{(i)};\theta) \\ &= \sum_{i}\log \sum_{z^{(i)}} Q_i(z^{(i)}) \cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \\ &\ge \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log \cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \end{aligned} \tag{1}$$

Jensen 不等式:

若 $f(x)$ 为凸函数, 那么有:

$$E(f(x))\ge f(E(x))$$

若 f(x) 为凹函数, 那么正好相反:

$$E(f(x))\le f(E(x))$$

此处推导利用 Jensen 不等式, 考虑 $\log(x)$ 是凹函数, 那么有

$$E(\log(x))\le \log(E(x))$$

而这里的

$$\log \sum_{z^{(i)}} Q_i(z^{(i)}) \cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

可以看成是 $\cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$ 的期望, 因此我们可以根据 Jessen 不等式, 推导出不等关系:

$$f\bigg(E_{z^{(i)\sim Q_i}}\bigg[\cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\bigg]\bigg) \ge E_{z^{(i)\sim Q_i}}\bigg[f\bigg(\cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\bigg)\bigg]$$

因此, 式 (1) 是完全成立的, 而且这个过程可以看作是对 $\ell(\theta)$ 求下界函数. 现在, 我们将式 (1) 写成: 对数似然函数 $\ell(\theta)\ge J(Q,\theta)$:

$$J(Q,\theta)=\ge \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log \cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

显然, $J(Q,\theta)$ 是容易通过求导数, 然后求得极值. 但是由于是不等式, 所以 $J(Q,\theta)$ 的极大值并不是 $\ell(\theta)$ 极大值, 而我们想得到的是 $\ell(\theta)$ 的极大值, 那怎么办?

我们可以通过不断的最大化这个下界 $J$, 来使得 $\ell(\theta)$ 不断提高, 最终达到它的最大值, 如下图所示:

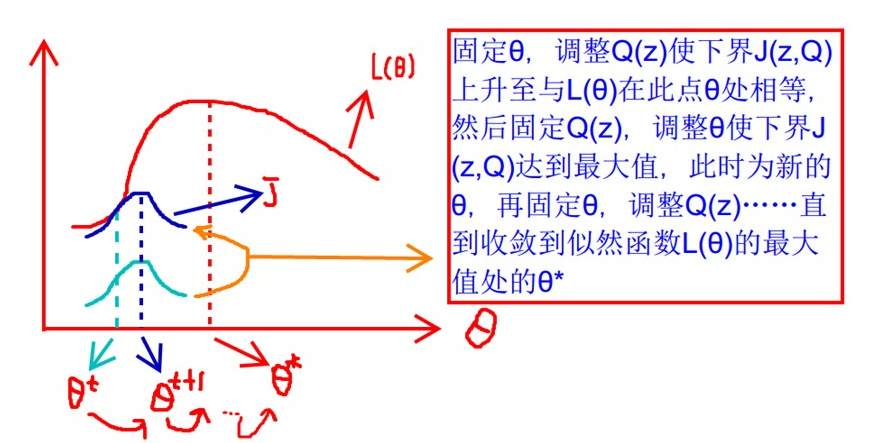
对于 $Q_i$ 的选择, 有多种可能, 那么哪种更好呢? 假设 $\theta$ 已经给定, 即 $θ$ 已经固定, 那么 $ℓ(θ)$ 的值就决定于 $Q_i(z^{(i)})$ 和 $p(x^{(i)},z^{(i)})$ 了. 我们可以通过调整这两个概率使下界 $J(Q,θ)$ 不断上升, 以逼近 $ℓ(θ)$ 的真实值, 那么什么时候算是调整好了呢? 当不等式变成等式时, 说明我们调整后的概率值能够等价于 $\ell(\theta)$ 了 (浅蓝色曲线到蓝色曲线). 然后固定 $Q(z)$, 调整 $\theta$ 使下界 $J(Q,θ)$ 达到最大值 ( $θ_t$ 到 $θ_{t+1}$), 重复上述过程直至收敛到对数似然函数 $ℓ(θ)$ 的极大值处 $\theta^{*}$.

按照这个思路, 我们要找到等式成立的条件. 根据Jensen不等式, 要想等式成立, 需要让随机变量变成常数值, 这里得到:

$$\cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = c$$

取等条件的本质: https://zhuanlan.zhihu.com/p/338571213

其中, $c$ 为常数, 不依赖于 $z_{(i)}$. 对此式子做进一步推导, 我们知道 $\sum_zQ_i(z^{(i)})=1$, 那么也就有 $\sum_zp(x^{(i)},z^{(i)};\theta)=c$, 那么就有了下式:

$$\begin{aligned} Q_i(z^{(i)}) &= \cfrac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z}p(x^{(i)},z^{(i)};\theta)} \\ & = \cfrac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} \\ &= p(z^{(i)}|x^{(i)};\theta) \end{aligned}$$

至此, 我们推出了在固定其他参数 $\theta$ 后, $Q_i(z^{(i)})$ 的计算公式就是后验概率, 解决了 $Q_i(z^{(i)})$ 如何选择的问题. 这一步就是 $E$ 步, 建立 $ℓ(θ)$ 的下界. 接下来的 $M$ 步, 就是在给定 $Q_i(z^{(i)})$ 后, 调整 $θ$, 极大化 $ℓ(θ)$ 的下界 (在固定 $Q_i(z^{(i)})$后, 下界还可以调整的更大). 那么一般的EM算法的步骤如下:

循环重复直至算法收敛:

（$E$ 步） 对于每一个样例 $i$, 计算:

$$Q_i(z^{(i)}) := p(z^{(i)}|x^{(i)};\theta)$$

（$M$ 步） 计算:

$$\theta := arg \smash{\max_\theta} \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \log \cfrac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$

那么, 究竟怎么确保 EM 收敛? 我们假定 $\theta^{(t)}$ 和 $\theta^{(t+1)}$ 是 EM 的第 $t$ 次和 $t + 1$ 次迭代后的结果. 如果我们证明了 $\ell(\theta^{(t)}) \le \ell(\theta^{(t+1)})$, 也就是说极大似然估计单调增加, 那么最终我们会得到极大似然估计的最大值. 下面来证明, 选定 $\theta^{(t)}$ 后, 我们得到 $E$ 步:

$$Q_i^{(t)}(z^{(i)}) := p(z^{(i)}|x^{(i)};\theta^{(t)})$$

这一步保证了在给定 $\theta^{(t)}$ 时, Jensen不等式中的等式成立, 也就是:

$$\ell(\theta^{(t)})=\sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) log \cfrac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})}$$

然后进行 M 步, 固定 $Q_i^{(t)}(z^{(i)})$, 并将 $\theta^{(t)}$ 视作变量, 对上面的 $\theta^{(t)}$ 求导后, 得到 $\theta^{(t+1)}$, 这样经过一些推导会有以下式子成立:

$$\begin{aligned} \ell{(\theta^{(t+1)})} &\ge \sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \cfrac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \\ &\ge \sum_{i} \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \cfrac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \\ &= \ell(\theta^{(t)}) \end{aligned}$$

解释上式第一步, 得到 $θ_{(t+1)}$ 时, 只有最大化 $ℓ(θ^{(t)})$, 也就是 $ℓ(θ^{(t+1)})$ 的下界, 而没有使等式成立, 等式成立只有在固定 $θ$, 并按 $E$ 步得到 $Q_i^{(t+1)}$ 时才能成立.

这样就证明了 $ℓ(θ)$ 会单调增加. 一种收敛方法是 $ℓ(θ)$ 不再变化, 还有一种就是变化幅度很小.

3.3 Solving GMM

[To be done]