贝叶斯统计之美

贝叶斯估计, 最大似然估计(MLE), 最大后验概率估计(MAP) 这几个概念在机器学习和深度学习中经常碰到, 读文章的时候还感觉挺明白, 但独立思考时经常会傻傻分不清楚, 因此希望通过本文对其进行总结.

1. Fundamentals

1.1 概率与统计

下面的一段话引自LarrB Wasserman的《All of Statistics》, 对概率和统计推断的研究内容进行了描述:

The basic problem that we study in in probability is:
Given a data generating process, what are the properties of the outcomes?

The basic problem of statistical inference is the inverse of probability:
Given the outcomes, what can we say about the process that generated the data?

1.2 描述和推断统计

描述统计是对数据的一种概括:

描述统计是罗列所有数据, 然后选择一些特征量 (例如均值、方差、中位数、四分中位数等) 对总体数据进行描述.

推断统计是一种对数据的推测:

推断统计无法获取所有数据, 只能得到部分数据, 然后根据得到的数据推测总体数据的情况.

1.3 联合和边缘概率

假设有随机变量 $A$ 和 $B$, 此时 $P(A=a,B=b)$ 用于表示 $A=a$ 且 $B=b$ 同时发生的概率. 这类包含多个条件且所有条件同时成立的概率称为联合概率. 请注意, 联合概率并不是其中某个条件成立的概率, 而是所有条件同时成立的概率. 与之对应地, $P(A=a)$ 或 $P(B=b)$ 这类仅与单个随机变量有关的概率称为边缘概率.

1.4 条件概率

条件概率表示在条件 $B=b$ 成立的情况下, $A=a$ 的概率，记作 $P(A=a|B=b)$, 或者说条件概率是指事件$A=a$ 在另外一个事件 $B=b$ 已经发生条件下的发生概率. 为了简洁表示, 后面省略a, b.

联合概率, 边缘概率, 条件概率的关系如下:

$$P(A|B)=\frac{P(A,B)}{P(B)}$$

转换为乘法形式:

$$P(A,B)=P(B)\times P(A|B)=P(A)\times P(B|A)$$

1.5 全概率公式

如果事件 $A_1,A_2,A_3,…,A_n$ 构成一个完备事件组, 即这些事件两两互斥, 其和为全集, 则有:

$$P(B)=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+...+P(B|A_n)P(A_n)=\sum_{i=1}^nP(B|A_i)P(A_i)$$

上面的公式称为全概率公式, 全概率公式是对复杂事件AA的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题.

1.6 贝叶斯公式

由条件概率的乘法形式可得:

$$P(A|B)=\frac{P(B|A)}{P(B)}P(A)$$

上面的式子称为贝叶斯公式, 也叫做贝叶斯定理或贝叶斯法则. 在贝叶斯定理中, 每个名词都有约定俗成的名称:

• $P(A|B)$ 是已知 $B$ 发生后 $A$ 的条件概率, 也由于得自 $B$ 的取值而被称为 $A$ 的后验概率, 表示==事件 $B$ 发生后, 事件 $A$ 发生的置信度.==
• $P(A)$ 是 $A$ 的先验概率或边缘概率, 表示==事件 $A$ 发生的置信度.==
• $P(B|A)$ 是已知 $A$ 发生后 $B$ 的条件概率, 也由于得自 $A$ 的取值而被称作 $B$ 的后验概率, 也被称作似然函数.
• $P(B)$ 是 $B$ 的先验概率或边缘概率, 称为标准化常量.
• $\frac{P(B|A)}{P(B)}$ 称为标准似然比, 表示==事件 $B$ 为事件 $A$ 发生提供的支持程度.==

因此贝叶斯公式可表示为: 后验概率=似然函数*先验概率/标准化常量=标准似然比*先验概率. 根据标准似然比的大小, 可分为下面三种情况:

• 如果标准似然比 $>1$, 则先验概率 $P(A)$ 得到增强, 事件 $B$ 的发生会增大事件 $A$ 发生的可能性;
• 如果标准似然比 $=1$. 则先验概率 $P(A)$ 保持不变, 事件 $B$ 的发生不影响事件 $A$ 发生的可能性;
• 如果标准似然比 $<1$, 则先验概率 $P(A)$ 得到削弱, 事件 $B$ 的发生会降低事件 $A$ 发生的可能性.

由全概率公式, 贝叶斯法则可得:

$$P(A_i|B)=\frac{P(B|A_i)P(A_i)}{P(B)}=\frac{P(B|A_i)P(A_i)}{\sum_{j=1}^nP(B|A_j)P(A_j)}$$

1.7 似然与概率

在英文中, 似然（likelihood）和概率（probability）是同义词, 都指事件发生的可能性. 但在统计中, 似然与概率是不同的东西.

• 概率是已知参数, 对结果可能性的预测.
• 似然是已知结果, 对参数是某个值的可能性预测.

对于函数 $P(x|\theta)$, 从不同的观测角度来看可以分为以下两种情况:

• 如果 $\theta$ 已知且保持不变, $x$ 是变量, 则称 $P(x|\theta)$ 为概率函数, 表示不同 $x$ 出现的概率.
• 如果 $x$ 已知且保持不变, $\theta$ 是变量, 则称 $P(x|\theta)$ 为似然函数, 表示不同 $\theta$ 下, $x$ 出现的概率, 也记作 $L(\theta|x)$ 或 $L(x;\theta)$.

注：注意似然函数的不同写法.

1.8 频率学派和贝叶斯学派

注：频率学派与贝叶斯学派只是解决问题的角度不同.

频率学派与贝叶斯学派探讨「不确定性」这件事时的出发点与立足点不同.

• 频率主义学派 (Frequentist)

  频率学派从「自然」角度出发, 试图直接为「事件」本身建模, 即事件 $A$ 在独立重复试验中发生的频率趋于极限 $p$, 那么这个极限就是该事件的概率.

  频率学派的代表是最大似然估计 (MLE).

• 贝叶斯学派 (Bayesian)

  贝叶斯学派并不从试图刻画「事件」本身, 而从「观察者」角度出发. 贝叶斯学派并不试图说「事件本身是随机的」, 或者「世界的本体带有某种随机性」, 这套理论根本不言说关于「世界本体」的东西, 而只是从「观察者知识不完备」这一出发点开始, 构造一套在贝叶斯概率论的框架下可以对不确定知识做出推断的方法.

  贝叶斯学派的代表是最大后验概率估计 (MAP).

2. MLE & MAP

以抛硬币为例, 假设我们有一枚硬币, 现在要估计其正面朝上的概率 $\theta$. 为了对 $\theta$ 进行估计, 我们进行了10次实验 (独立同分布, i.i.d.), 这组实验记为 $X=x_1,x_2,…,x_{10}$, 其中正面朝上的次数为6次, 反面朝上的次数为4次, 结果为$(1,0,1,1,0,0,0,1,1,1)$.

2.1 MLE

最大似然估计, 英文为 Maximum Likelihood Estimation, 简写为MLE, 也叫极大似然估计, 是用来估计概率模型参数的一种方法. 最大似然估计的思想是使得观测数据（样本）发生概率最大的参数就是最好的参数.

对一个独立同分布的样本集来说, 总体的似然就是每个样本似然的乘积. 针对抛硬币的问题, 似然函数可写作:

$$L(X,\theta)=\prod_{i=0}^nP(x_i|\theta)=\theta^6(1-\theta)^4$$

根据最大似然估计, 使 $L(X;\theta)$ 取得最大值的 $\theta$ 即为估计结果, 令 $L(X;\theta)’=0$ 可得 $\hat{\theta}=0.6$. 似然函数图如下:

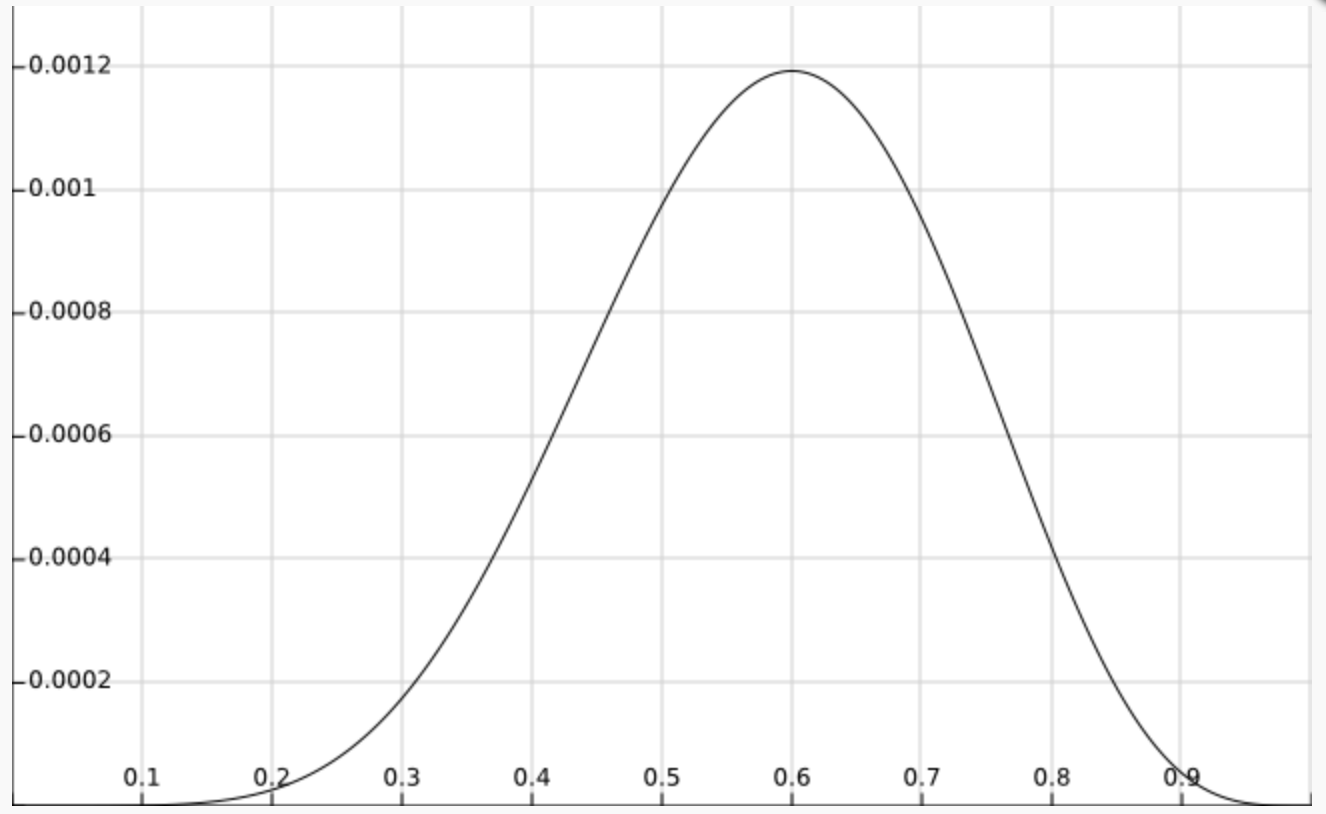
由于总体的似然就是每个样本似然的乘积, 为了求解方便 (防止下溢), 我们通常会将似然函数转成对数似然函数, 然后再求解. 可以转成对数似然函数的主要原因是对数函数并不影响函数的凹凸性. 因此上式可变为:

$$\ln L(X;\theta)=\ln\prod_{i=0}^nP(x_i|\theta)=\sum_{i=0}^n\ln P(x_i|\theta)=6\ln(\theta)+4\ln(1-\theta)$$

令 $(\ln L(X;\theta))’=0$, 可得 $\hat{\theta}=0.6$.

2.2 MAP

最大后验概率估计, 英文为 Maximum A Posteriori Estimation, 简写为MAP. 回到抛硬币的问题, 最大似然估计认为使似然函数 $P(X|θ)$ 最大的参数 $θ$ 即为最好的 $θ$, 此时最大似然估计是将 $θ$ 看作固定的值, 只是其值未知.

最大后验概率分布认为 $θ$ 是一个随机变量, 即 $θ$ 具有某种概率分布, 称为先验分布, 求解时除了要考虑似然函数 $P(X|θ)$ 之外, 还要考虑 $θ$ 的先验分布 $P(θ)$, 因此其认为使 $P(X|θ)P(θ)$ 取最大值的 $θ$ 就是最好的 $θ$. 此时要最大化的函数变为 $P(X|θ)P(θ)$, 由于 $X$ 的后验分布 $P(X)$ 是固定的, 因此最大化函数可变为 $\frac{P(X|\theta)P(\theta)}{P(X)}$, 根据贝叶斯法则, 要最大化的函数 $\frac{P(X|\theta)P(\theta)}{P(X)}=P(\theta|X)$, 因此要最大化的函数是 $P(\theta|X)$, 而 $P(\theta|X)$ 是 $\theta$ 的后验概率.

最大后验概率估计可以看作是正则化的最大似然估计, 当然机器学习或深度学习中的正则项通常是加法, 而在最大后验概率估计中采用的是乘法, $P(\theta)$ 是正则项. 在最大似然估计中，由于认为 $θ$ 是固定的, 因为 $P(\theta)=1$.

最大后验概率估计的公式表示:

$$\mathop{\arg\max}\limits_{\theta}P(\theta|X)=\mathop{\arg\max}\limits_{\theta}\frac{P(X|\theta)P(\theta)}{P(X)}\varpropto\mathop{\arg\max}\limits_{\theta}P(X|\theta)P(\theta)$$

在抛硬币的例子中, 通常认为 $θ=0.5$ 的可能性最大, 因此我们用均值为 $0.5$, 方差为 $0.1$ 的高斯分布来描述 $θ$ 的先验分布, 当然也可以使用其它的分布来描述 $θ$ 的先验分布. $θ$ 的先验分布为:

$$\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(\theta-\mu)^2}{2\sigma^2}}=\frac{1}{10\sqrt{2\pi}}e^{-50(\theta-0.5)^2}$$

先验分布的函数图如下:

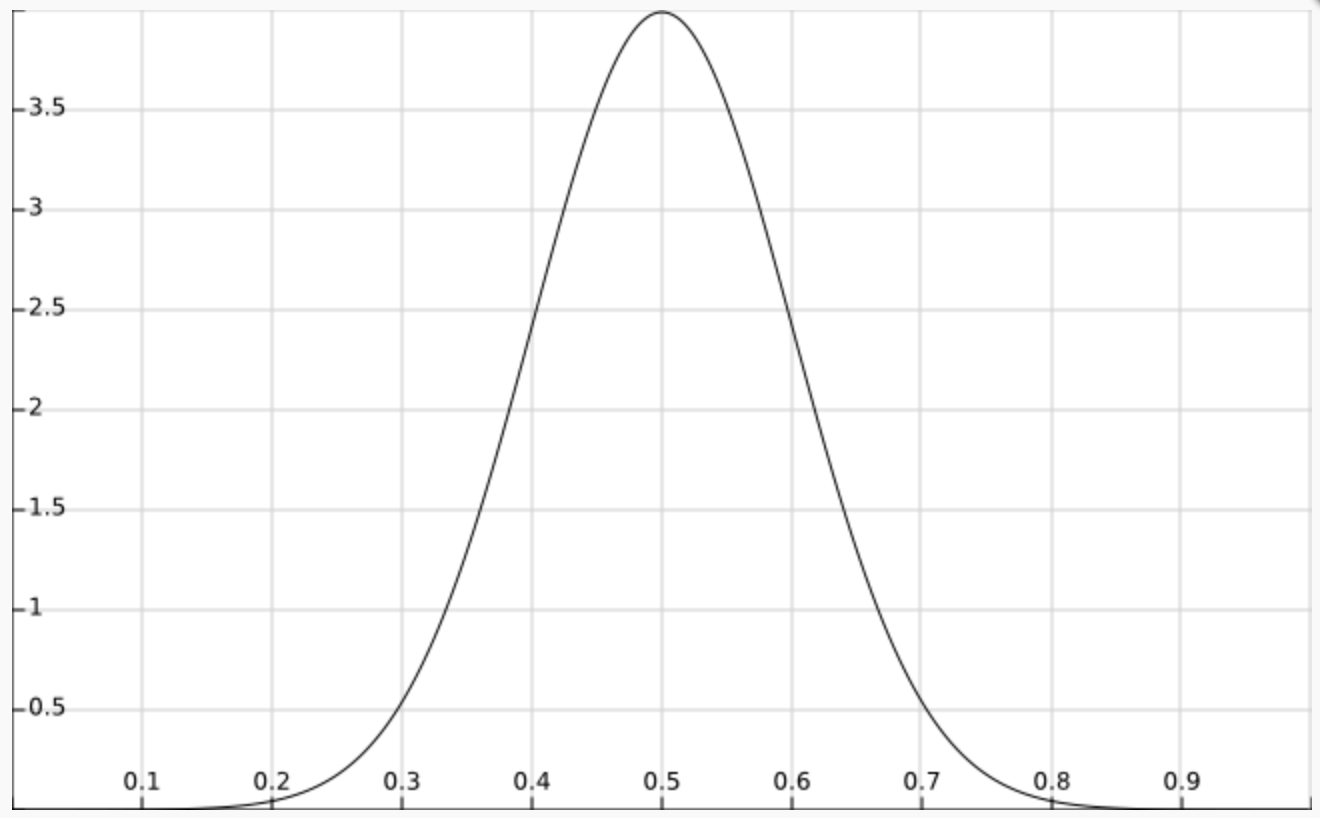
在最大似然估计中，已知似然函数为 $P(X|θ)$, 因此:

$$P(X|\theta)P(\theta)=\theta^6(1-\theta)^4\frac{1}{10\sqrt{2\pi}}e^{-50(\theta-0.5)^2}$$

转换为对数函数求导后可以得到: $\hat{\theta}=0.529$.

$P(X|\theta)P(\theta)$ 的函数图像如下, 基本符合 $\theta$ 的估计值 $\hat{\theta}$:

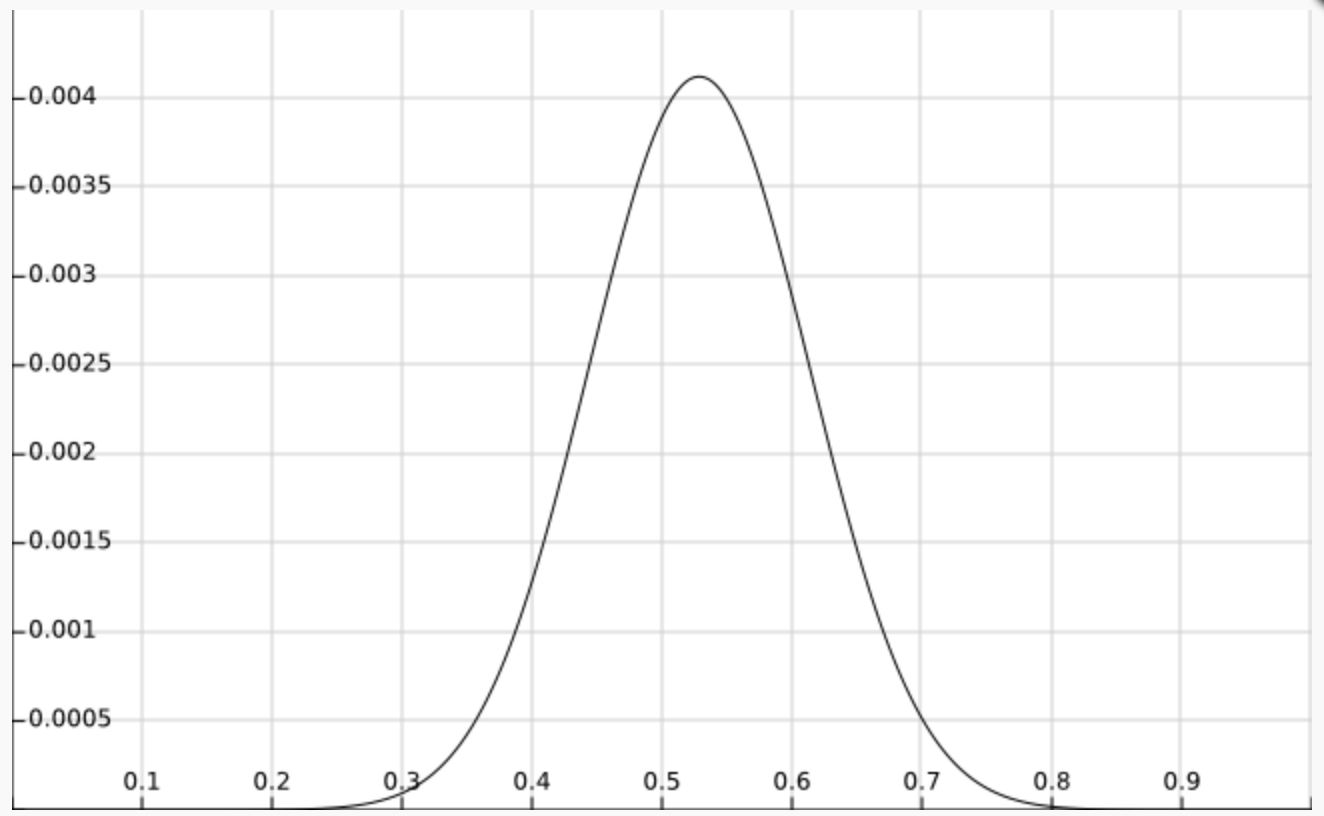
如果我们用均值为 $0.6$, 方差为 $0.1$ 的高斯分布来描述 $\theta$ 的先验分布, 则 $\hat{\theta}=0.6$. 由此可见, 在最大后验概率估计中, $\theta$ 的估计值与 $\theta$ 的先验分布有很大的关系. 这也说明一个合理的先验概率假设是非常重要的, 如果先验分布假设错误, 则会导致估计的参数值偏离实际的参数值.

2.3 Bayesian Estimation

贝叶斯估计是最大后验估计的进一步扩展, 贝叶斯估计同样假定 $\theta$ 是一个随机变量, 但贝叶斯估计并不是直接估计出 $θ$ 的某个特定值, 而是估计 $θ$ 的分布, 这是贝叶斯估计与最大后验概率估计不同的地方. 在贝叶斯估计中, 先验分布 $P(X)$ 是不可忽略的. 回到抛硬币的例子中, 在已知 $X$ 的情况下, 描述 $θ$ 的分布即描述 $P(θ|X)$, $P(θ|X)$ 是一种后验分布.

如果后验分布的范围较窄, 则估计值的准确度相对较高. 反之, 如果后验分布的范围较广, 则估计值的准确度就较低.

贝叶斯公式:

$$P(\theta|X)=\frac{P(X|\theta)P(\theta)}{P(X)}$$

在连续型随机变量中, 由于 $P(X)=\int_{\theta}P(X|\theta)P(\theta)d\theta$, 因此贝叶斯公式变为:

$$P(\theta|X)=\frac{P(X|\theta)P(\theta)}{\int_{\theta}P(X|\theta)P(\theta)d\theta}$$

从上面的公式中可以看出, 贝叶斯估计的求解非常复杂, 因此选择合适的先验分布就非常重要. 对于这个抛硬币的例子来说, 如果使用共轭先验分布, 就可以更好的解决这个问题. 二项分布参数的共轭先验是Beta分布, 由于 $θ$ 的似然函数服从二项分布, 因此在贝叶斯估计中, 假设 $\theta$ 的先验分布服从 $P(\theta)∼Beta(\alpha,\beta)$, Beta分布的概率密度公式为:

$$f(x;\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$

因此, 贝叶斯公式可写作:

$$\begin{aligned} P(\theta|X)&=\frac {P(X|\theta)P(\theta)} {\int_{\Theta}P(X|\theta)P(\theta)d\theta} \\ &=\frac {\theta^6(1-\theta)^4 \frac {\theta^{\alpha-1}(1-\theta)^{\beta-1}} {B(\alpha,\beta)} } {\int_{\Theta}\theta^6(1-\theta)^4 \frac {\theta^{\alpha-1}(1-\theta)^{\beta-1}} {B(\alpha,\beta)}d\theta} \\&=\frac {\theta^{\alpha+6-1}(1-\theta)^{\beta+4-1}} {\int_{\Theta}\theta^{\alpha+6-1}(1-\theta)^{\beta+4-1}d\theta} \\ &=\frac {\theta^{\alpha+6-1}(1-\theta)^{\beta+4-1}} {B(\alpha+6-1,\beta+4-1)} \\ &=Beta(\theta|\alpha+6-1,\beta+4-1) \\&=Beta(\theta|\alpha+6,\beta+4)\end{aligned}$$

从上面的公式可以看出, $P(\theta|X) \sim Beta(\theta|\alpha+6,\beta+4)$. 其中 $B$ 函数, 也称 $Beta$ 函数, 是一个标准化常量, 用来使整个概率的积分为1. $Beta(θ|α+6,β+4)$ 就是贝叶斯估计的结果.

如果使用贝叶斯估计得到的 $θ$ 分布存在一个有限均值, 则可以用后验分布的期望作为 $θ$ 的估计值. 假设$α=3,β=3$, 在这种情况下, 先验分布会在 $0.5$ 处取得最大值, 则 $P(θ|X)∼Beta(θ|9,7)$, 曲线如下图:

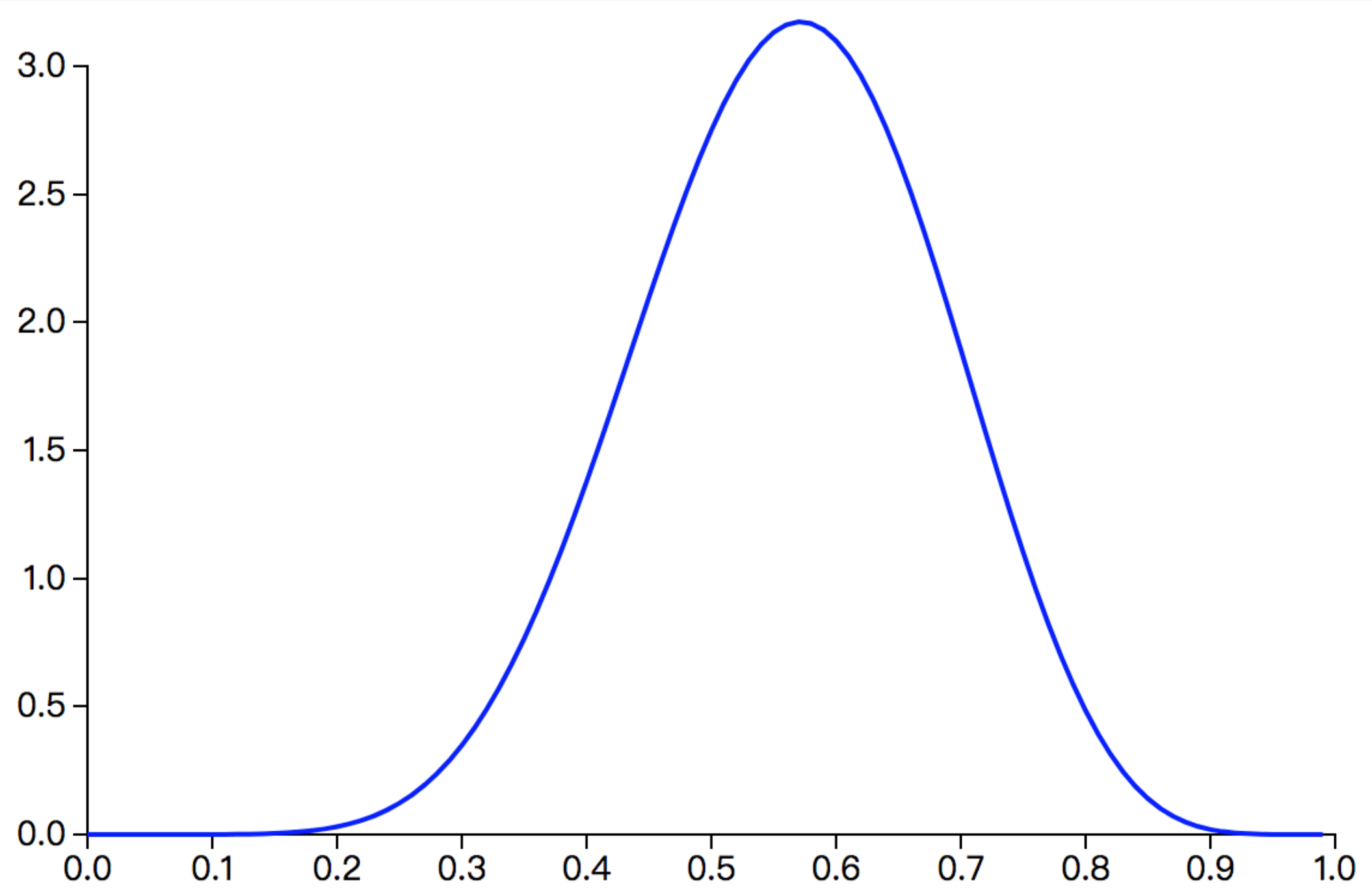
从上图可以看出, 在 $α=3,β=3$ 的情况下，$θ$ 的估计值应该在0.6附近. 根据Beta分布的数学期望公式 $E(\theta)=\frac{\alpha}{\alpha+\beta}$ 可得:

$$\hat{\theta}=\int_{\Theta} \theta P(\theta|X)d\theta=E(\theta)=\frac {\alpha} {\alpha+\beta}=\frac {9} {9+7}=0.5625$$

贝叶斯估计的求解步骤：

• 确定参数的似然函数
• 确定参数的先验分布，应是后验分布的共轭先验
• 确定参数的后验分布函数
• 根据贝叶斯公式求解参数的后验分布

3. Discriminative & Generative Model

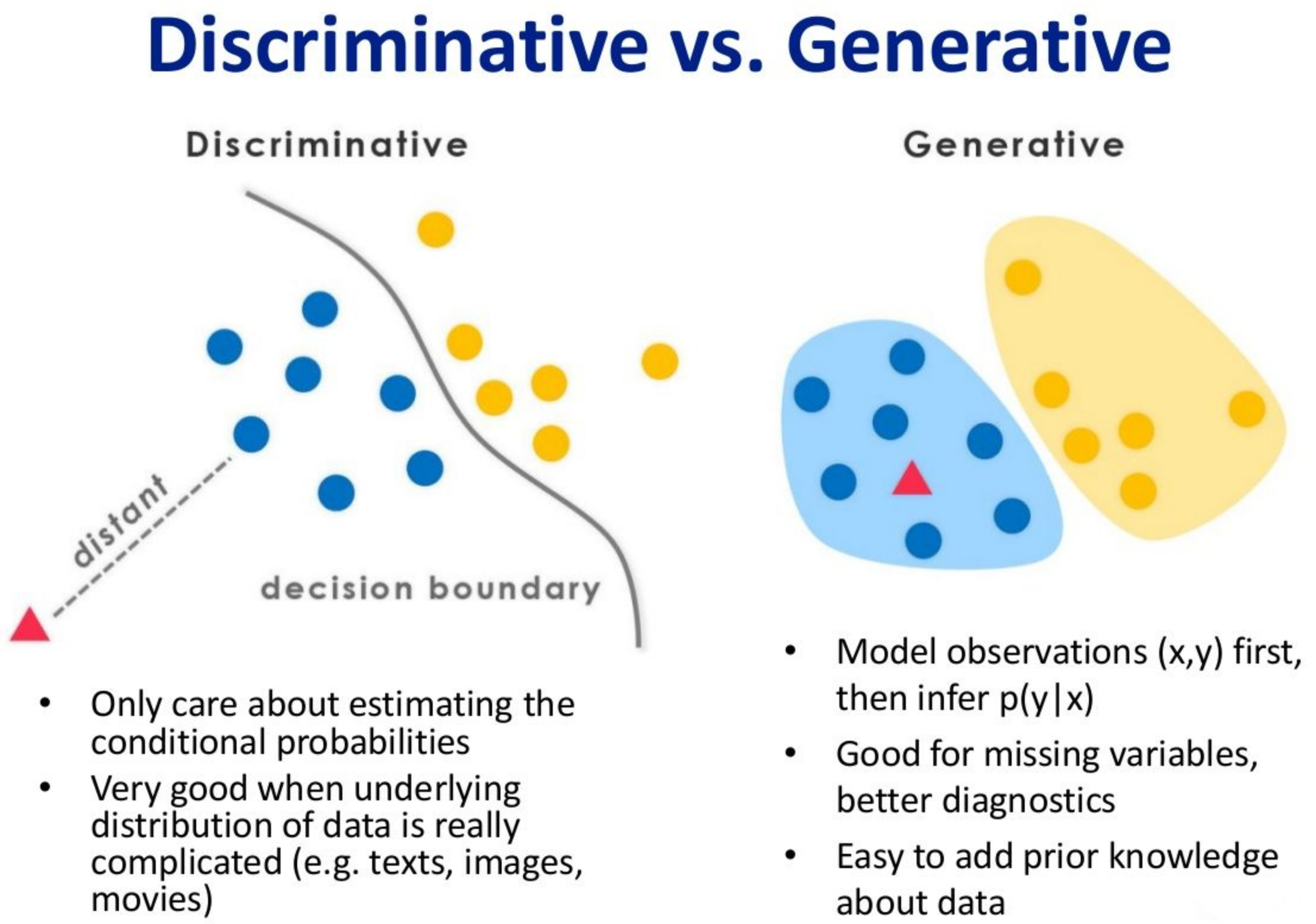
我们先给出最直观的理解:

• 判别式模型

  要确定一个图片是猫还是狗, 用判别模型的方法就是根据数据集 $X$ 训练模, 然后把新的图片输入到模型中, 模型给出这个图片是每个类别的概率.

• 生成式模型

  生成式模型是对原始数据集X和其标签 $Y$ 建模, 生成其联合概率. 然后将新的图片放入是否是猫的模型中, 看概率是多少. 然后将新的图片放入是否是狗的模型中, 看概率是多少.

数据要求: 生成模型需要的数据量比较大, 能够较好地估计概率密度; 而判别模型对数据样本量的要求没有那么多.

3.1 Discriminative Model

对于判别式模型来说求得 $P(Y|X)$, 对未见示例 $X$, 根据 $P(Y|X)$ 可以求得标记 $Y$, 即可以直接判别出来, 如上图的左边所示, 实际是就是直接得到了判别边界.

典型的判别模型包括: k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、boosting方法和条件随机场等. 判别模型利用正负例和分类标签, 关注在判别模型的边缘分布.

判别方法的特点:

• 判别方法寻找不同类别之间的最优分类面, 反映的是异类数据之间的差异.
• 判别方法利用了训练数据的类别标识信息, 直接学习的是条件概率 $P(Y|X)$, 直接面对预测, 往往学习的准确率更高.
• 由于直接学习条件概率 $P(Y|X)$, 可以对数据进行各种程度上的抽象, 定义特征并使用特征, 因此可以简化学习问题.
• 缺点是不能反映训练数据本身的特性.

3.2 Generative Model

生成式模型求得 $P(Y,X)$, 对于未见示例 $X$, 你要求出 $X$ 与不同标记之间的联合概率分布, 然后大的获胜, 如上图右边所示, 并没有什么边界存在, 对于未见示例 (红三角), 求两个联合概率分布 (有两个类), 比较一下, 取那个大的.

这样的方法之所以成为生成方法, 是因为模型表示了给定输入X产生输出Y的生成关系. 用于随机生成的观察值建模, 特别是在给定某些隐藏参数情况下. 典型的生成模型有: 朴素贝叶斯法、马尔科夫模型、高斯混合模型. 这种方法一般建立在统计学和Bayes理论的基础之上.

生成方法的特点:

• 从统计的角度表示数据的分布情况, 能够反映同类数据本身的相似度.
• 生成方法还原出联合概率分布, 而判别方法不能.
• 生成方法的学习收敛速度更快, 即当样本容量增加的时候, 学到的模型可以更快地收敛于真实模型.
• 当存在隐变量时, 我们仍可以用生成方法学习, 此时判别方法不能用.

3.3 Comparison

假设有四个samples:

	sample 1	sample 2	sample 3	sample 4
x	0	0	1	1
y	0	0	0	1

判别式模型的世界是这样的: $\sum P(y|x)=1$

	y=0	y=1
x=0	1	0
x=1	1/2	1/2

生成式模型的世界是这样的: $\sum P(x,y)=1$

	y=0	y=1
x=0	1/2	0
x=1	1/4	1/4

注:

生成模型对联合概率分布建模, 判别模型对条件概率分布建模. 生成模型有更高的泛化能力和普适性, 也就意味着更高的计算复杂度, 他能帮助发现数据中新的特性. 判别模型相对来说直男一点, 你让他干点啥, 他就只干点啥. 就信息量来讲, 很明显上图生成模型的信息量是高于下图判别模型的信息量的.

4. Bayes Decision Theory

对于分类任务来说, 在所有相关概率都已知的理想情形下, 贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记.

假设有 $N$ 种可能的类别标记, 即 $\mathcal{Y}=\{c_1,c_2,…,c_N\}$, $\lambda_{ij}$ 是将一个真实标记为 $c_j$ 的样本误分类为 $c_i$ 所产生的损失, 基于后验概率 $P(c_i|x)$ 可获得将样本 $x$ 分类为 $c_i$ 所产生的期望损失 (expected loss), 即所有损失的平均值

$$R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x)$$

上面这个式子是针对单个样本 $x$ 的, 而下面这个式子是针对整个数据集 $D$ 所有样本的期望, 即

$$R(h)=\mathbb{E}_x[R(h(x)|x)]=\mathop{\sum}\limits_{x\in D}R(h(x)|x)P(x)$$

其中 $P(x)$ 为样本 $x$ 出现的概率, 且满足 $\sum_{x\in D}P(x)=1$; $h(x)$ 为判定标准 $h:\mathcal{X}→\mathcal{Y}$ 对样本 $x$ 预测的类别标记; 则 $R(h)$ 表示判定标准 $h$ 的总体风险. 显然如果对每个样本 $x$, 我们能最小化期望损失, 那么总体风险也将最小化. 这就产生了贝叶斯判定准则 (Bayes Decision Rule):

$$h^*(x)=\arg\min R(c|x),c\in\mathcal{Y}$$

具体来说, 如目标是最小化分类错误率, 则误判损失 $\lambda_{ij}$ 可写为

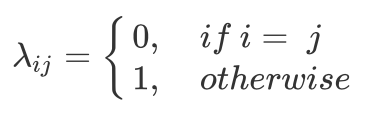
此时单个样本的期望损失为

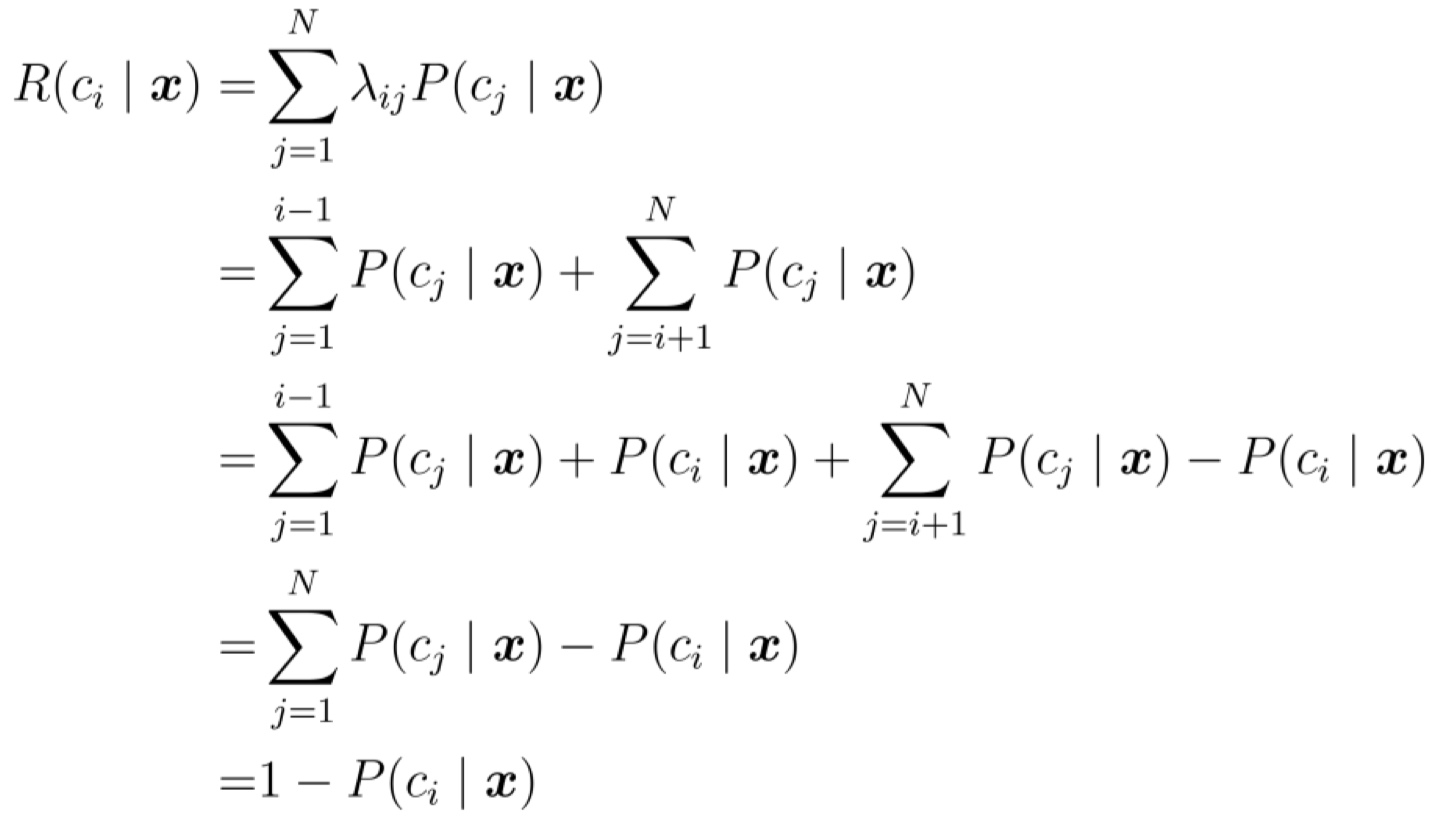
于是, 最小化分类错误率的贝叶斯最优分类器为

$$h^*(x)=\arg\max P(c|x),c\in\mathcal{Y}$$

然而在现实任务中, 我们很难直接获得后验概率 $P(c|x)$. 从这个角度来看, 机器学习所要实现的是基于有限的训练样本集尽可能准确地估计后验概率 $P(c|x)$. 大体来说, 主要有两种策略:

• 判别式模型 (Discriminative Models)

  给定 $x$, 可通过直接建模 $P(c|x)$ 来预测 $c$.

• 生成式模型 (Generative Models)

  先对联合概率分布 $P(x,c)$ 建模, 然后再由此获得 $P(c|x)$. 数学表达式即是

  $$P(c|x)=\frac{P(x,c)}{P(x)}$$

  基于贝叶斯定理, $P(c|x)$ 可写为

  $$P(c|x)=\frac{P(x|c)P(c)}{P(x)}$$

  其中, $P(c)$ 是类先验概率 (Prior), $P(x|c)$ 是样本 $x$ 相对于类标记 $c$ 的类条件概率 (class-conditional probability), 或称为似然 (likelihood). $P(x)$ 是用于归一化的证据因子, 对于给定样本 $x$, 证据因子 $P(x)$ 与类别标记无关. 因此, 估计 $P(c|x)$ 的问题就转换为如何基于训练数据 $D$ 来估计先验概率 $P(c)$ 和似然 $P(x|c)$.

  对于似然 $P(x|c)$, 我们很难直接按频率去估计. 因为, 假设样本有 $d$ 个属性都是二值的, 则样本空间将有 $2^d$ 种可能的取值, 而在现实中, 这个值往往远大于训练样本数 $m$, 也就是说, 很多样本取值在训练集中根本没有出现. 因此直接使用频率来估计 $P(x|c)$ 是不可行的, 因为未被观测到与出现概率为零通常是不同的.

5. Naive Bayes

基于贝叶斯公式来估计后验概率 $P(c|x)$ 的主要困难在于: 似然概率 $P(x|c)$ 是==所有属性上的联合概率==, 难以从有限的训练样本中直接估计而得.

因此, 为了避开这个障碍, 朴素贝叶斯分类器 (Naive Bayes Classifier) 采用了属性条件独立性假设 (attribute conditional independence assumption): 对已知类别, 假设所有属性相互独立. 换句话说, 假设每个属性独立地对分类结果产生影响.

我们知道, 此假设通常是不成立的, 不过这并不影响我们使用它, 因为它带来的计算简化效果远远超过了打破假设的理论损失.

因此, 尽管有这些相当乐观的假设, 但朴素的贝叶斯分类器通常胜过更复杂的选择. 尽管各个类别的密度估计可能存在偏差, 但这种偏差可能不会对后验概率造成太大的损失, 尤其是在决策区域附近.

基于此假设, 贝叶斯公式可以重写为

$$P(c|x)=\frac{P(x|c)P(c)}{P(x)}=\frac{P(c)}{P(x)}\prod_{i=1}^dP(x_i|c)$$

由于对于同一样本而言 $P(x)$ 是相同的, 因此最优化贝叶斯分类器可以写为

$$h_{ab}(x)=\arg\max P(c)\prod_{i=1}^dP(x_i|c),c\in\mathcal{Y}$$

这就是大名鼎鼎的朴素贝叶斯分类器的表达式. 很显然, 朴素贝叶斯分类器的训练过程分过两个大步骤:

1. 基于训练集 $D$ 来估计类先验概率 $P(c)$

   $$P(c)=\frac{|D_c|}{D}$$

2. 并为每个属性估计条件概率 $P(x_i|c)$

   • 对于离散属性我们可以按以下方式计算

     $$P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}$$

   • 对于连续属性我们可以考虑概率密度函数, 假定 $p(x_i|c)\sim\mathcal{N}(\mu_{c,i},\sigma_{c,i}^2)$, 则有

     

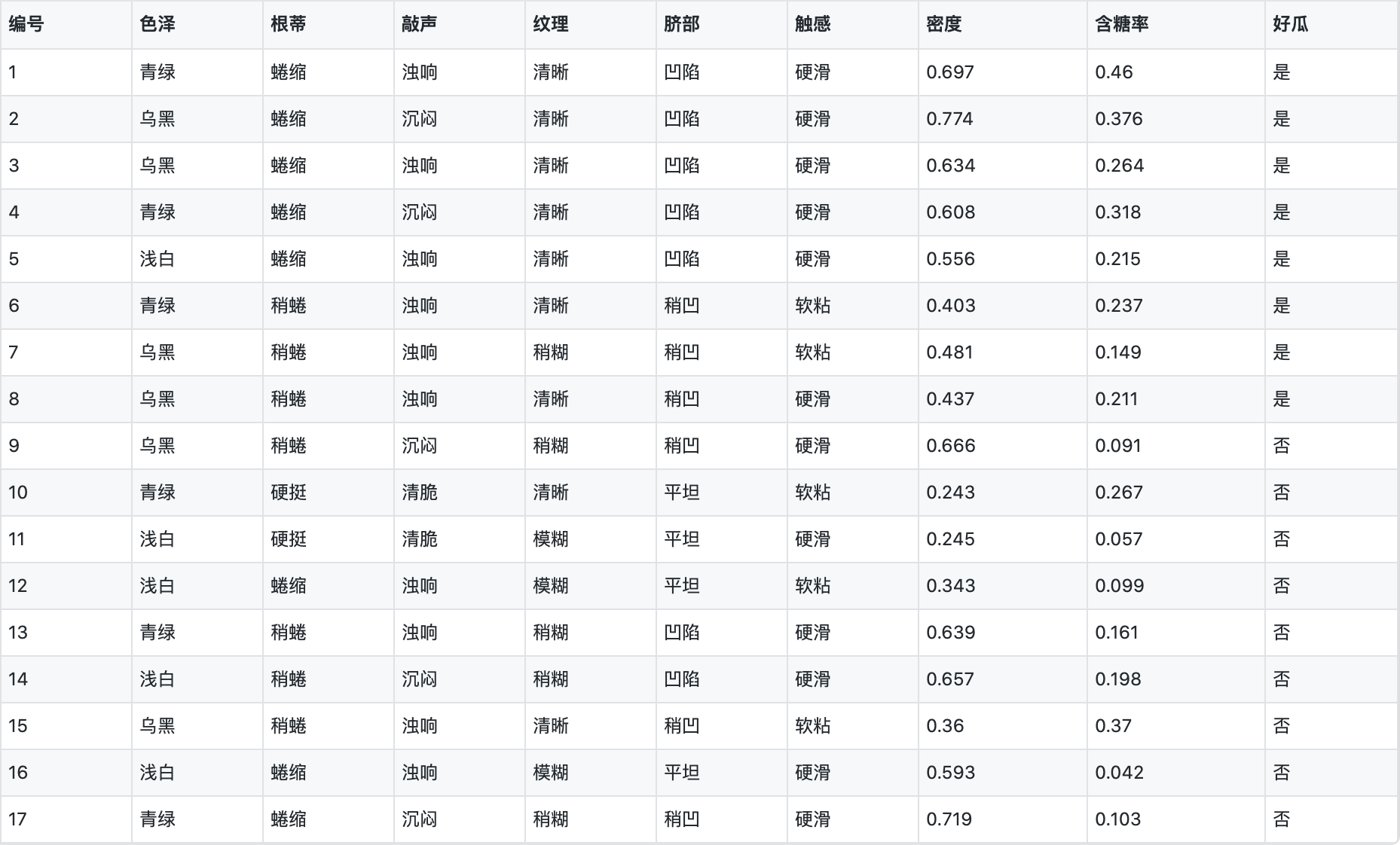
我们用下面这个数据集来训练一个分类器, 并对测试例进行分类

训练集:

测试例:

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
测 1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	?

Step 1: 估计类先验概率 $P(c)$, 显然有

Step 2: 为每个属性估计条件概率 $P(x_i|c)$

Step 3: 计算结果

因此, 朴素贝叶斯分类器将测试样本判别为好瓜.

但需要注意, 有些时候我们可能会出现条件概率为零的情况. 打个比方, 对于上述数据集

这会导致连乘式计算出的概率值为零 (虽然实践中我们通常使用取对数的方式来将连乘转换为连加以避免数值下溢), 进而导致分类器失效. 为了避免这种情况的出现, 我们在估计概率值的时候通常要进行平滑 (smoothing).

平滑有很多种方法, 我们在这里主要介绍拉普拉斯修正 (Laplace Correction). 如果你想了其他修正方法, 可以参考我的 NLP 笔记.

拉普拉斯平滑

令 $N$ 表示训练集 $D$ 中可能的类别, $N_i$ 表示第 $i$ 个属性可能的取值数, 则修正后的类先验概率和每个属性估计条件概率可表示为

$$\hat{P}(c)=\frac{|D_c|+1}{|D|+N}$$ $$\hat{P}(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}$$

6. Bayes Network

我们首先要介绍一下什么是概率图模型.

概率图模型是用图来表示变量概率依赖关系的理论, 结合概率论与图论的知识, 利用图来表示与模型有关的变量的联合概率分布.

如果用一个词来形容概率图模型（Probabilistic Graphical Model）的话, 那就是“优雅”. 对于一个实际问题, 我们希望能够挖掘隐含在数据中的知识. 概率图模型构建了这样一幅图, 用观测结点表示观测到的数据, 用隐含结点表示潜在的知识, 用边来描述知识与数据的相互关系, 最后基于这样的关系图获得一个概率分布, 非常“优雅”地解决了问题.

概率图中的节点分为隐含节点和观测节点, 边分为有向边和无向边. 从概率论的角度, 节点对应于随机变量, 边对应于随机变量的依赖或相关关系, 其中有向边表示单向的依赖, 无向边表示相互依赖关系.

概率图模型分为贝叶斯网络（Bayesian Network）和马尔可夫网络（Markov Network）两大类. 贝叶斯网络可以用一个有向图结构表示, 马尔可夫网络可以表示成一个无向图的网络结构. 更详细地说, 概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等, 在机器学习的诸多场景中都有着广泛的应用.

6.1 Introduction

对于任意的随机变量, 其联合概率可由各自的局部条件概率分布相乘而得出:

$$P(x_1,x_2,...,x_k)=P(x_k|x_1,...,x_{k-1})...P(x_2|x_1)P(x_1)$$

贝叶斯网络 (Bayesian network), 又称信念网络 (Belief Network), 或有向无环图模型 (Directed Acyclic Graphical Model), 是一种概率图模型, 于1985年由Judea Pearl首先提出. 它是一种模拟人类推理过程中因果关系的不确定性处理模型, 其网络拓朴结构是一个有向无环图 (DAG).

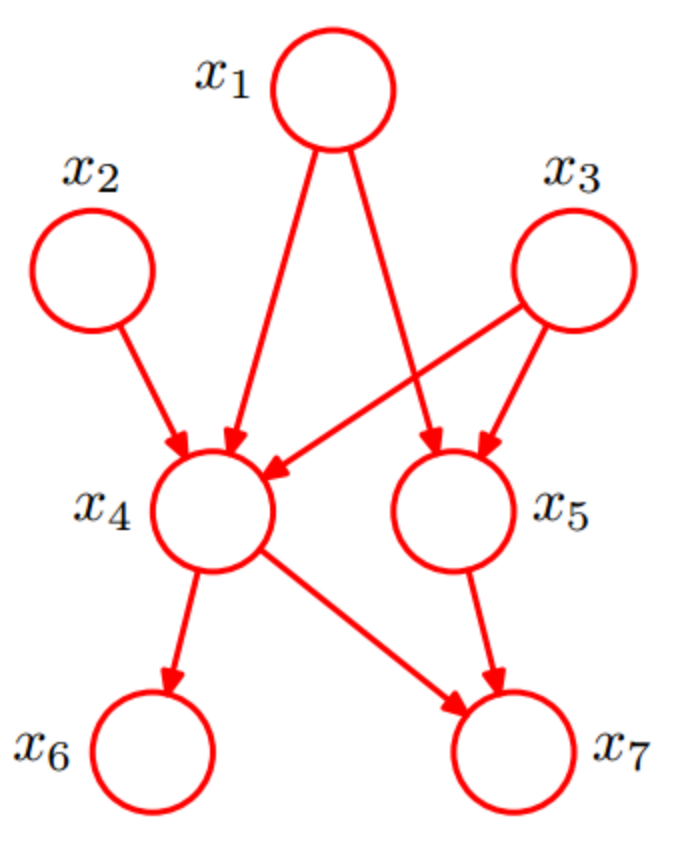
贝叶斯网络的有向无环图中的节点表示随机变量 ${X_1,X_2,…,X_n}$. 它们可以是可观察到的变量, 或隐变量, 未知参数等. 认为有因果关系（或非条件独立）的变量或命题则用箭头来连接. 若两个节点间以一个单箭头连接在一起, 表示其中一个节点是“因(parents)”，另一个是“果(children)”, 两节点就会产生一个条件概率值.

简言之, 把某个研究系统中涉及的随机变量, 根据是否条件独立绘制在一个有向图中, 就形成了贝叶斯网络. 其主要用来描述随机变量之间的条件依赖, 用圈表示随机变量 (random variables), 用箭头表示条件依赖(conditional dependencies).

对于任何贝叶斯网络, 其所代表的联合概率可以表示为:

$$P(\bold{x})=\prod_{i=1}^KP(x_i|pa_i)$$

因此上图的联合概率可以表示为:

$$P(x_1)P(x_2)P(x_3)P(x_4|x_2,x_3)P(x_5|x_1,x_3)P(x_6|x_4)P(x_7|x_4,x_5)$$

我们可以发现, 这和我们最开始所说的联合概率可由各自的局部条件概率分布相乘而得出的结果不一样, 这是因为 A graph not fully connected contains independency assumptions. 上式是化简后的结果.

我们再看一下 A graph fully connected 的例子:

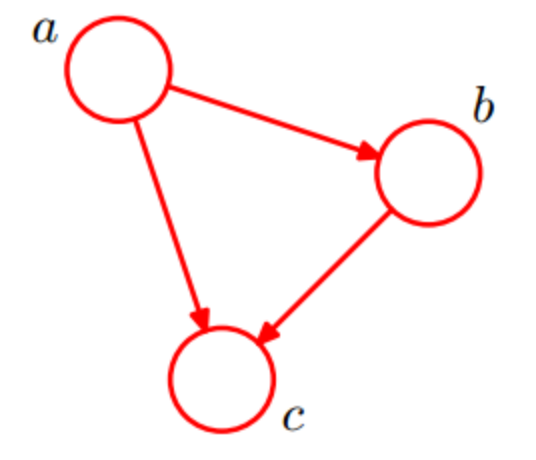
因为 a 导致 b, a和b导致c, 所以有:

$$P(a,b,c)=P(c|a,b)P(b|a)P(a)$$

所以, Fully connected graphs contain no independcy assumption.

6.2 D-Separation

Graphical models allow to directly verify independency assumptions through the d-separation criterion.

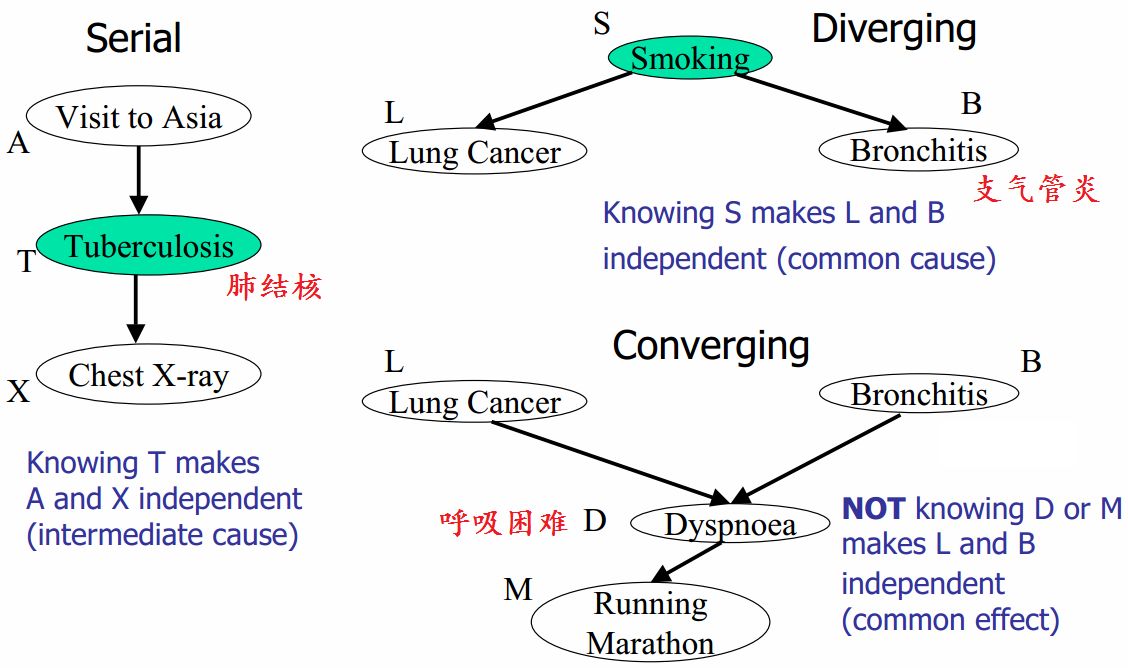
1. Head-to-Head

   

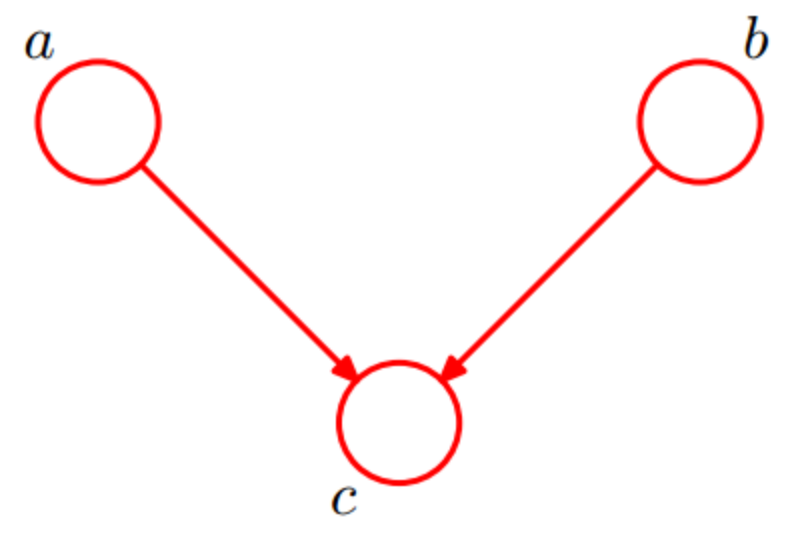
   • Joint distribution:

     $P(a,b,c)=P(c|a,b)P(a)P(b)$

   • a and b are conditionally independent:

     $P(a,b)=\mathop{\sum}\limits_{c}P(c|a,b)P(a)P(b)=P(a)P(b)$

   • a and b are not conditionally independent given c:

     $P(a,b|c)=\frac{P(c|a,b)P(a)P(b)}{P(c)}\ne P(a|c)P(b|c)$

   所以在 $c$ 未知的条件下, a和b被阻断(blocked), 是独立的, 称之为head-to-head条件独立.

2. Tail-to-Tail

   

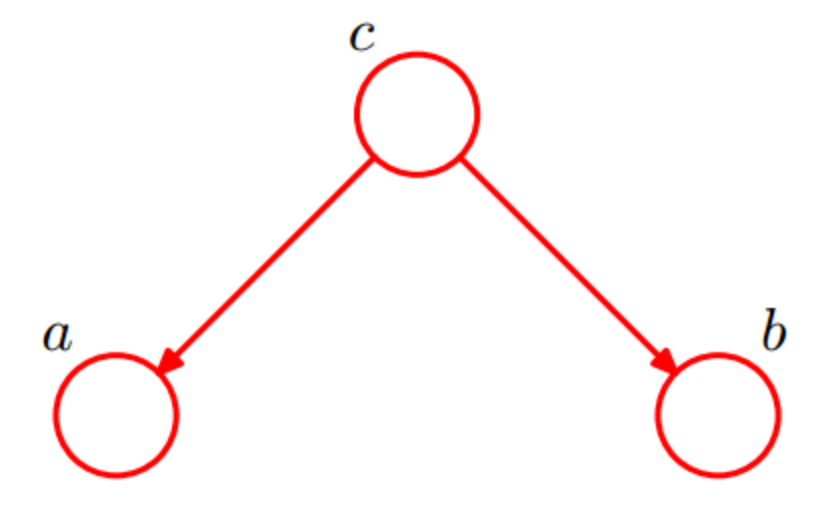
   • Joint distribution:

     $P(a,b,c)=P(a|c)P(b|c)P(c)$

   • a and b are not conditionally independent:

     $P(a,b)=\mathop{\sum}\limits_{c}P(a|c)P(b|c)P(c)\ne P(a)P(b)$

   • a and b are conditionally independent given c:

     $P(a,b|c)=\frac{P(a,b,c)}{P(c)}=P(a|c)P(b|c)$

   即在 $c$ 给定的条件下, a和b被阻断(blocked), 是独立的, 称之为tail-to-tail条件独立.

3. Head-to-Tail

   

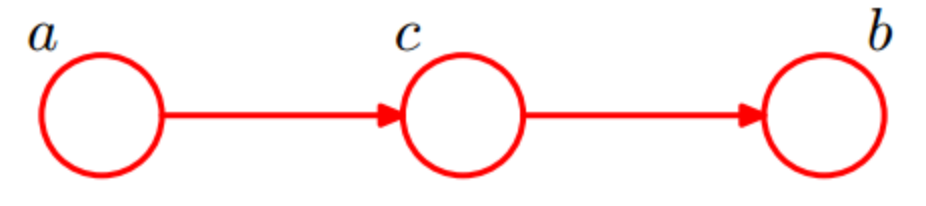
   • Joint distribution:

     $P(a,b,c)=P(a)P(c|a)P(b|c)=P(c)P(a|c)P(b|c)$

   • a and b are not conditionally independent:

     $P(a,b)=P(a)\mathop{\sum}\limits_{c}P(b|c)P(c|a)\ne P(a)P(b)$

   • a and b are conditionally independent given c:

     $P(a,b|c)=\frac{P(b|c)P(a|c)P(c)}{P(c)}=P(b|c)P(a|c)$

   即在 $c$ 给定的条件下, a和b被阻断(blocked), 是独立的, 称之为head-to-tail条件独立.

   插一句, 这个head-to-tail其实就是一个链式网络, 如下图所示：

   

   在 $x_i$ 给定的条件下, $x_{i+1}$ 的分布和 $x_1,x_2,…,x_{i-1}$ 的分布条件独立. 即: $x_{i+1}$ 的分布状态只和 $x_i$ 有关, 和其他变量条件独立, 这种顺次演变的随机过程, 就被称为马尔可夫链 (Markov Chain), 且有:

   $$P(X_{n+1}=x|X_0,X_1,X_2,...,X_n)=P(X_{n+1}=x|X_n)$$

接着, 将上述结点推广到结点集, 则是: 对于任意的结点集 $A,B,C$, 考察所有通过 $A$ 中任意结点到 $B$ 中任意结点的路径, 若要求 $A,B$ 条件独立, 则需要所有的路径都被阻断(blocked), 即满足下列两个前提之一:

• A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C;
• 和B的“head-to-head型”路径不通过C以及C的子孙;

最后, 举例说明上述D-Separation的3种情况, 则是如下图所示: